新的历史时期，我国对内河水运提出了新的要求，水运必须为实施长江经济带等国家战略提供有力支撑，为建设交通强国、调整运输结构、促进经济高质量发展发挥更大作用。目前，金沙江下游水电梯级建设为发展水运创造了有利条件，但在该地区高山峡谷复杂条件下建设通航建筑物的难度较大，限制了黄金水道向上游进一步延伸^[1]。另外，随着我国内河航运高速发展，部分已建通航建筑物的通过能力已不能满足日益增长的货运需求。通航隧洞由于其制约条件少、环境友好和投资造价小等优势，成为解决高山峡谷地区和改扩建通航建筑物布置难题的有效途径之一。

通航隧洞为典型的浅水狭窄型航道，船舶、水体、洞室三者相互制约，在进行隧洞断面尺度分析时需要考虑多因素的影响。一般地，通航隧洞这类限制性航道断面尺度可认为与船舶航速、航行阻力、船艉下沉等船舶航行特性具有高度的相关性^[2-3]，即：航道断面尺度越小，船舶允许航速越小，航行阻力越大。从船舶航行特性的角度来看，通航隧洞断面尺度越大，则船舶航行条件越优越；但是从通航隧洞结构本身来看，隧洞断面尺度越小，其建设难度、对环境的影响和投资造价越小，洞室稳定性也更高。因此，通航隧洞断面尺度设计可以看作是一个多目标优化问题，该问题的最优解是在满足船舶安全航行要求的条件下做到断面尺度最小。

通航隧洞断面尺度主要包括断面系数$n$、断面宽度${B_{\rm{c}}}$、最小航道水深${h_{\rm{c}}}$、水位变幅H₀和通航净高${h_1}$。根据《内河通航标准》(GB 50139—2014)^[2]第3.0.5条的要求，限制性航道的断面系数$n$不应小于6。显然，该标准主要适用于双线通航的限制性航道，对于大型通航隧洞这类单线通航的限制性航道来讲，该要求会导致隧洞开挖量巨大，并随之带来一系列环境和施工问题。另外，通航隧洞内船舶航速较小，而且不存在影响船舶航行状态的风浪，根据目前已建或拟建的通航隧洞断面系数来看（表1），规范中针对双线通航限制性航道规定的断面系数在推广运用到通航隧洞中时，仍有一定的优化空间。

表  1  已建的通航隧洞断面系数

Table  1.  Cross-section coefficients of existing navigation tunnels

通航隧洞	通航净宽/m	最小通航水深/m	断面系数
构皮滩枢纽通航隧洞	12	4.0	2.70
富春江通航隧洞	20	3.5	3.24
挪威Stad隧道	23	13.0	< 4.00

下载: 导出CSV 

| 显示表格

通航隧洞断面宽度${B_{\rm{c}}}$一般根据设计船型宽度，并考虑其他功能需求所需的断面宽度来确定。断面系数$n$、断面宽度${B_{\rm{c}}}$、最低航道水深${h_{\rm{c}}}$为3个非独立的相关参数，确定其中2个参数后，第3个参数可以在已知设计代表船型参数情况下确定。水位变幅H₀和通航隧洞通航净高${h_1}$可分别根据洞内设计水位组合及《内河通航标准》(GB 50139—2014)^[2]中对跨河建筑物的要求来确定，因此在该研究阶段可看作是定值。基于以上分析可知，通航隧洞断面尺度优化的关键在于断面系数$n$的优化。目前国内部分学者从不同角度对通航隧洞断面尺度进行了研究^[4-6]，但未见从目标优化角度分析的研究报道。

基于上述思路，本文建立了以通航隧洞断面系数$n$和隧洞宽度${B_{\rm{c}}}$为目标函数的多目标优化数学模型，该模型综合考虑了断面尺度对隧洞内船舶航行特征及通过能力的影响，可为大型通航隧洞断面尺度研究提供参考。

1.   目标优化数学模型

1.1   通航隧洞断面尺度优化目标函数

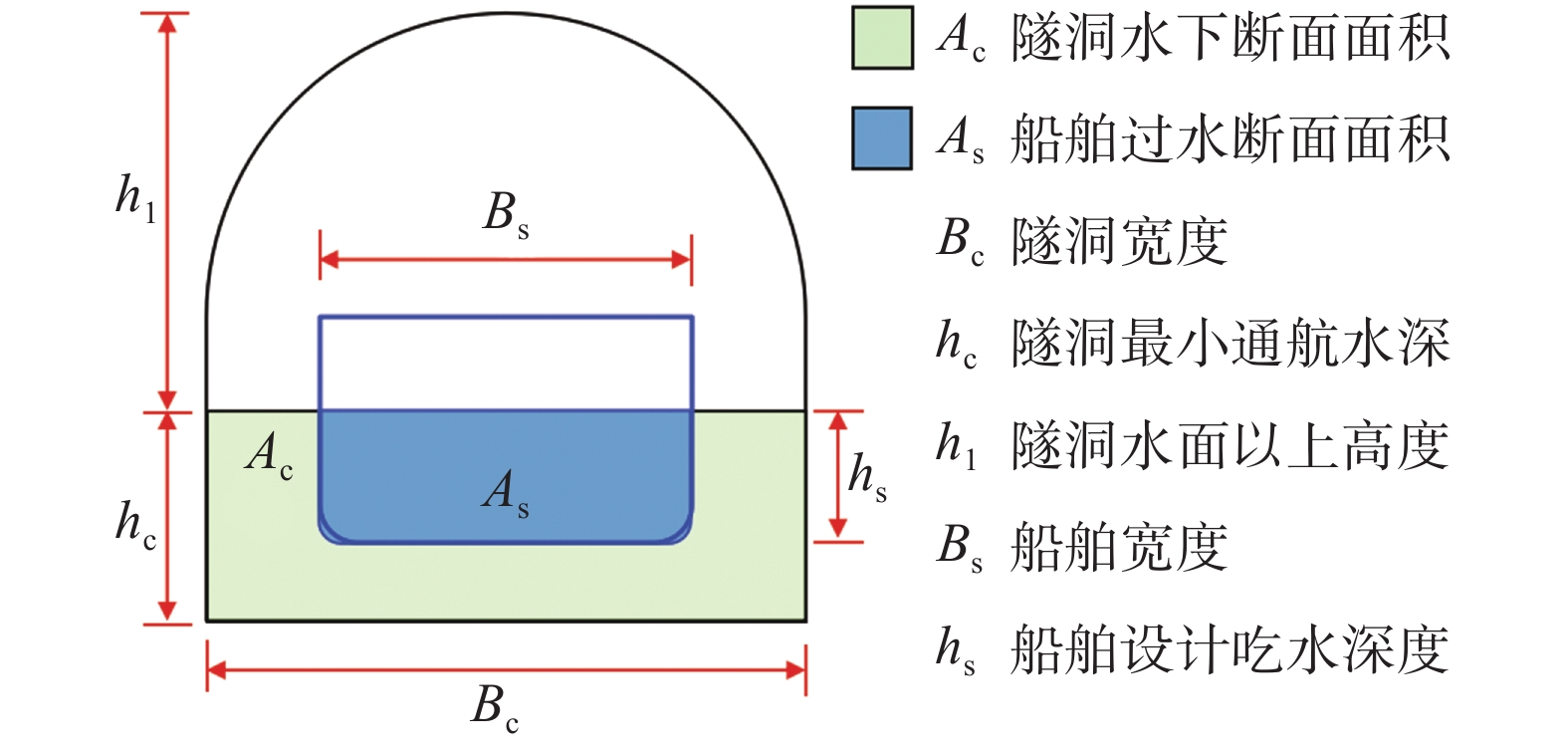
通航隧洞断面系数$n$是与船舶航行特性高度相关的量，其定义为在最小通航水位条件下，隧洞过水断面面积${A_{\rm{c}}}$与船舶舯横剖面浸水面积${A_{\rm{s}}}$之比（见图1）：

图  1  通航隧洞断面尺度参数

Figure  1.  Cross-section dimension parameters of navigation tunnel

下载: 全尺寸图片 幻灯片

式中：${A_{\rm{c}}} = {B_{\rm{c}}} 　{h_{\rm{c}}}$，${B_{\rm{c}}}$为隧洞宽度，${h_{\rm{c}}}$为最低通航水位对应的隧洞最小通航水深；${A_{\rm{s}}}$为设计代表船舶舯横剖面浸水面积。

由于设计代表船型相关参数是在航道规划设计前期就已确定的量，在进行通航隧洞断面尺度分析时可以看作是已知量，因此断面系数$n$可以看作是参数${B_{\rm{c}}}$和${h_{\rm{c}}}$的函数，其一般表达式为：

通航隧洞宽度${B_{\rm{c}}}$的控制因素主要有设计代表船型宽度${B_{\rm{s}}}$、航行漂角$\; \beta $、富裕宽度$\Delta B$，目前国内现行规范对通航隧洞宽度未有明确规定。《内河通航标准》中给出了单线天然和渠化航道宽度及船闸有效宽度的计算公式，本文分析两种计算公式对通航隧洞的适用性，发现单线天然和渠化航道宽度计算公式中考虑了船舶航行漂角对航道宽度设计的影响，而由于船舶进出船闸的速度较小，船闸有效宽度的计算公式中未考虑船舶的航行漂角。但是实际工程中，船舶在通航隧洞中航行速度通常大于船舶进出船闸速度，因此航行漂角的影响不宜忽略。参考单线天然和渠化航道宽度计算公式，通航隧洞宽度${B_{\rm{c}}}$可以表示为：

式中：${L_{\rm{s}}}$为船舶长度，${L_{\rm{s}}}\sin \beta $表征航迹带宽度。《内河通航标准》规定Ⅰ~Ⅴ级航道$\; \beta $可取3°，由于船舶在通航隧洞中航行时不受风浪和水流流速的影响，同时参考已建构皮滩通航隧洞航行漂角取1°的经验，可将航行漂角$\;\beta $的范围设定为1°≤$ \;\beta $≤3°；《内河通航标准》规定$\Delta B$可取(0.34~0.40)${L_{\rm{s}}}\sin \beta $，对于严格控制宽度的通航隧洞来说可取该范围的极小值。由此式（3）可以进一步简化为：

需要指出的是本文的通航隧洞宽度${B_{\rm{c}}}$是指通航净宽，不包括实现其他功能所需要的附加宽度，例如：衬砌厚度、人行道、消防车道或管线廊道布置宽度等。实际上，人行道、消防车道或管线廊道布置宽度等现行规范均有明确规定，隧洞实际开挖宽度可在通航净宽${B_{\rm{c}}}$基础上加上附加宽度即可。

通航隧洞最小通航水深${h_{\rm{c}}}$主要与设计代表船舶吃水深度${h_{\rm{s}}}$和下沉量有关。国内外众多学者对船舶在不同等级航道中的下沉量做了大量研究，并给出了不同适用条件下估算方法^[7-10]。这些估算方法主要针对一般内河限制性航道，对于通航隧洞这类特殊的狭窄型航道来说，在需要加大断面系数满足船舶安全航行要求时，一般建议尽量不加大断面宽度，而是通过增加航道最小通航水深来实现加大断面系数的目的，因此最小通航深度一般满足安全要求，可根据现行规范采用更简捷的估算方法。通航隧洞可以看作是与船闸类似的狭窄型航道，可参照《船闸总体设计规范》（JTJ 305—2001）中对船闸最小闸室水深来设定隧洞最小通航水深${h_{\rm{c}}}$的取值范围：

航道水深对船舶航行的影响主要是当水深较浅时，航道底部限制了绕船舶的水流运动，增加了对船舶的水流速度，从而产生了阻塞效应^[11]。显然，当航道水深达到一定深度后，航道底部对船舶航行的影响可忽略，此时可以称为“深水航道”。因此，可以采用“深水航道”对应的临界值作为隧洞最小通航水深${h_{\rm{c}}}$的上限值。对于“深水航道”的界限目前比较通用的方式是根据水深吃水比${h_{\rm{c}}}/{h_{\rm{s}}}$来确定，根据国际航运协会的建议，“深水航道”对应的水深吃水比${h_{\rm{c}}}/{h_{\rm{s}}}$可以取为3^[12]。因此，通航隧洞最小通航水深${h_{\rm{c}}}$的最终取值范围可以设置为：

式（6）中${h_{\rm{c}}}$的取值范围可以看作是满足船舶安全航行的有效水深。

综合以上分析可得出，通航隧洞断面尺度优化目标函数为：

1.2   通航隧洞断面尺度约束条件

在给出通航隧洞断面尺度优化目标函数后，需要根据约束条件求出最优解。如前文所分析，现行规范未对通航隧洞断面系数$n$给出明确的约束条件，其关于一般限制性航道的要求不能适用于大型通航隧洞，因此需要根据其他与断面系数$n$相关参数的取值要求来间接获得断面系数$n$的约束条件。

通航隧洞内船舶航行阻力$P$是与断面系数$n$高度相关的参数，一般认为船舶在狭窄水道中航行时，航行阻力随着航速${v_{\rm{s}}}$的增加和断面系数$n$的减小而呈非线性增长^[13-16]，并且对于某一给定的限制性航道断面，存在着一个自航船舶所能达到的极限速度，即为Schijf极限速度${F_{{\rm{hL}}}}$^[15]：

由式（9）可以推出船舶在某一给定的限制性航道断面中临界航速${v_{{\rm{s}}\lim }}$^[5]：

可以看出，式（10）中临界航速${v_{{\rm{s}}\lim }}$是自变量为断面系数$n$和最小通航水深${h_{\rm{c}}}$的递增函数，如若能确定临界航速${v_{{\rm{s}}\lim }}$的取值范围，则能反推$n$和${h_{\rm{c}}}$的约束范围。

另一方面，船舶航速${v_{\rm{s}}}$的大小还关系到区域航道规划运力的实现，其在航道规划时具有较高优先级，因此可以根据航道规划设计的通过能力来确定船舶最小航速${v_{{\rm{s}}\min }}$。在确定${v_{{\rm{s}}\min }}$之前需要引入合理的假设条件来简化分析过程：① 通航隧洞一般与引航道、船闸、升船机等通航建筑物相连接，其通过能力不低于枢纽设计水平年过闸需求；②船舶采用单艘、依次、顺序的过洞方式。

基于以上假设，船舶最小平均航速${v_{{\rm{s}}\min }}$可以按下式来确定：

式中：${L_{\rm{c}}}$为与隧洞相连接的中间渠道总长度（m）；${L_{\rm{s}}}$为船舶长度（m）；$d$为前后船舶安全间距（m）；$m$为单闸次船舶数；$t$为通过能力控制性结构（船闸或升船机）一次过闸平均时间（h）。$\Delta t$为船舶系缆、解缆以及停靠等时间，可以根据实际工程中船舶过闸运行调度方式来确定。

一般地，考虑到船舶发动机功耗等因素，船舶的最大航速${v_{{\rm{s}}\max }}$一般不超过临界航速${v_{{\rm{s}}\lim }}$的80%^[5,15]，结合式（10）和式（11）可以得出航速${v_{\rm{s}}}$的取值范围为：

由于${v_{{\rm{s}}\lim }}$为$n$和${h_{\rm{c}}}$的函数，则根据式（12）可以推出通航隧洞断面尺度参数$n$和${h_{\rm{c}}}$的约束条件：

如前文分析，函数${f_3}$是自变量为断面系数$n$和最小通航水深${h_{\rm{c}}}$的递增函数，式（13）取等号的意义可以理解为通航隧洞为满足设计通过能力而需要的最小的断面尺度参数$n$和${h_{\rm{c}}}$。

1.3   目标函数求解

多目标优化求解的关键思路是将多目标优化问题转化为单目标优化问题。本文主要有式（7）和（8）两个非独立的目标函数$\min {f_1}$和$\min {f_2}$，由于隧洞宽度${B_{\rm{c}}}$对施工难度、洞室稳定和工程投资有较大影响，在断面系数$n$小于船舶通过能力要求时，一般建议增加最小通航水深${h_{\rm{c}}}$而不改变隧洞宽度${B_{\rm{c}}}$，因此认为目标函数$\min {f_2}$相对于$\min {f_1}$具有较高的优先级，可以先求解目标函数$\min {f_2}$。

目标函数$\min {f_2}$仅有一个自变量$\beta $，其取值区间为[1°，3°]。由于函数${f_2}$为单调递增函数，所以当自变量$\; \beta $=1°，目标函数$\min {f_2}$有最优解。此时$\min {f_2}$的解可以近似表示为：

需要说明的是，由于目前国内外对大型通航隧洞的研究较少，而且通航隧洞内，船体、水体和洞室三者耦合作用机制较为复杂，因此航行漂角$\;\beta $最小值的取值为1°主要参考了已建构皮滩通航隧洞。

在确定目标函数$\min {f_2}$的最优解后，目标函数$\min {f_1}$则可以进一步简化为：

根据约束函数${f_3}$可知，当不等式（13）取等号时，断面系数$n$有最小值，即为目标函数$\min {f_2}$的最优解。此时，目标函数$\min {f_2}$优化问题转化为下列一元多次非线性函数求解问题：

式中：${v_{{\rm{s}}\min }}$和${B_{\rm{c}}}$分别可根据式（11）和（16）获得；${B_{\rm{s}}}$和${h_{\rm{s}}}$为已知量。求解式（16）可采用数值迭代的方法或直接采用图形法，即：在同一坐标系内分别画出函数${f_4}$和${f_5}$的曲线，两曲线的交点即为最小通航水深${h_{\rm{c}}}$的解。将${h_{\rm{c}}}$的解代入到式（16）中即可求得通航隧洞最优断面系数$n$。

2.   算例验证

乌江构皮滩水电站枢纽工程位于我国西南高山峡谷地区，其通航建筑物是枢纽三大主要建筑物之一，最高通航水头199 m，设计代表船型为500 t级船舶。通航建筑物从上游至下游依次由第一级垂直升船机、第一级中间渠道（通航明渠、通航隧洞、通航渡槽）、第二级垂直升船机、第二级中间渠道（通航明渠、通航渡槽）和第三级垂直升船机组成。设计代表船舶长度${L_{\rm{s}}}$为55 m，船宽${B_{\rm{s}}}$为10.8 m，吃水深度${h_{\rm{s}}}$为1.6 m，更多参数详见表2。

表  2  设计代表船型参数

Table  2.  Parameters of designed representative ship

总长/m	水线长/m	垂线间长/m	型深/m	型宽/m	吃水/m	排水体积/m3	方型系数
55.00	53.86	53.00	2.50	10.80	1.60	637.27	0.696
棱型系数	水线面系数	舯剖面系数	浮心纵向位置	首舷弧/m	尾舷弧/m	梁拱/m
0.767	0.853	0.907	0.12	0.34	0.15	0.10

下载: 导出CSV 

| 显示表格

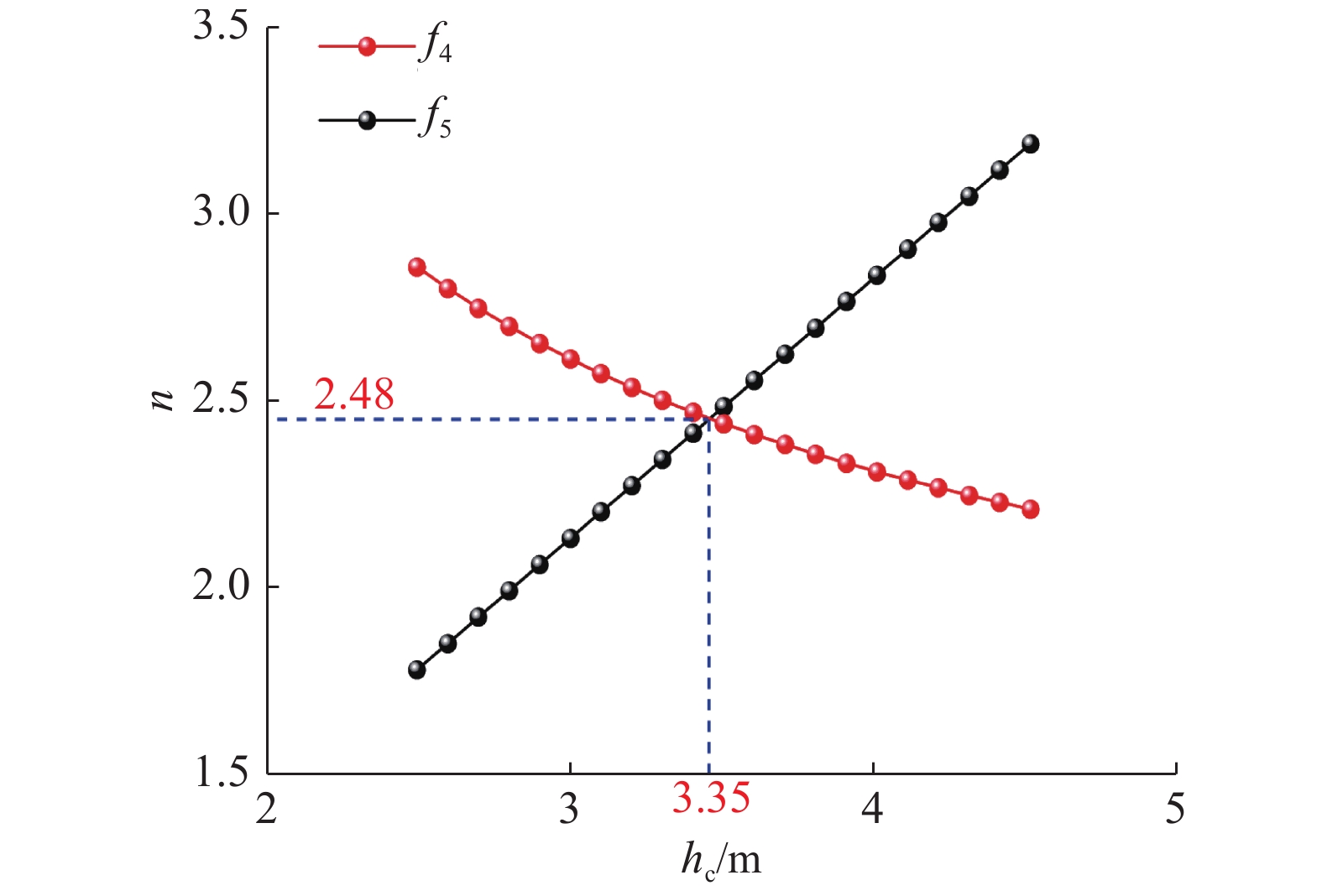
根据式（14）可以确定通航隧洞断面最小宽度$\min {B_{\rm{c}}}$为12.45 m。另外，由于第二级垂直升船机提升高度较大，因此其为船舶通过能力控制性节点。通过对第二级垂直升船机通过能力分析得出，构皮滩通航建筑物年通过能力为149.4万t，日平均过闸次数为39.3次，一次过闸平均时间为33.6 min，单闸次船舶为2艘。第一级中间渠道总长979.5 m，假设船舶在中间渠道船速保持一致，并考虑到船舶解缆、系缆和停靠等时间总共18 min，则根据式（11）可推算出船舶通过隧洞最小航速${v_{{\rm{s}}\min }}$为1.28 m/s。将$\min {B_{\rm{c}}}$和${v_{{\rm{s}}\min }}$代入到式（16）中，并采用图形法可以推导出通航隧洞最小通航水深${h_{\rm{c}}}$为3.35 m，断面系数$n$为2.48（见图2），水深吃水比${h_{\rm{c}}}/{h_{\rm{s}}}$为2.1，满足式（6）中对最小通航水深要求。本文方法计算所得的隧洞通航净宽为12.45 m、最小通航水深为3.35 m、断面系数为2.48，实际工程对应的设计参数分别为12.00 m、4.00 m和2.70，两者相差百分比分别为3.75%，−16.25%和−8.15%。可见两者计算参数相差不大，这证明了本文提出方法的有效性和适用性。

图  2  构皮滩通航隧洞断面系数求解

Figure  2.  Solution to the section coefficient of Goupitan navigation tunnel

下载: 全尺寸图片 幻灯片

3.   工程应用

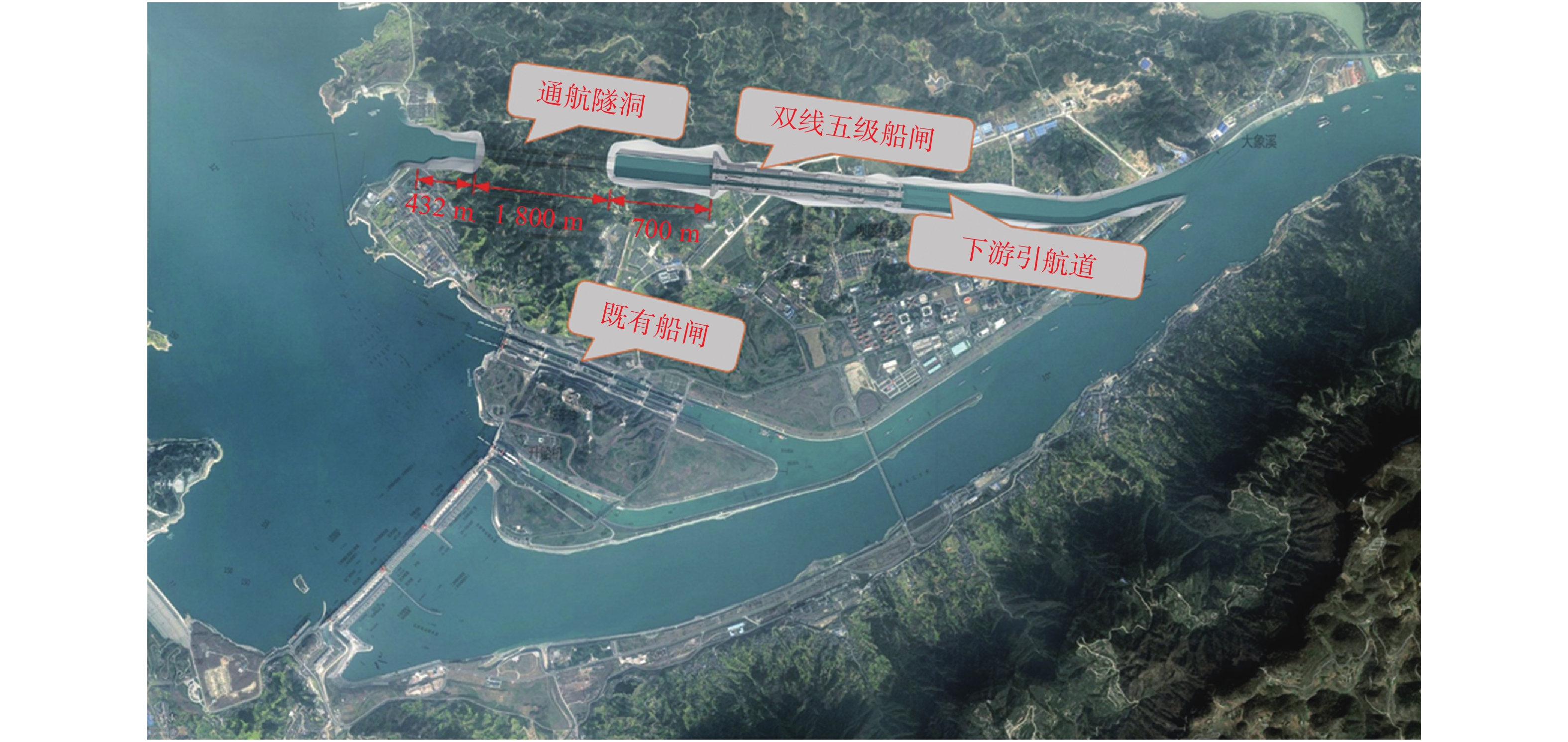
三峡水运新通道左岸线路Ⅳ从上游往下游依次由上游引航道（包括通航隧洞）、双线连续五级船闸和下游引航道组成（见图3），船闸布置在已建三峡船闸北侧偏下游，与已建三峡船闸轴线夹角16°，两者相距2 100~2 600 m。上游引航道为直线航道，总长2 932 m，船闸前为长700 m明挖段，接长1 800 m的通航隧洞跨越驼峰段，后接长432 m明挖段至口门区。下游引航道总长2 007 m，中心线自第6闸首往下游先接长1 111 m直线段，以转弯半径1 000 m向左岸偏转24°后与长江航线衔接。

图  3  三峡水运新通道拟建线路Ⅳ

Figure  3.  Proposed route Ⅳ of the new channel of the Three Gorges Project

下载: 全尺寸图片 幻灯片

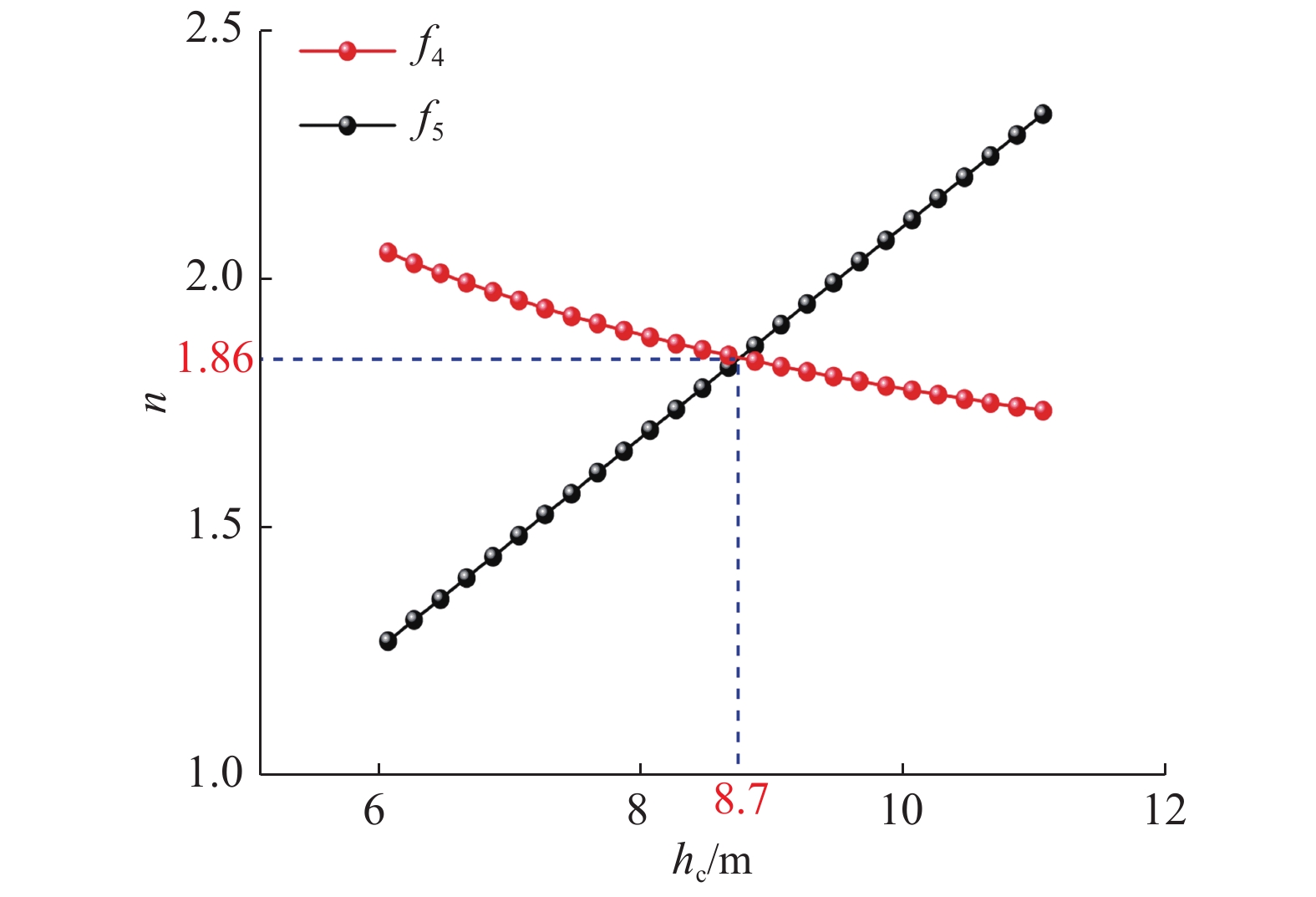
线路Ⅳ通航隧洞按双线双洞布置，仅考虑单船通过。设计代表船型长度${L_{\rm{s}}}$为130 m，宽度${B_{\rm{s}}}$为22 m，吃水深度${h_{\rm{s}}}$为5.5 m。根据三峡水运新通道通过能力要求，新通道船闸日均过闸次数16.62次，日工作23 h，一次过闸平均时间为83.03 min，单闸次船舶按4艘计。为保证通航隧洞通过能力不低于设计过闸要求，则每83.03 min内需要有4艘船舶到达闸前停靠段，另外考虑到船舶系缆、解缆及停靠等各环节时间约30 min，则4艘船舶有效行驶时间为53.03 min。假设船舶在上游引航道内航速一致，由此根据式（11）可知，船舶在隧洞段内最小航速$ {v_{{\rm{s}}\min }} $为1.33 m/s。根据式（14）可以推求出隧洞最小宽度$\min {B_{\rm{c}}}$为25.9 m，将$\min {B_{\rm{c}}}$和${v_{{\rm{s}}\min }}$代入到式（14）中则可推导出通航隧洞最小通航水深${h_{\rm{c}}}$为8.7 m，隧洞断面系数$n$为1.86（见图4），水深吃水比${h_{\rm{c}}}/{h_{\rm{s}}}$约为1.6，通航隧洞最小通航水深基本满足安全航行水深要求（见式（6））。

图  4  三峡水运新通道通航隧洞断面系数求解

Figure  4.  Solution to the section coefficient of the navigation tunnel of the new channel of the Three Gorges Project

下载: 全尺寸图片 幻灯片

4.   结　语

大型通航隧洞断面尺度优化问题的最优解，即是在满足隧洞稳定性和船舶安全航行条件下的断面尺度最小化。本文基于设计通过能力和船舶临界航速，建立了大型通航隧洞断面尺度目标优化数学模型。该模型能够根据隧洞设计通过能力和设计代表船型参数快速有效地分析通航隧洞最优断面尺度，为大型通航隧洞断面尺度设计提供了参考。

大型通航隧洞断面尺度研究既涉及到水力学问题也涉及到洞室结构稳定问题，本文的研究采用了部分现行规范要求，并且参考了已建工程设计参数，简化了研究对象的难度。将在后续的研究中，对船舶、水体、洞室三者相互耦合作用过程进行更为细致的分析。