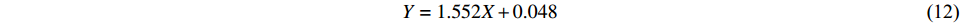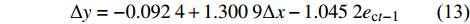Research on interpolation and transfer of cointegration and set pair analysis in rainfall data shortage areas
-
摘要: 针对中小流域降雨资料短缺,洪水精确预报难度大的问题,提出利用线性协整和集对分析(SPA)方法分别对台风雨和非台风雨下的观测降雨数据进行插补移用,以驼英水库为例,进行洪水预报研究。研究得出:(1)基于台风雨协整计算结果发现雨量站之间存在协整关系,协整模拟结果与实测降雨的纳什系数均在0.85以上,相关系数达到0.90,主雨峰和场次降雨误差均较小,说明协整理论可用于降雨资料短缺时的数据插补;(2)非台风雨降雨序列经补充集合经验模态分解(CEEMD)和集对分析(SPA),根据综合联系度拟定数据移用最优方案,显著提高了降雨数据移用的有效性及准确性,提高了洪水预报精度。该方法可为其他同时存在台风雨和非台风雨地区降雨资料的插补移用提供新思路。Abstract: In view of the shortage of rainfall data in small and medium watersheds and the difficulty of accurate flood forecasting, we proposed to use linear cointegration and set pair analysis (SPA) to interpolate and transfer the observational rainfall data under typhoon rain and non-typhoon rain, and carried out the research on flood forecasting of Tuo Ying Reservoir.
The results show that: (1) Based on the typhoon rain cointegration calculation results, it is found that there is a cointegration relationship between rainfall stations. The Nash coefficients of the cointegration simulation results and the measured rainfall are both above 0.85, and the correlation coefficient reaches 0.90. The main rain peak and the raining error are small. The calculation results are good and the integration theory can be used for data interpolation when short of rainfall data. (2) The non-typhoon rain rainfall sequence is decomposed by supplementary ensemble empirical mode (CEEMD) and SPA, and the optimal plan for data migration is drawn up according to the comprehensive connection degree, which significantly improves the effectiveness and accuracy of the migration of rainfall data, and improves flood forecasting accuracy. The method proposed in this paper provides a new idea for the interpolation and transfer of rainfall data in other regions with both typhoon storm and non-typhoon storm. -
洪灾具有破坏性强、影响范围广、突发性强、频率高等特点[1],极易造成社会经济和人民生命财产损失。据统计,洪涝灾害损失在全球所有自然灾害损失中占比高达40%[2]。因此,及时准确的洪水预报作为非工程措施[3],在防洪减灾中发挥着重要作用[4]。洪水预报中,气象数据的可靠性是关键[5],然而降雨资料短缺一直是个难题[6]。因此,插补移用降雨资料是非常必要的[7]。常用的方法有线性相关法、反距离权重法、泰森多边形法及克里金插值法等[8-9]。国内外诸多学者在降雨资料空间插补方面做了大量研究[10-11],但较少考虑降雨序列的非平稳性。随着全球气候变暖,极端降雨事件的频次和强度均发生了变化,变化环境导致极端降雨存在非平稳性[12-13]。台风雨的极端降雨强度大、分布范围广,一定影响范围内的雨量站间的降雨资料存在线性协整关系。因此,考虑降雨数据的线性协整关系并建立模型插补短缺数据,是提高降雨数据插补质量的一种新思路。
因多种因素干扰,降雨序列往往是缺失的[14]。许多学者对无资料地区数据移用进行了研究,通常采用邻近测站资料替代研究区域数据的方法[8],其中,金倩芳[15]分别以卫星降雨数据及测站降雨数据作为驱动建立水文模型,计算结果表明卫星降雨数据驱动的水文预报模型在洪峰预报精度上低于实测降雨数据驱动的模型。可见监测仪器精度不高会降低卫星雷达降雨产品的空间分辨率[16],造成数据精度不高,使得卫星降雨数据驱动的水文预报模型在流域的数据移用方面适用性较差[17]。彭安帮等[18]对流域划分水文相似组并建立子流域洪水预报模型,对无资料地区进行参数移植,模拟中发现在洪水预报精度方面,总体上参数移植后的精度较移植前较差。
无资料地区在降雨数据移用进行流域水文预报时,除需要考虑地形、距离、下垫面等因素做出相似判断外,降雨数据的同一度分析也至关重要。因此,存在由于忽略降雨中心时空分布而造成的数据移用精度不高现象[19-20]。非台风影响下的降雨资料缺少测站引入集对分析(Set Pair Analysis, SPA)[21-22],对相邻站点降雨数据进行确定性和不确定性研究分析,从同、异、反3个角度对降雨序列集合进行定量特性分析测站之间的关联性,可有效提高移用资料的精度。降雨序列是非平稳时间序列,需要寻求一种能从非平稳信号中感受到数据偏差或噪声的数据影响、有效提取具有实际物理意义的特征信号的方法[23],才能准确地进行降雨序列间的集对分析。研究表明,补充集合经验模态(Complementary Ensemble Empirical Mode Decomposition, CEEMD)[24-26]相比于经验模态分解(Empirical Mode Decomposition, EMD)及集合平均经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)不仅解决了模态混叠问题,而且对原始信号进行了精确重构,分解效果更好。利用CEEMD将非台风雨降雨数据分解为多个本征模态函数(Intrinsic Mode Function, IMF)分量,分别建立集对分析,通过综合联系度判别测站之间的相似性,选择最佳降雨数据移用,提高资料移用的准确性,可为无资料地区高精度的洪水预报提供参考依据。
本文针对广西驼英水库洪水预报过程中降雨数据短缺问题,提出一种基于线性协整的台风雨降雨插补和集对分析的非台风雨降雨资料移用方法,以期为洪水预报提供较准确可靠的降雨数据。
1. 研究方法
1.1 线性协整理论
协整分析研究两个及以上非平稳时间序列间的均衡关系,主要步骤包括平稳性检验、协整关系的估计与检验及误差模型的建立,具体步骤见文献[27]。
(1)平稳性检验方法。对时间序列进行平稳性检验,即单位根(Augmented Dickey-Fuller, ADF)检验。ADF检验中最小二乘法回归模型有以下3种:
$$ 有截距有趋势:\qquad\qquad\qquad \Delta {y_t} = \alpha + \beta t + (\rho - 1){y_{t - 1}} + \sum\limits_{i = 1}^k {{\delta _i}\Delta {y_{t - i}}} + {\varepsilon _t}$$ (1) $$ 有截距无趋势:\qquad\qquad\qquad \Delta {y_t} = \alpha + (\rho - 1){y_{t - 1}} + \sum\limits_{i = 1}^k {{\delta _i}\Delta {y_{t - i}}} + {\varepsilon _t} $$ (2) $$ 无截距无趋势: \qquad\qquad\qquad\Delta {y_t} = (\rho - 1){y_{t - 1}} + \sum\limits_{i = 1}^k {{\delta _i}\Delta {y_{t - i}}} + {\varepsilon _t}$$ (3) 式中:
$ \Delta {y_t} $ 为变量y的一阶差分;t为时间项;$\alpha $ 为截距;β为回归系数;$\;\rho $ 为系数;i为时间滞后项;k为滞后阶数(AIC和SC准则确定);$\Delta {y_{t - i}}$ 为滞后i时刻的变量y的一阶差分;${\delta _i}$ 为时间项相关系数;${\varepsilon _t}$ 为白噪声。在零单位根检验时,假设有单位根,若ADF的显著性检验统计量小于相应的置信度(10%,5%,1%),则说明该时间序列为平稳序列,否则对降雨序列先进行一阶差分后再次进行检验,直至降雨序列差分为平稳序列,并判断两个降雨序列的单整阶数。若两个时间序列具有相同的单整阶数,则进行以下的协整关系估计与检验。
(2)协整关系的估计与检验。通过最小二乘法对2个降雨序列进行协整回归,并对回归方程的残差是否具有单位根进行检验。若2个时间序列是协整的,则残差将是平稳的。
(3)误差修正模型建立。若降雨序列间存在协整关系,则可根据两变量的一阶自回归滞后模型建立误差修正模型(Error Correction Model, ECM):
$$ \Delta {y_t} = {\beta _0} + {\beta _1}\Delta {x_t} + \gamma {e_{t-1}} + {\varepsilon _t} $$ (4) 式中:
$\Delta {y_t}$ 、$\Delta {x_t}$ 分别为y、x变量在t时刻的一阶差分;$\;{\beta _0}$ 、$\;{\beta _1}$ 为回归系数;${e_{t-1}}$ 为两序列协整关系的前一时刻计算残差;$\gamma$ 为修正系数,即因变量拉回长期均衡状态的速度。1.2 集对分析(SPA)理论
集合对H(A,B)是指由两个相互关联的集合A和B组成的一对集合。这两个集合的性质包括同一度、差异度和对立度[28],其表达式如下:
$$ \mu = S/N + (F/N)m + (P/N)n $$ (5) 式(5)经简化后可得:
$$ \mu = a + bm + cn $$ (6) 式中:
$\;\mu $ 为集合对的综合联系度;S为同一的个数;F为差异的个数;P为对立的个数;N为特征个数总数;a为同一度;b为差异度;c为对立度;m为差异不确定性系数;n为对立系数;在计算中一般取m=0.5,n=−1。根据综合联系度判断目标站点的场次降雨序列与相邻站点降雨序列的相似性,进行综合联系度高的降雨数据的移用,并非距离近的站点间的降雨数据移用,这在很大程度上取决于降雨的时空分布。
1.3 补充集合经验模态(CEEMD)分解方法
CEEMD算法通过对原始信号加入白噪声,有效消除重构信号中的残留噪声,具体步骤[29-30]如下:
(1)在原始信号中分别加入n种固定比例的高斯白噪声,对加噪的信号进行分解,得到n个IMF,将得到的各IMF进行加总平均得IMF1:
$$ {I_{{\text{M}}{{\text{F}}1}}}\left( t \right) = \frac{1}{N}\sum\limits_{i = 1}^N {{E_1}} \left[ {x\left( t \right) + \varepsilon t{\omega _i}\left( t \right)} \right] $$ (7) 式中:
${I_{{\text{M}}{{\text{F}}1}}}$ 为原信号的第一阶分量;N为分解次数;${\omega _i}\left( t \right)$ 为随机高斯白噪声;${E_1}$ 表示EMD分解结果中第一个模态函数分量。从原始信号中减去IMF1得到一阶残差
${r_1}\left( t \right)$ :$$ {r_1}\left( t \right) = x\left( t \right) - {I_{{\text{MF}}1}}\left( t \right) $$ (8) (2)对残差重构待分解信号重新分解,即可得到原始信号的第二模态函数IMF2:
$$ {I_{{\text{M}}{{\text{F}}2}}}\left( t \right) = \frac{1}{N}\sum\limits_{i = 1}^N {{E_1}} \left[ {{r_1}\left( t \right) + \varepsilon {E_1}\left( {{\omega _i}\left( t \right)} \right)} \right] $$ (9) 式中:
$ {r_1}\left( t \right) + \varepsilon {E_1}\left( {{\omega _i}\left( t \right)} \right) $ 为重构分解信号。对k=2, 3,···,k,分别计算第k阶残差:
${r_k} = {r_{k - 1}} - {I_{{\text{MF}}}}_k$ ,根据式(9)得出$ {r_k}\left( t \right) + \varepsilon {E_k}\left( {{\omega _i}\left( t \right)} \right) $ 的第1个分量,通过对IMF平均得:$$ {I_{{\rm M}{{\rm F}{\left( {k + 1} \right)}}}}\left( t \right) = \frac{1}{N}\sum\limits_{i = 1}^N {{E_1}} \left[ {{r_k}\left( t \right) + \varepsilon {E_k}\left( {{\omega _i}\left( t \right)} \right)} \right] $$ (10) (3)反复迭代,直到残差的极值个数不超过2:
$$ R{\text{ = }}x - \sum\limits_{k = 1}^K {{I_{{\text{MF}}}}_k} $$ (11) 式中:
$R$ 为最终残差值;$K$ 为最终IMF分量数。1.4 SCS-CN洪水预报方法
SCS-CN模型是基于水量平衡方程和两个基本假设建立的[31]。由于其模型结构简单,参数较少,被广泛应用于无资料中小河流的洪水预报中[32-33],详细的洪水预报模型原理和过程见参考文献[4],此处不再赘述。
本文采用绝对误差、相对误差、相关系数和纳什系数4个指标评定模型结果。相关系数用来反映模拟值和实测值之间的线性相关程度,纳什系数可以描述洪水预报过程与实测过程之间的拟合程度。
2. 实例应用
驮英水库位于广西宁明县那堪乡垌中村上游约6 km的珠江流域西江水系明江支流公安河上游河段(图1),流域经纬度范围为21°35′45′′N~21°55′5.9′′N,107°17′7.1′′E~107°34′3.7′′E,流域面积606 km2,属南亚热带季风气候[34]。流域内83.87%面积的土壤为壤土,饱和导水率在1.8~18 mm/h范围内。夏末秋季,受南海及太平洋台风影响,工程区多出现台风雨,且台风雨强度大、雨量集中。
由于特殊的地理位置和气候特征,驮英水库流域降雨分为台风雨和非台风雨2种类型。驮英水库未建前曾设有驮英水文站,水文站目前已停测,存有1987—1999年共计13 年的水文气象资料。驮英水库上游流域已建九特、那驮、板固、叫弄、枯强、潭昔、小平共7个雨量站,各站实测降雨是水库来水预报的重要数据来源,现仅有2012—2018年实测资料。数据的不完整性给洪水预报模型的建立和率定带来了一定挑战。由于台风雨与非台风雨的时空异质性差异较大,采用线性协整理论与SPA法分别对台风雨和非台风雨两种情况下的降雨进行插补移用计算。基于线性协整理论的台风雨选取板固和叫弄站2013年、2014年和2016年的3场降雨资料计算;非台风雨选取那驮、九特、板固站2013年、2015年、2017年和2018年的4场降雨序列进行SPA分析降雨数据移用计算。
2.1 基于线性协整关系的台风降雨计算
由于降雨序列为非平稳序列,台风影响下一定范围内雨量站的原始降雨序列间存在“伪回归”的线性关系。因此,需进行协整分析。首先对降雨序列进行ADF检验,以2013年某场降雨为例,表1为台风雨过程下的流域上游板固站与叫弄站降雨序列的ADF检验结果。从表1可以看出,板固站与叫弄站的AIC及SC值均在无截距无趋势模型达到最小,且两站的降雨经一阶差分后均无单位根,这说明经过一阶差分后的降雨序列成为平稳序列,且都为一阶单整序列。
表 1 板固站及叫弄站降雨序列ADF检验结果Table 1. ADF test results of rainfall series at Bangu Station and Jiaonong Station数据 模型 ADF 临界值 AIC准则 SC准则 检验结果
(有无单位根)显著水平1% 显著水平5% 显著水平10% 原数据 有截距有趋势 1.78/−1.99 −4.47/−4.44 −3.65/−3.63 −3.26/−3.26 7.46/6.42 7.66/6.56 有/有 有截距无趋势 1.64/−1.75 −3.77/−3.77 −3.01/−3.00 −2.64/−2.64 7.04/6.43 7.41/6.53 有/有 无截距无趋势 1.12/−1.14 −2.67/−2.67 −1.96/−1.96 −1.61/−1.61 7.29/6.42 7.34/6.47 有/有 一阶差分 有截距有趋势 4.58/−5.80 −4.47/−4.47 −3.65/−3.65 −3.26/−3.26 7.53/6.57 7.68/6.72 无/无 有截距无趋势 4.48/−5.56 −3.79/−3.79 −3.01/−3.01 −2.65/−2.65 7.49/6.56 7.59/6.66 无/无 无截距无趋势 4.60/−5.70 −2.68/−2.68 −1.96/−1.96 −1.61/−1.61 7.40/6.47 7.45/6.52 无/无 注:“/”前为板固站数据,“/”后为叫弄站数据。 用普通最小二乘法(OLS法)估计上述雨量站两降雨序列的长期均衡方程:
$$ Y = 1.552X + 0.048 $$ (14) 对回归方程的残差进行单位根检验,检验结果见表2。残差平稳性检验按照第1种情形(有截距有趋势)接受原假设、第2种情形(有截距无趋势)接受原假设、第3种情形(无截距无趋势)拒绝原假设的流程说明残差是平稳性序列,从而进一步证明了在该场台风雨影响下板固站与叫弄站的降雨序列满足长期线性协整关系。
表 2 残差序列ADF检验结果Table 2. ADF test results of residual sequence数据 模型 ADF 临界值 AIC准则 SC
准则检验结果 显著水平 1% 显著水平5% 显著水平10% 原数据 有截距有趋势 −1.49 −4.89 −3.83 −3.36 3.82 4.34 接受原假设 有截距无趋势 −2.50 −3.81 −3.02 −2.65 5.44 5.64 接受原假设 无截距无趋势 −4.43 −2.67 −1.96 −1.61 5.05 5.10 拒绝原假设 基于二者的线性协整关系建立ECM误差修正模型,其中,ect−1为两个降雨序列协整关系的前一时刻计算残差,并利用OLS法进行误差修正模型的回归分析:
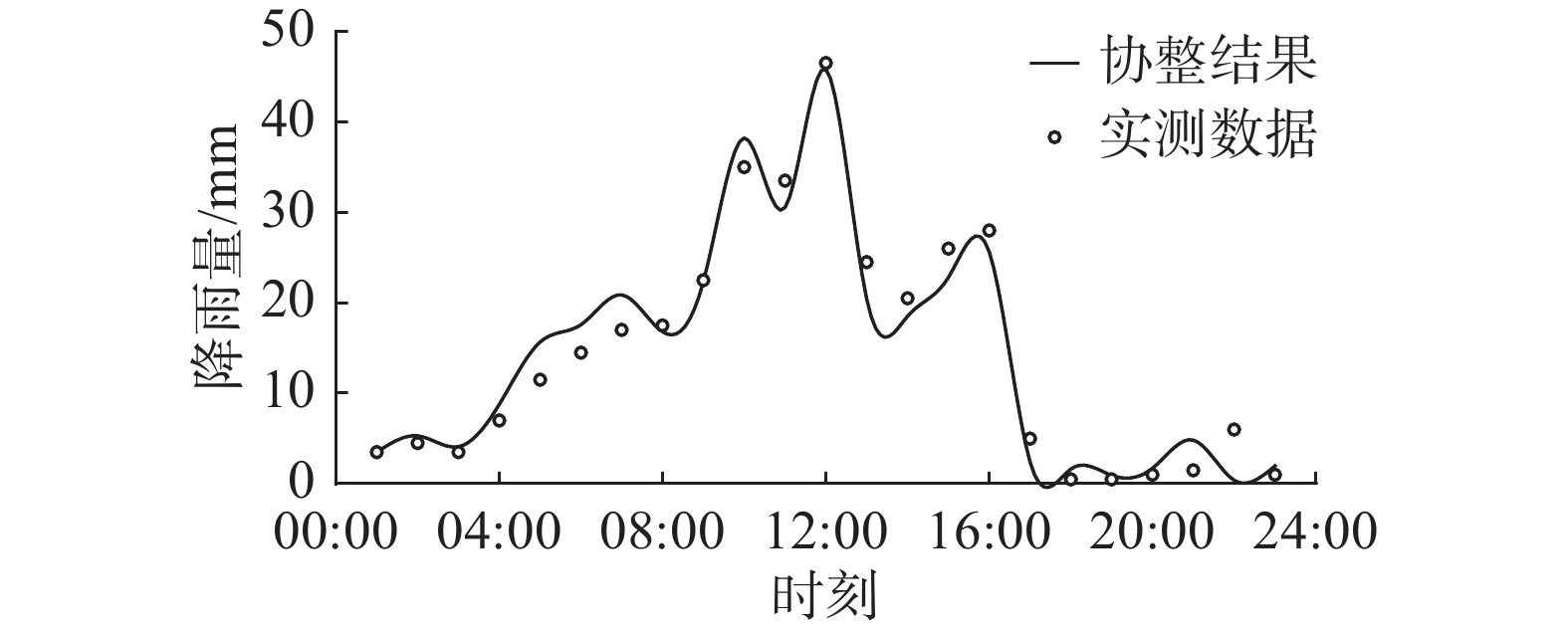
$$ \Delta y = - 0.092\;4 + 1.300\;9\Delta x - 1.045\;2{e_{{\text{c}}{{t - 1}}}} $$ (15) 根据板固站的降雨序列,利用ECM模型计算叫弄站的降雨序列,计算结果见图2。场次雨量峰值的绝对误差为0.7 mm,计算结果和实测降雨的最大绝对误差也仅为4.0 mm,且降雨峰值出现时间相同;计算结果与实测数据的纳什系数为0.901,相关系数为0.979,主雨峰相对误差1.5%,场次降雨总量相对误差0.3%,误差较小满足要求,这表明该方法可以用于降雨序列间的插补计算。
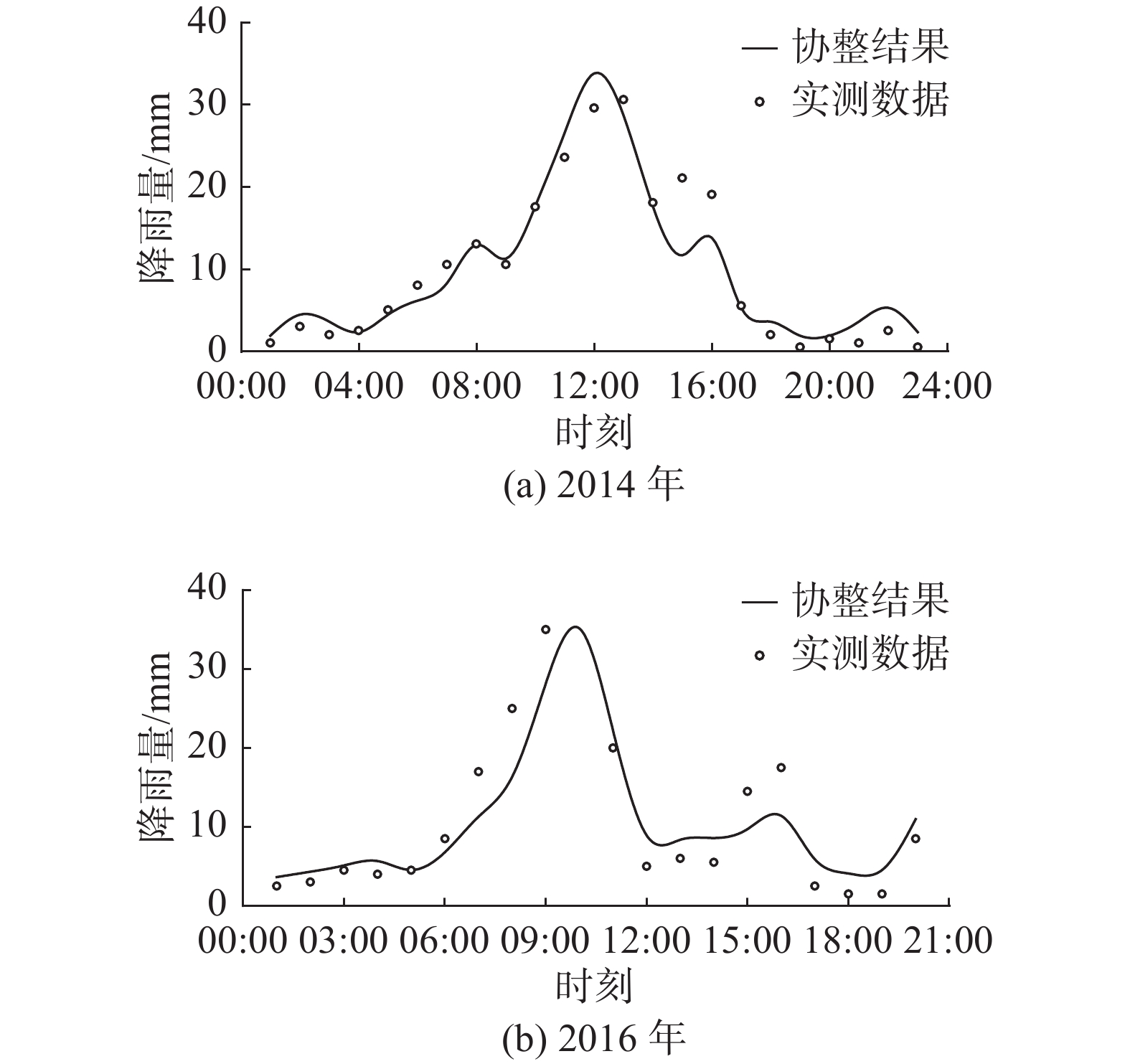
利用协整理论对2014和2016年的两场降雨计算分析,模拟结果见图3。可以看出,总体计算结果较好。2014年场次降雨协整计算结果和实测数据相比,最大绝对误差9.4 mm,纳什系数0.892,相关系数0.955,主雨峰相对误差6.25%,场次降雨总量相对误差8.8%;2016年某场降雨与真实数据对比,最大绝对误差6.9 mm,纳什系数0.886,相关系数0.958,主雨峰相对误差14.69%(实测降雨47.0 mm,模拟降雨40.1 mm),场次降雨总量相对误差8.1%;协整计算雨量与实测数据拟合效果较好。由此可见,雨量信息缺失值可采用测站间协整理论插值得出,提高降雨序列完整性。
2.2 基于SPA的非台风降雨移用
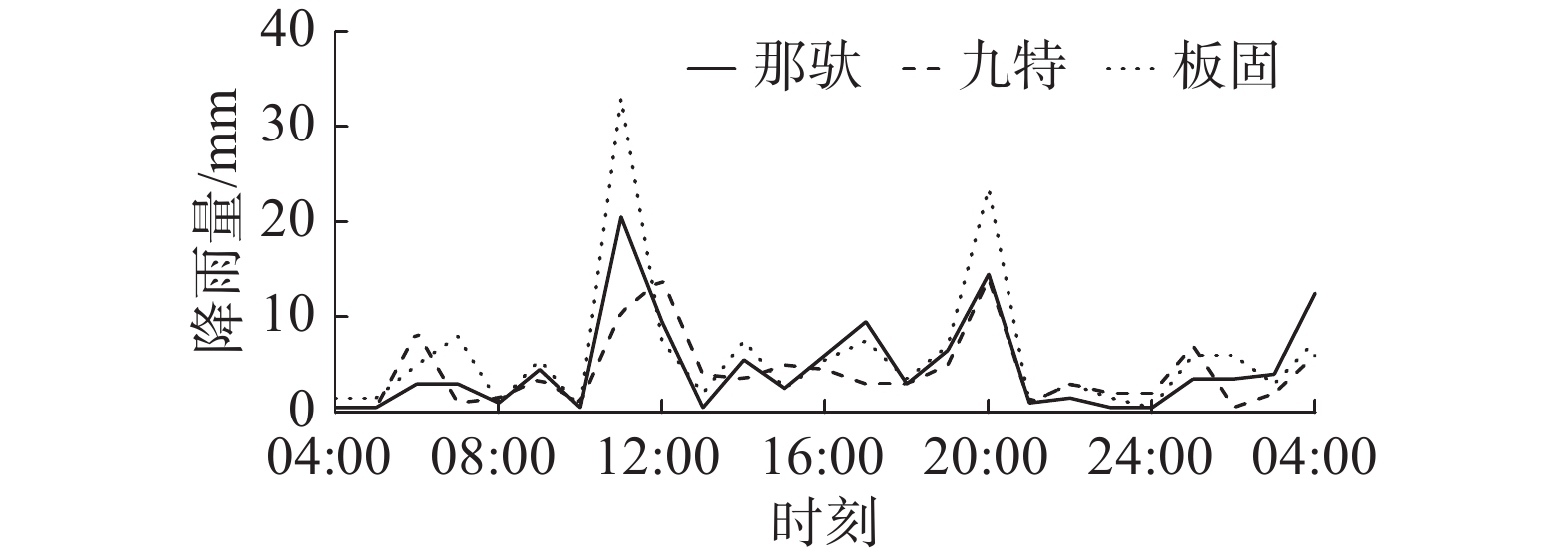
那驮、九特、板固3个雨量站间彼此相邻,2018年某一场降雨实测过程如图4所示。可以看出那驮站的降水峰值处于板固站和九特站之间;该场降雨中,板固站降水峰值时刻更接近那驮站雨量峰值时刻,板固站和那驮站相关系数为0.907,九特和那驮的相关系数为0.725,板固站降雨序列和那驮站的相关性更好。从降水时空分布初步考虑,板固站的降水数据移用到那驮站更为合理。
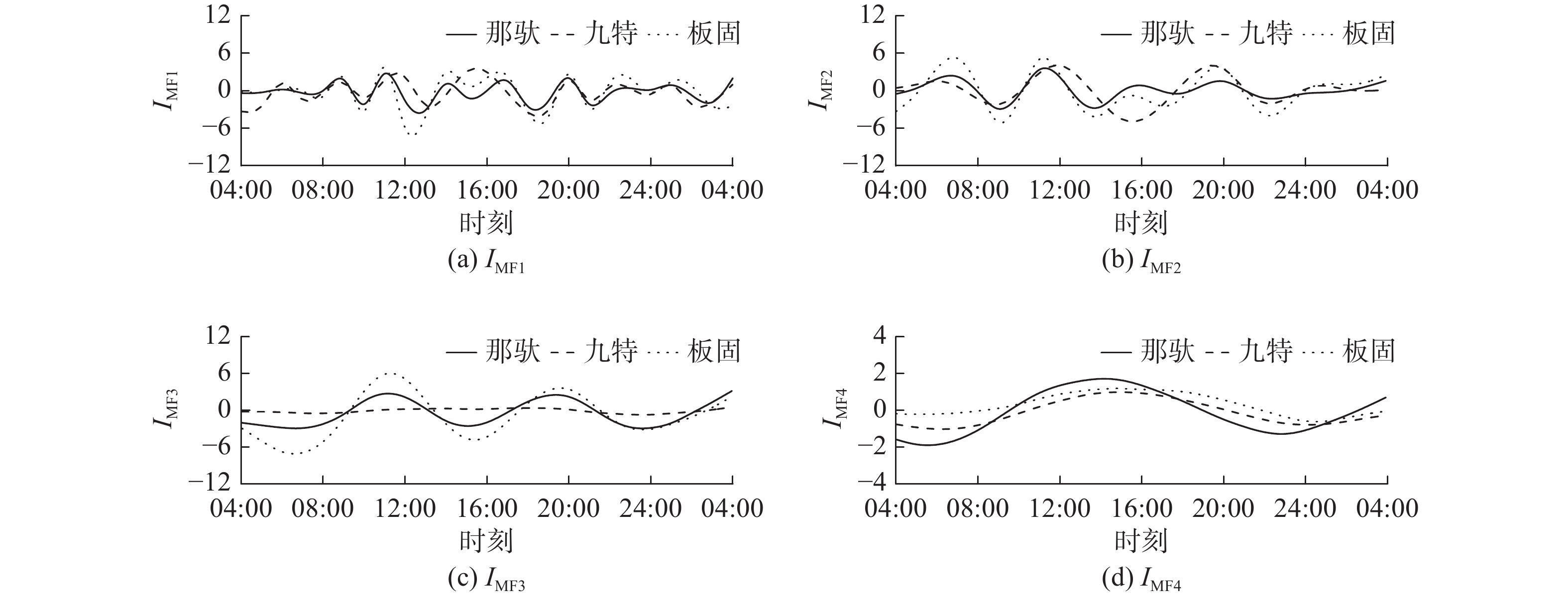
选取非台风雨影响下的那驮、九特、板固站记录的场次降雨序列分别进行CEEMD分解,结果见图5。CEEMD将降雨原序列分解为4个IMF分量,每个IMF的频率、振幅、周期都不同;从IMF1到IMF4频率和振幅变小,周期变长;IMF1和IMF2的振幅和频率较大,周期较短,IMF3和IMF4的振幅和频率较小,周期较长。
每个IMF分量的集对分析结果见表3。从表3可以看出,本场降雨过程中,那驮-九特的同一性较高,而差异性和对立性低于那驮-板固站,具体表现在那驮站-板固站的平均综合联系度0.893,那驮-九特的平均综合联系度0.732,在数据移植时更适合将板固站的资料移用到那驮站。尽管九特站与那驮站的距离更近,但场次降雨相似性在很大程度上取决于降雨的时空分布。
表 3 IMF分量集对分析结果Table 3. Analysis results of IMF component set pairs集对 a b c $ \mu $ 平均 那驮-九特 0.500 0.464 0.036 0.696 0.732 0.500 0.393 0.107 0.590 0.393 0.607 0 0.697 0.893 0.107 0 0.947 那驮-板固 0.714 0.286 0 0.857 0.893 0.786 0.214 0 0.893 0.929 0.071 0 0.964 0.714 0.286 0 0.857 假设将九特站与板固站记录的该场降雨过程分别移植至那驮站,并参与面雨量计算进行洪水预报。建立的SCS-CN模型经率定后纳什系数为0.87,满足预报精度要求,可用于洪水模拟研究。移用数据的预报结果与真实那驮站降雨资料预报结果见图6。结果表明:利用九特站移用的降雨数据的水文预测值与真实数据预测值之间的纳什系数为0.847,自板固站移用数据的模拟结果与真实预报值间的纳什系数为0.905。因此,板固站的移用数据模拟效果好于九特站。在洪峰预测精度上,实测洪峰为563 m3/s,采用板固站移用情况下预测洪峰为591 m3/s,相对误差为4.97%;采用九特站移用情况下洪峰为503 m3/s,相对误差为10.70%。这说明自板固站移用降雨数据更能保证洪峰流量的准确性,可避免因低估洪峰而发生重大生命财产损失。
那驮、板固、九特降雨资料中,存在多场降雨那驮-板固的综合联系度好于那驮-九特的现象。另外,分析了2013年、2015年和2017年3场降雨测站间集对关系。结果表明:2013年那驮-板固的综合联系度为0.863,略好于那驮-九特的综合联系度(0.836);2015年那驮-板固的综合联系度(0.866)明显高于那驮-九特的(0.741);2017年那驮-板固的综合联系度(0.816)略高于那驮-九特的(0.786)。将板固站的降雨资料移用到那驮站作为洪水预报输入,模拟结果都好于九特站移用结果。因此,非台风雨影响下的目标站点降雨资料移用时,提前对相邻站点同时段现有序列分别进行集对分析,根据综合联系度指标衡量移用对象在此场降雨中与目标站降雨序列的相似性,可提高移用数据的可靠性和合理性。
3. 结 语
针对驼英水库洪水预报过程中降雨数据短缺现象,提出了基于线性协整和集对分析分别对台风雨和非台风雨降水序列插补移用,并用此方法对驮英水库进行了洪水预报研究。主要结论如下:
(1)基于线性协整关系的台风雨计算,测站之间满足线性协整关系,协整理论模拟值与实测降雨的纳什系数均在0.85以上,相关系数均大于0.90,绝对误差、主雨峰相对误差和场次降雨总量误差均较小,这表明该方法可以插补降雨序列,提高降雨序列的完整性。
(2)非台风降雨移用采用SPA,各个雨量站经CEEMD分解,将IMF的分量采用集对分析,根据综合联系度计算结果移用最佳的降雨资料,利用移用降雨数据进行洪水预报,其纳什系数达到0.85,洪峰预测值相对误差较小。由此可见,SPA方法为无资料地区降雨数据移用提供了一种新思路。
-
表 1 板固站及叫弄站降雨序列ADF检验结果
Table 1 ADF test results of rainfall series at Bangu Station and Jiaonong Station
数据 模型 ADF 临界值 AIC准则 SC准则 检验结果
(有无单位根)显著水平1% 显著水平5% 显著水平10% 原数据 有截距有趋势 1.78/−1.99 −4.47/−4.44 −3.65/−3.63 −3.26/−3.26 7.46/6.42 7.66/6.56 有/有 有截距无趋势 1.64/−1.75 −3.77/−3.77 −3.01/−3.00 −2.64/−2.64 7.04/6.43 7.41/6.53 有/有 无截距无趋势 1.12/−1.14 −2.67/−2.67 −1.96/−1.96 −1.61/−1.61 7.29/6.42 7.34/6.47 有/有 一阶差分 有截距有趋势 4.58/−5.80 −4.47/−4.47 −3.65/−3.65 −3.26/−3.26 7.53/6.57 7.68/6.72 无/无 有截距无趋势 4.48/−5.56 −3.79/−3.79 −3.01/−3.01 −2.65/−2.65 7.49/6.56 7.59/6.66 无/无 无截距无趋势 4.60/−5.70 −2.68/−2.68 −1.96/−1.96 −1.61/−1.61 7.40/6.47 7.45/6.52 无/无 注:“/”前为板固站数据,“/”后为叫弄站数据。 表 2 残差序列ADF检验结果
Table 2 ADF test results of residual sequence
数据 模型 ADF 临界值 AIC准则 SC
准则检验结果 显著水平 1% 显著水平5% 显著水平10% 原数据 有截距有趋势 −1.49 −4.89 −3.83 −3.36 3.82 4.34 接受原假设 有截距无趋势 −2.50 −3.81 −3.02 −2.65 5.44 5.64 接受原假设 无截距无趋势 −4.43 −2.67 −1.96 −1.61 5.05 5.10 拒绝原假设 表 3 IMF分量集对分析结果
Table 3 Analysis results of IMF component set pairs
集对 a b c $ \mu $ 平均 那驮-九特 0.500 0.464 0.036 0.696 0.732 0.500 0.393 0.107 0.590 0.393 0.607 0 0.697 0.893 0.107 0 0.947 那驮-板固 0.714 0.286 0 0.857 0.893 0.786 0.214 0 0.893 0.929 0.071 0 0.964 0.714 0.286 0 0.857 -
[1] YAN L, CHEN C W, HANG T T, et al. A stream prediction model based on attention-LSTM[J]. Earth Science Informatics, 2021, 14(2): 723-733. doi: 10.1007/s12145-021-00571-z
[2] KHAN I, LEI H D, SHAH A A, et al. Climate change impact assessment, flood management, and mitigation strategies in Pakistan for sustainable future[J]. Environmental Science and Pollution Research, 2021, 28(23): 29720-29731. doi: 10.1007/s11356-021-12801-4
[3] LIU Z J, GUO S L, ZHANG H G, et al. Comparative study of three updating procedures for real-time flood forecasting[J]. Water Resources Management, 2016, 30(7): 2111-2126. doi: 10.1007/s11269-016-1275-0
[4] 王秀杰, 李丹丹, 苑希民, 等. 基于参数分级优化的水文气象耦合预报研究[J]. 天津大学学报(自然科学与工程技术版),2021,54(3):279-288 WANG Xiujie, LI Dandan, YUAN Ximin, et al. Coupled hydrometeorology forecasting based on hierarchical optimization of parameters[J]. Journal of Tianjin University (Science and Technology), 2021, 54(3): 279-288. (in Chinese)
[5] LI Z L, ZHANG X L, ZHU R, et al. Integrating data-to-data correlation into inverse distance weighting[J]. Computational Geosciences, 2020, 24(1): 203-216. doi: 10.1007/s10596-019-09913-9
[6] 熊立华, 刘烁楠, 熊斌, 等. 考虑植被和人类活动影响的水文模型参数时变特征分析[J]. 水科学进展,2018,29(5):625-635 XIONG Lihua, LIU Shuonan, XIONG Bin, et al. Impacts of vegetation and human activities on temporal variation of the parameters in a monthly water balance model[J]. Advances in Water Science, 2018, 29(5): 625-635. (in Chinese)
[7] DE MORAES CORDEIRO A L, BLANCO C J C. Assessment of satellite products for filling rainfall data gaps in the Amazon region[J]. Natural Resource Modeling, 2021, 34(2): e12298.
[8] 申睿. 山东省山丘区缺资料小流域暴雨洪水计算研究[D]. 济南: 山东大学, 2016. SHEN Rui. Research of storm and flood calculation in small ungauged basins at hilly areas of Shandong Province[D]. Jinan: Shandong University, 2016. (in Chinese)
[9] 陈华, 盛晟, 夏润亮, 等. 基于矩阵分解的降水时空插值方法[J]. 河海大学学报(自然科学版),2021,49(1):35-41 CHEN Hua, SHENG Sheng, XIA Runliang, et al. Spatiotemporal interpolation method of rainfall based on matrix decomposition[J]. Journal of Hohai University (Natural Sciences), 2021, 49(1): 35-41. (in Chinese)
[10] HUANG H P, LIANG Z M, LI B Q, et al. A new spatial precipitation interpolation method based on the information diffusion principle[J]. Stochastic Environmental Research and Risk Assessment, 2019, 33(3): 765-777. doi: 10.1007/s00477-019-01658-2
[11] RATA M, DOUAOUI A, LARID M, et al. Comparison of geostatistical interpolation methods to map annual rainfall in the Chéliff watershed, Algeria[J]. Theoretical and Applied Climatology, 2020, 141(3/4): 1009-1024.
[12] 吴孝情, 陈晓宏, 唐亦汉, 等. 珠江流域非平稳性降雨极值时空变化特征及其成因[J]. 水利学报,2015,46(9):1055-1063 WU Xiaoqing, CHEN Xiaohong, TANG Yihan, et al. Spatiotemporal variations and the causes of non-stationary extreme precipitation in the Pearl River Basin[J]. Journal of Hydraulic Engineering, 2015, 46(9): 1055-1063. (in Chinese)
[13] ENGLE R F, GRANGER C W J. Co-integration and error correction: representation, estimation, and testing[J]. Econometrica, 1987, 55(2): 251. doi: 10.2307/1913236
[14] 余威. 气象相似性网络构建及缺失气象要素数据的插补[D]. 重庆: 西南大学, 2015: 58. YU Wei. Construct meteorological similarity network and missing meteorological elements data interpolation[D]. Chongqing: Southwest University, 2015: 58. (in Chinese)
[15] 金倩芳. 无资料地区短期水文预报方法研究与应用[D]. 武汉: 华中科技大学, 2019. JIN Qianfang. Research and application on the short-term hydrological forecasting methods in the ungauged basins[D]. Wuhan: Huazhong University of Science and Technology, 2019. (in Chinese)
[16] ZIARH G F, SHAHID S, ISMAIL T B, et al. Correcting bias of satellite rainfall data using physical empirical model[J]. Atmospheric Research, 2021, 251: 105430. doi: 10.1016/j.atmosres.2020.105430
[17] SHARIFI E, SAGHAFIAN B, STEINACKER R. Downscaling satellite precipitation estimates with multiple linear regression, artificial neural networks, and spline interpolation techniques[J]. Journal of Geophysical Research: Atmospheres, 2019, 124(2): 789-805. doi: 10.1029/2018JD028795
[18] 彭安帮, 刘九夫, 马涛, 等. 辽宁省资料短缺地区中小河流洪水预报方法[J]. 水力发电学报,2020,39(8):79-89 doi: 10.11660/slfdxb.20200808 PENG Anbang, LIU Jiufu, MA Tao, et al. Flood forecasting method for medium-and small-size rivers short of hydrological data in Liaoning Province[J]. Journal of Hydroelectric Engineering, 2020, 39(8): 79-89. (in Chinese) doi: 10.11660/slfdxb.20200808
[19] 李琼, 陈红兵, 彭薇, 等. 基于降雨强度及降雨中心的瞬时单位线参数综合优化[J]. 三峡大学学报(自然科学版),2019,41(4):6-9, 15 LI Qiong, CHEN Hongbin, PENG Wei, et al. Comprehensive optimization of instantaneous unit hydrograph based on rainfall intensity and center changes[J]. Journal of China Three Gorges University (Natural Sciences), 2019, 41(4): 6-9, 15. (in Chinese)
[20] 覃武, 赵金彪, 黄荣成, 等. 台风“山竹”登陆结构变化及造成广西强降水异常分布的成因分析[J]. 热带气象学报,2019,35(5):587-595 QIN Wu, ZHAO Jinbiao, HUANG Rongcheng, et al. Cause analysis on the structural change of typhoon mangkhut during its landing and the abnormal distribution of heavy precipitation in Guangxi[J]. Journal of Tropical Meteorology, 2019, 35(5): 587-595. (in Chinese)
[21] LIU B Q, XU M, WANG J, et al. Evaluation of China’s marine economic growth quality based on set pair analysis[J]. Marine Policy, 2021, 126: 104405. doi: 10.1016/j.marpol.2021.104405
[22] ZHANG Q Y, XU P P, CHEN J, et al. Evaluation of groundwater quality using an integrated approach of set pair analysis and variable fuzzy improved model with binary semantic analysis: a case study in Jiaokou Irrigation District, east of Guanzhong Basin, China[J]. Science of the Total Environment, 2021, 767: 145247. doi: 10.1016/j.scitotenv.2021.145247
[23] LIU X P, XIA C F, CHEN Z W, et al. A new framework for rainfall downscaling based on EEMD and an improved fractal interpolation algorithm[J]. Stochastic Environmental Research and Risk Assessment, 2020, 34(8): 1147-1173. doi: 10.1007/s00477-020-01823-y
[24] 李秉晨, 于惠钧, 丁华轩, 等. 基于CEEMD和LSTM-ARIMA的短期风速预测[J]. 中国测试, 2022, 48(2): 163-168. LI Bingchen, YU Huijun, DING Huaxuan, et al. Short-term wind speed prediction based on CEEMD and LSTM-ARIMA[J]. China Measurement & Test, 2022, 48(2): 163-168. (in Chinese)
[25] ZHENG H M, DANG C L, GU S M, et al. A quantified self-adaptive filtering method: effective IMFs selection based on CEEMD[J]. Measurement Science and Technology, 2018, 29(8): 085701-1-085701-12. doi: 10.1088/1361-6501/aac990
[26] 黄旭升. 基于CEEMD信号处理技术的锚杆锚固质量无损检测方法研究[D]. 昆明: 昆明理工大学, 2019. HUANG Xusheng. Research on non-destructive testing method of bolt anchorage quality based on CEEMD signal processing technology[D]. Kunming: Kunming University of Science and Technology, 2019. (in Chinese)
[27] 任长秋. 农产品加工业FDI技术溢出时间效应及影响因素研究[D]. 重庆: 西南大学, 2020. REN Changqiu. The timing spillover effect of FDI and influencing factors in China’s agruicultrual product processing industry[D]. Chongqing: Southwest University, 2020. (in Chinese)
[28] 王亨力, 倪深海. 基于AHP-集对分析的矿井水资源利用风险评估[J]. 水利水运工程学报,2021(3):126-135 doi: 10.12170/0201120002 WANG Hengli, NI Shenhai. Risk assessment of mine water resource utilization based on analytic hierarchy process and set pair analysis[J]. Hydro-Science and Engineering, 2021(3): 126-135. (in Chinese) doi: 10.12170/0201120002
[29] 李小朦. 基于CEEMD和LRSD-TNNSR的柔性薄壁轴承故障特征提取[D]. 广州: 华南理工大学, 2020. LI Xiaomeng. Fault feature extraction of flexible thin-walled bearings based on CEEMD and LRSD-TNNSR[D]. Guangzhou: South China University of Technology, 2020. (in Chinese)
[30] ZHANG Y A, YAN B B, AASMA M. A novel deep learning framework: prediction and analysis of financial time series using CEEMD and LSTM[J]. Expert Systems With Applications, 2020, 159: 113609. doi: 10.1016/j.eswa.2020.113609
[31] AUERSWALD K, HAIDER J. Runoff curve numbers for small grain under German cropping conditions[J]. Journal of Environmental Management, 1996, 47(3): 223-228. doi: 10.1006/jema.1996.0048
[32] AL-GHOBARI H, DEWIDAR A Z. Integrating GIS-based MCDA techniques and the SCS-CN method for identifying potential zones for rainwater harvesting in a semi-arid area[J]. Water, 2021, 13(5): 704. doi: 10.3390/w13050704
[33] 徐赞, 吴磊, 吴永祥, 等. SCS-CN模型改进及其径流预测[J]. 水利水运工程学报,2018(3):32-39 XU Zan, WU Lei, WU Yongxiang, et al. Improvement and runoff prediction of SCS-CN model[J]. Hydro-Science and Engineering, 2018(3): 32-39. (in Chinese)
[34] 蒙海波. 广西中南部玉林地区传统围合式建筑的天井空间微气候调节效果研究[D]. 南宁: 广西大学, 2020. MENG Haibo. Study on the effect of microclimate regulation on traditional enclosed buildings in Yulin area of south-central Guangxi[D]. Nanning: Guangxi University, 2020. (in Chinese)



 Email Alerts
Email Alerts RSS
RSS
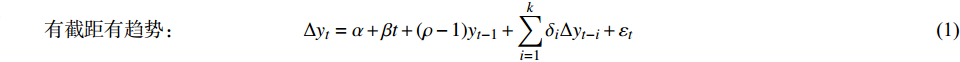
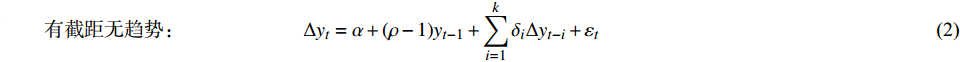
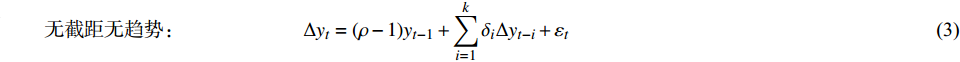
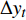

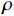
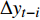
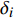
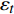


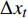
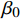
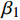

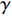
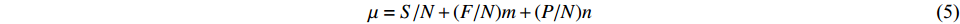
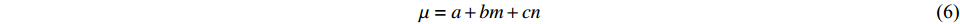
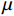

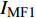
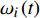
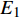

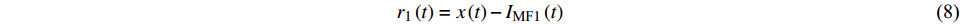
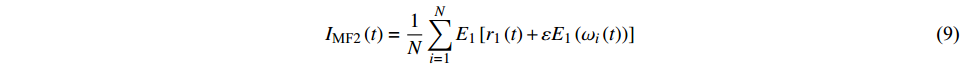
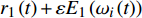
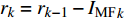
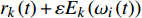
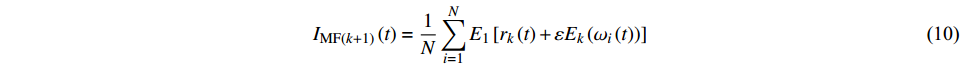
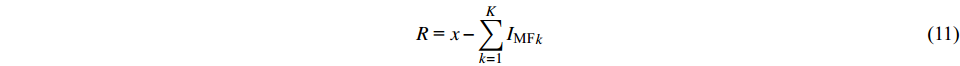
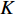
 下载:
下载: