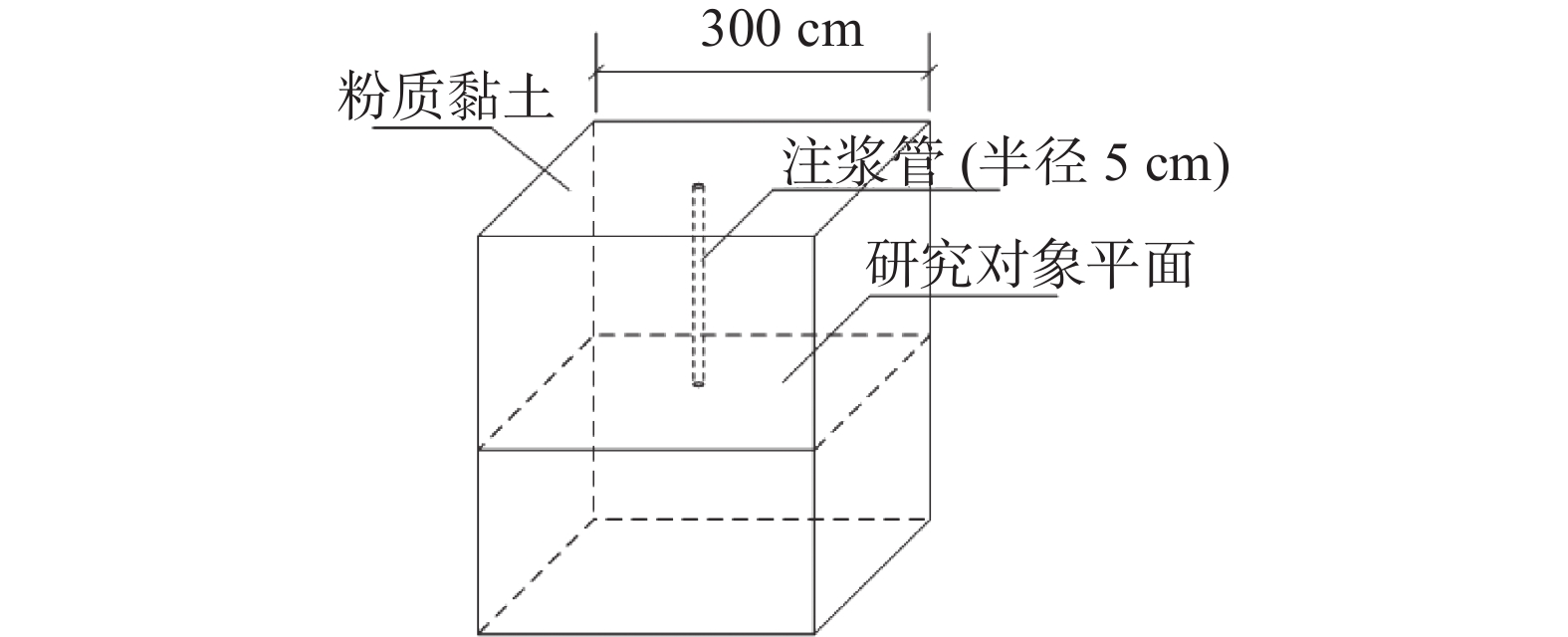
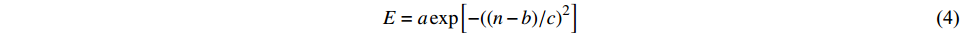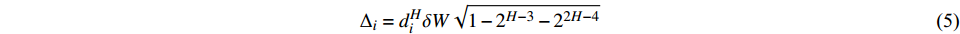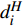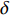Numerical simulation of split grouting of heterogeneous clay with different permeability coefficient
-
摘要: 针对地下工程中软弱黏土地层病害治理问题,考虑黏土材料的非均质性与低渗透性,对黏土进行劈裂注浆加固特性分析。基于Weibull分布函数理论构建非均质黏土地层模型,对黏土进行劈裂注浆加固模拟;基于注浆模拟计算结果,分析不同均质度与渗透系数对黏土劈裂注浆效果的影响。结果表明:土体劈裂注浆难度随均质度的增大而增加,均质度较高土体劈裂后产生的裂缝较为单一,裂缝分布范围较小;均质度较低土体劈裂产生的裂缝宽度较大,裂缝影响范围更广。浆脉扩展的长度及增长幅度随土体渗透系数的增大而减小,高渗透系数土体的劈裂浆脉宽度要大于低渗透系数的土体,渗透系数较小土体的浆脉长度始终比较大,浆脉距注浆孔越远,其宽度越小。研究可为软弱黏土地层劈裂注浆的工程应用提供指导。Abstract: Considering the heterogeneity and low permeability of the clay materials, the fracture grouting reinforcement characteristics of the clay are analyzed in view of the disease treatment of soft clay stratum in underground engineering. Based on Weibull distribution function theory, a heterogeneous clay formation model was constructed, and the clay was simulated by splitting grouting. Based on the results of grouting simulation, the influence of different uniformity and permeability coefficients on the grouting effect of clay splitting was analyzed. The results show that the difficulty of splitting grouting increases with the increase of the uniformity of soil mass, and the crack produced by splitting of soil mass with higher uniformity is relatively single and the distribution range of crack is smaller. The crack width is larger and the influence range is wider when the soil is less homogeneous. The length and growth amplitude of slurry vein expansion decrease with the increase of soil permeability coefficient. The width of slurry vein in the soil with a large permeability coefficient is larger than that in the soil with a low permeability coefficient. The length of slurry vein in the soil with a small permeability coefficient is always larger, and the farther the slurry vein is from the grouting hole, the smaller the width. The research has important guiding significance for the engineering application of fracture grouting in soft clay stratum.
-
在地铁、矿山、隧道和综合管廊等地下工程施工过程中,常会遇到软弱黏土地层[1-3],软黏土具备高压缩性、低渗透性、低强度等特性,对软弱黏土地层处理不当,会造成地层的不均匀沉降,甚至会引起灾害性涌水[4-5]。实际工程中常采用劈裂注浆手段对软黏土地层进行加固。虽然劈裂注浆工艺很成熟,但是相关物理试验的可重复性较差[6],劈裂注浆扩散过程可视化程度较低,而数值模拟技术具备经济、合理、形成结果可视化程度高等优势,是目前国内外开展黏土劈裂注浆研究的重要手段。
土具有原位变异性与非均质性,土体物理力学特征及空间分布呈非均匀性[7-8]。Weibull分布、对数正态分布、极值I型分布是研究材料非均质性问题的常用建模方法,其中Weibull分布在材料的性质描述上应用较广[9-11]。黏土材料的非均质性主要表现为孔隙率、弹性模量等物理力学参数在空间上的差异[12-13]。黏土物性参数的空间非均质性会影响劈裂注浆的效果。考虑软弱黏土层物性参数的空间非均质性,利用Weibull分布函数理论构建非均质黏土地层模型,是分析劈裂注浆加固软弱黏土效果的重要方法。
黏土地层渗透系数是影响劈裂注浆效果的重要因素,渗透系数对浆液扩散形态影响十分明显[14-15]。本文运用Weibull分布函数理论构建非均质黏土地层模型,开展劈裂注浆加固黏土地层的数值模拟,研究劈裂注浆过程中浆液压力及土体主应力分布的特征,从均质度与渗透系数两方面进行劈裂注浆加固黏土的效果分析。
1. 非均质黏土地层模型构建
1.1 Weibull分布函数理论模型
在Weibull分布条件下,材料各参数之间的关系可由式(1)[7]建立:
$$ f\left( x \right) = \frac{m}{\alpha } {\left( {\frac{x}{\alpha }} \right)^{m - 1}}{{\rm{exp}}[{ - {{( {x/\alpha } )}^m}}]} $$ (1) 式中:x为土体材料细观单元体的力学性质参数;α为Weibull分布函数的尺度参数;m为Weibull分布函数的形状参数。其中,形状参数m也即材料均质度,概率密度函数的峰值和分布范围主要与m值的大小有关,m值越小,函数峰值也就越小,分布范围越广,参数分布越离散,代表土体均匀性越差。尺度参数则主要控制分布均值,数值上接近分布参数的均值。
对式(1)进行积分得:
$$ F\left( x \right) = \int_\alpha ^x {f\left( x \right){\rm d}x = } \int_\alpha ^x {\frac{m}{\alpha }} {\left( {\frac{x}{\alpha }} \right)^{m - 1}}{{\rm{exp}}[{ - {{( {x/\alpha } )}^m}}]}{\rm d}x $$ (2) 最后得概率分布函数为:
$$ F\left( x \right) = 1 - \exp \left[ { - {{\left( {\frac{x}{\alpha }} \right)}^m}} \right]$$ (3) 1.2 孔隙率对Weibull分布的建模验证
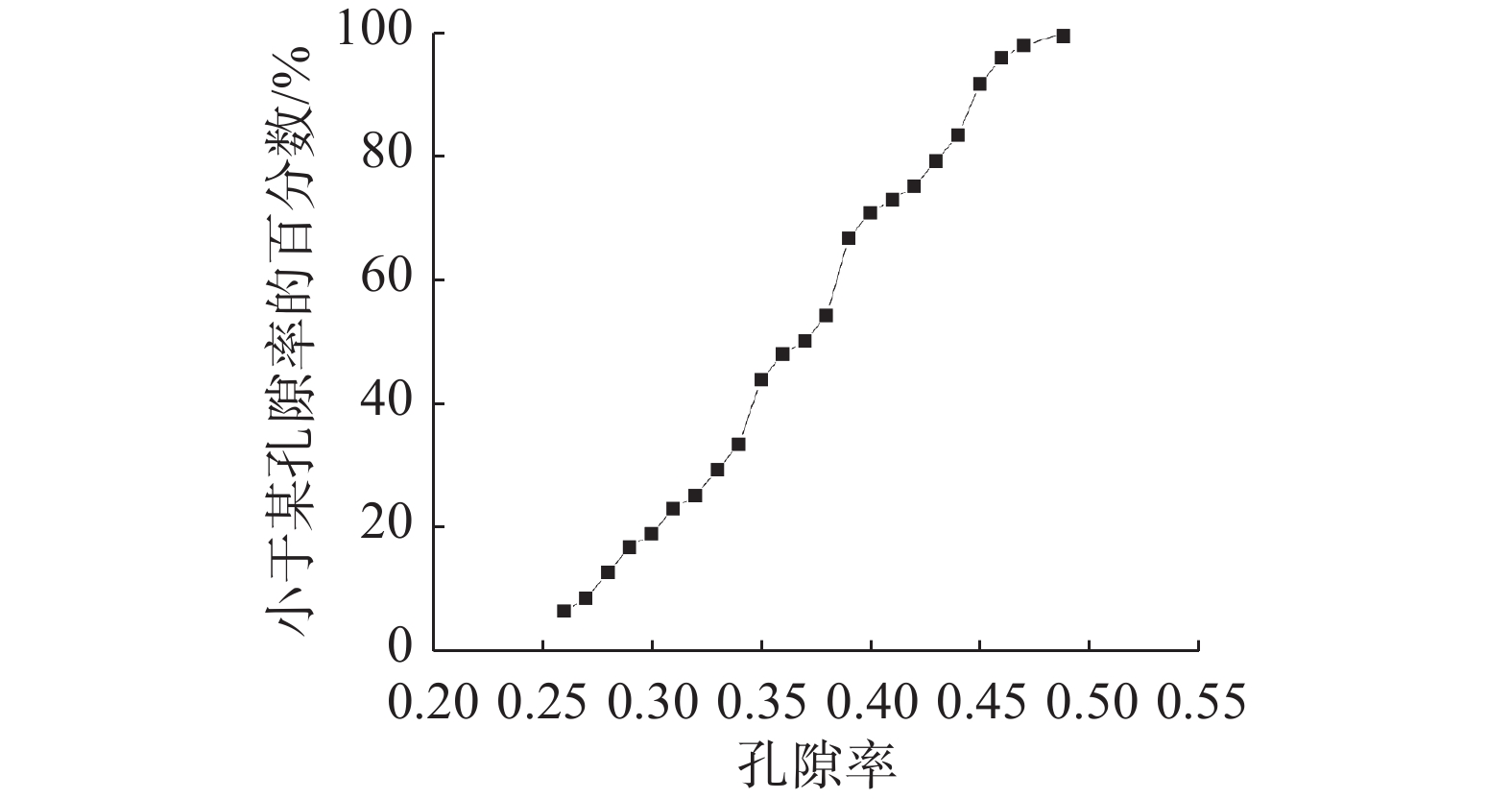
考虑黏土材料的非均质性,利用宜昌市某地下工程黏土层的孔隙率勘察资料进行Weibull分布的建模验证。现场有TK1、TK2、TK3、TK4、TK5、TK6共6个取土孔点和60个勘探点,孔隙率勘探结果如表1所示。为降低现场勘察过程中的误差影响,对勘探结果进行优化,去掉各取土孔点的10个勘探结果中的最大值与最小值,绘制孔隙率勘探结果概率见图1。
表 1 现场孔隙率勘探值Table 1. Field porosity exploration valueTK1 TK2 TK3 TK4 TK5 TK6 勘探深度/m 孔隙率 勘探深度/m 孔隙率 勘探深度/m 孔隙率 勘探深度/m 孔隙率 勘探深度/m 孔隙率 勘探深度/m 孔隙率 0 0.45 0 0.44 0 0.46 0 0.50 0 0.40 0 0.46 1.20 0.26 0.55 0.41 0.40 0.48 1.11 0.49 0.96 0.36 0.46 0.26 1.53 0.28 1.57 0.39 1.21 0.31 1.56 0.38 1.58 0.44 2.29 0.39 3.19 0.26 1.75 0.28 2.66 0.40 1.98 0.25 2.68 0.33 2.29 0.36 3.81 0.45 3.18 0.25 3.30 0.43 2.89 0.35 3.11 0.42 2.93 0.25 4.80 0.38 3.61 0.27 3.61 0.30 3.21 0.35 3.26 0.25 3.06 0.33 5.35 0.49 4.25 0.35 3.92 0.35 3.84 0.37 4.88 0.29 3.72 0.44 5.71 0.47 5.28 0.39 4.09 0.43 4.91 0.29 5.19 0.34 3.84 0.48 6.24 0.39 6.30 0.48 4.30 0.27 5.98 0.45 5.78 0.35 4.36 0.31 6.53 0.26 6.35 0.34 5.28 0.45 6.63 0.39 6.58 0.32 5.66 0.39 将孔隙率的勘测数据点绘于线性化处理后的Weibull坐标下,采用最小二乘法进行线性拟合,拟合结果表明Weibull分布相关系数R2为0.990 4,说明拟合效果较好。由此可知,使用Weibull分布函数可较好描述黏土地层参数的非均质性。
1.3 土层物性参数相关性数学模型
孔隙率是土体变形的内因和决定土体物理力学性质的主要因素,是影响多孔介质内流体传输性能的重要参数。孔隙率与弹性模量等土体物性参数之间存在着一定的函数相关性[14]。有研究[12-14]认为,孔隙率与弹性模量之间可由如下函数表述:
$$ E = a\exp \left[ { -((n-b)/c)}^2 \right] $$ (4) 式中:a、b、c均为常数,a=45.50、b=0.056 78、c=0.365 4。
1.4 基于Weibull分布的非均质黏土地层构建
考虑土性参数的相关性,利用Weibull分布函数模型及随机分形插值算法,结合工程勘察资料,建立不同均质度条件下的非均质黏土地层模型。基本步骤如下:(1)对地层已知孔隙率进行统计分布;(2)结合随机分形插值算法,利用Weilbull分布模拟实际地层空间的孔隙率非均质分布;(3)根据不同均质度条件(Weilbull分布形状参数),构造以孔隙率为基本量,弹性模量为变化量的非均质地层模型。
以分形布朗运动为基础的随机分形理论常用来描述许多地质现象,如地层参数、测井数据的自相似性,而随机分形插值算法可用来模拟实际地层空间孔隙率的非均质分布[12]。在随机分形插值算法中,为了保证布朗运动中的自相似性,每次计算新的单元数据时都须附加随机位移量Δi。通过对研究区域内的孔隙率进行统计分析得到分形维数取值D为1.023,由赫斯特指数与分形维数的关系H=2−D,得到赫斯特指数H=0.977。
由文献[13]可得满足Weibull分布的随机位移量Δi计算式为:
$$ {\Delta _i} = d_i^H \delta W\sqrt {1 - {2^{H - 3}} - {2^{2H - 4}}} $$ (5) 式中:
$ d_i^H $ 为分形计算中细分后的线段间距;H为赫斯特指数;i为单元数据编号;$ \delta $ 为地层参数的特征值;W为服从Weibull分布的随机数。根据Weibull分布函数特征,利用现场孔隙率地勘资料,尺度参数取为1。结合随机分形插值算法,模拟实际地层的孔隙率分布见图2。
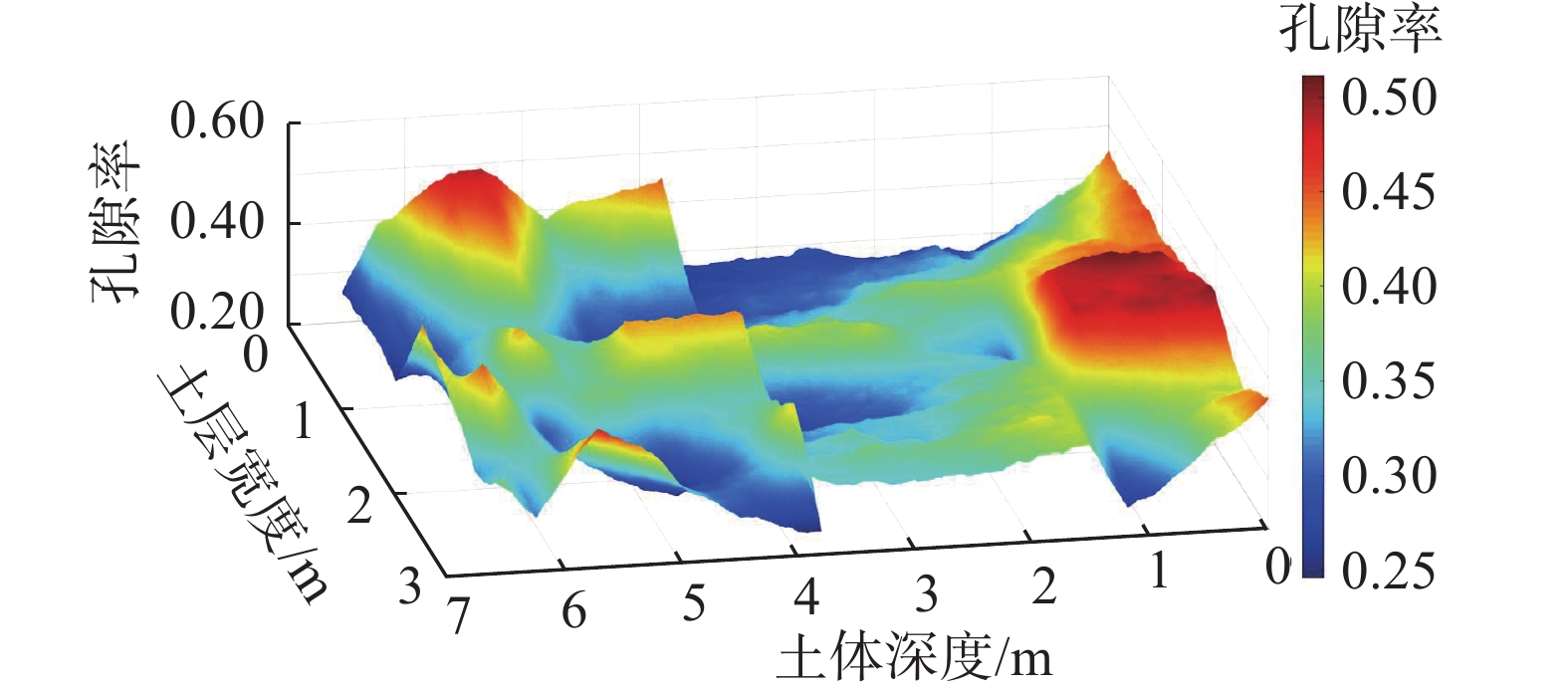
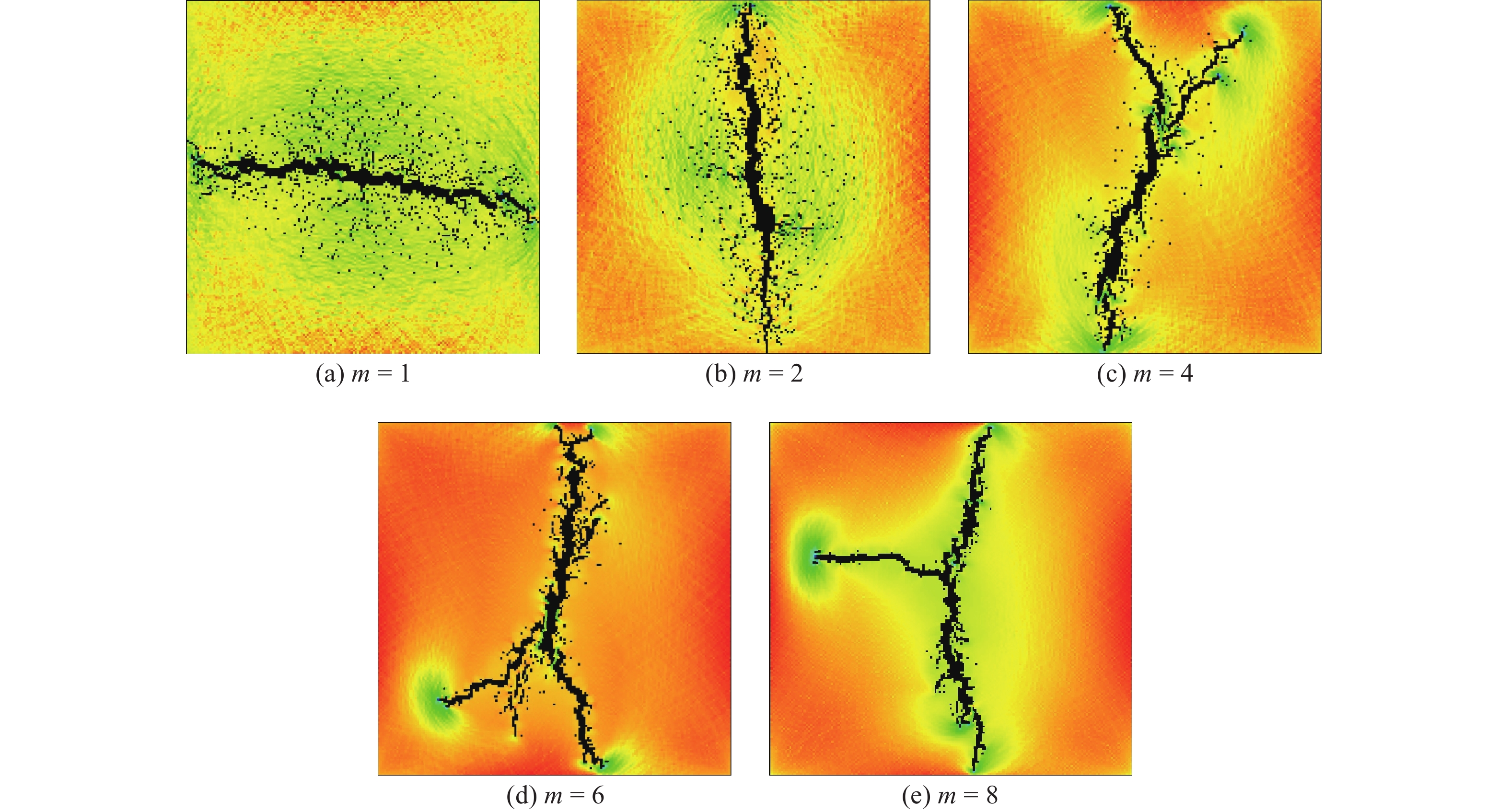
结合孔隙率与弹性模量的函数相关性,选取均质度分别为1、2、4、6、8的土体构建二维非均质黏土地层,研究平面土体边长为3 m,可构造不同均质度条件下的土体弹性模量分布(图3)。
由图3可知,均质度不同,土体的弹性模量也不相同,其中颜色差异性随着均质度的提高而减小,也即材料越均匀。
2. 基于非均质地层模型的劈裂注浆模拟
数值模拟计算时,材料模型假设[16]如下:(1)注浆过程中,浆液流型始终不变,且为不可压缩、受力相同的牛顿流体,被注土体在水压下的损伤计算符合摩尔库伦准则;(2)劈裂通道侧壁光滑,即注浆浆液在通道侧壁处的流动速度为0,模型计算边界的位移为0;(3)浆液的组分不会随着注浆过程而改变,忽略渗滤效应;(4)浆液在土体中的流动符合Biot流固耦合模型。
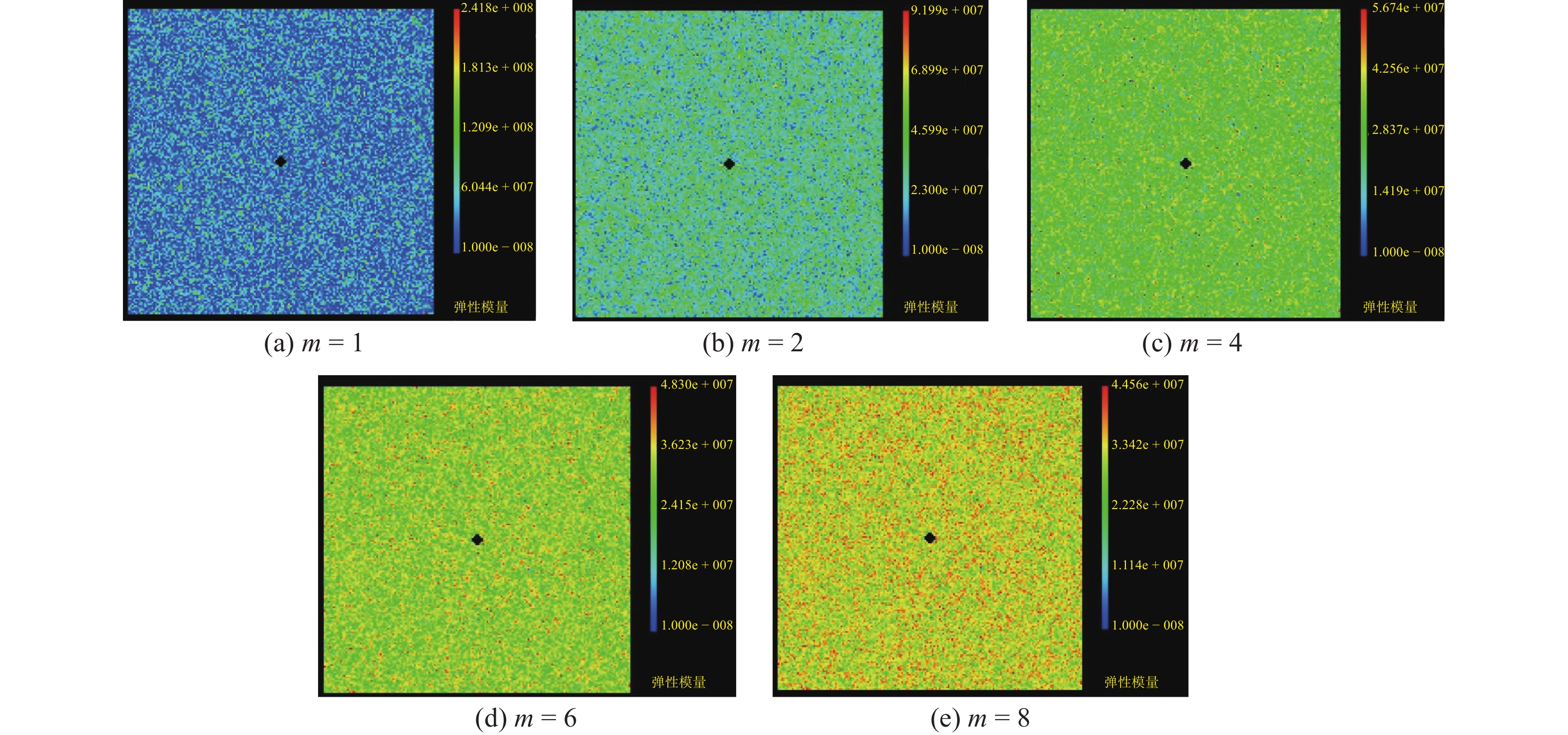
为了真实反映土体在水平面发生劈裂时的劈裂效果,取注浆管位于土体中心,端部为注浆孔的方形土体(高度为300 cm)作为劈裂注浆几何立面模型。如图4所示,研究对象取自劈裂注浆几何立面模型中所截取的一个平面,该平面土体边长为300 cm,注浆孔半径为5 cm,共生成170×170=28 900个单元。为了节省模拟时间,设置模型中的注浆孔初始有效压力为0,同时以每步0.01 MPa的速率增加,直至土体劈裂注浆的裂纹扩展最终导致土体宏观失稳破坏。在土体边界的位移和水压均设为0,采用应力加载方式及Biot耦合方程,耦合系数为0.1,破坏条件选取Mohr-Coulomb准则。
基于现场资料及文献研究[17-19],确定土体相关力学参数如表2所示。
表 2 土体物理指标参数Table 2. Physical index parameters of soil力学参数 参数值 力学参数 参数值 均质度 1, 2, 4, 6, 8 泊松比 0.35 弹性模量/Pa 由地层不同孔隙率
参数值确定孔隙水压力系数 0.5 黏聚力/MPa 0.02 细观抗压强度/MPa 0.5 内摩擦角/° 22 初始有效压力/MPa 0 渗透系数/(m·d−1) 0.50, 0.05 单步增量/MPa 0.01 2.1 土体劈裂过程中浆液压力的分布变化
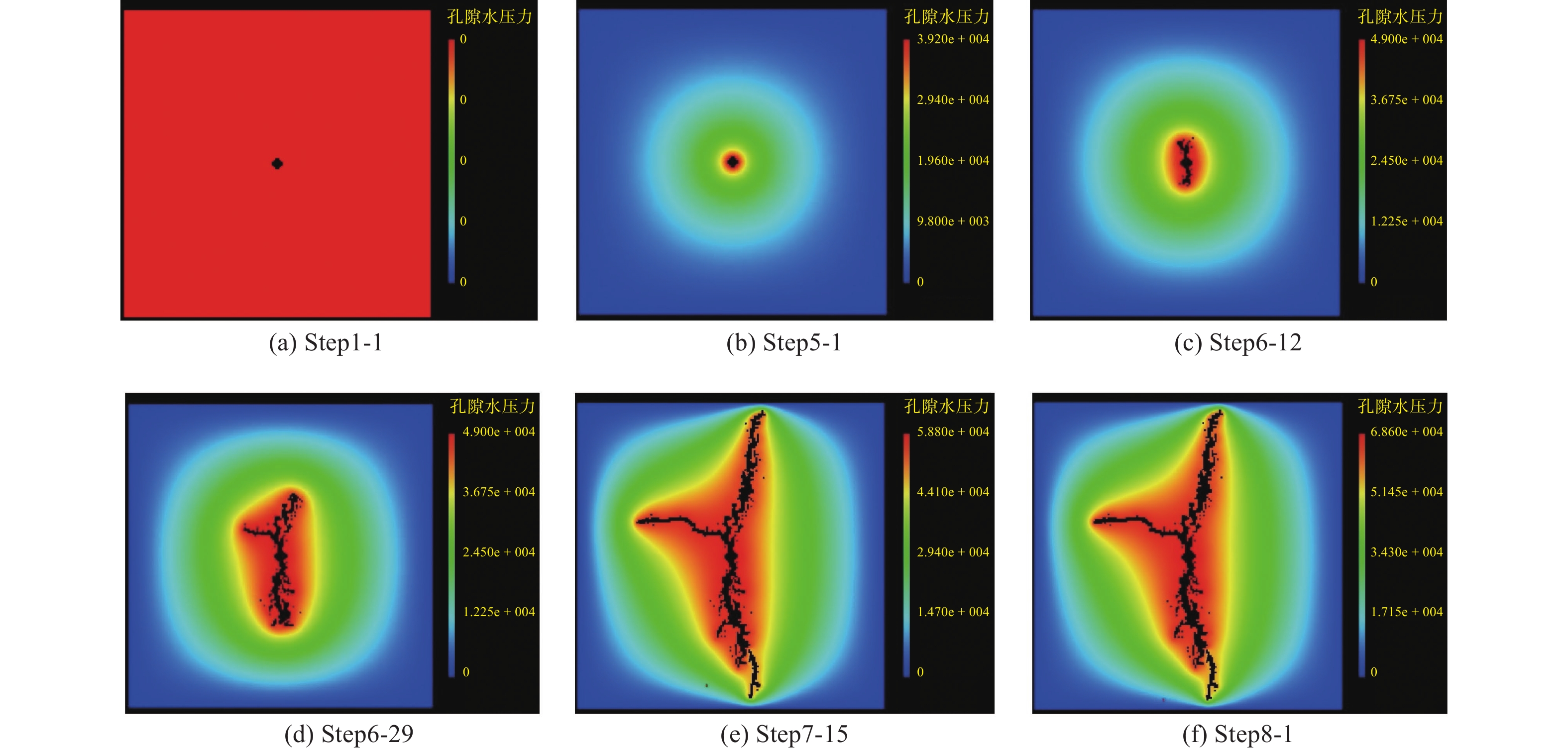
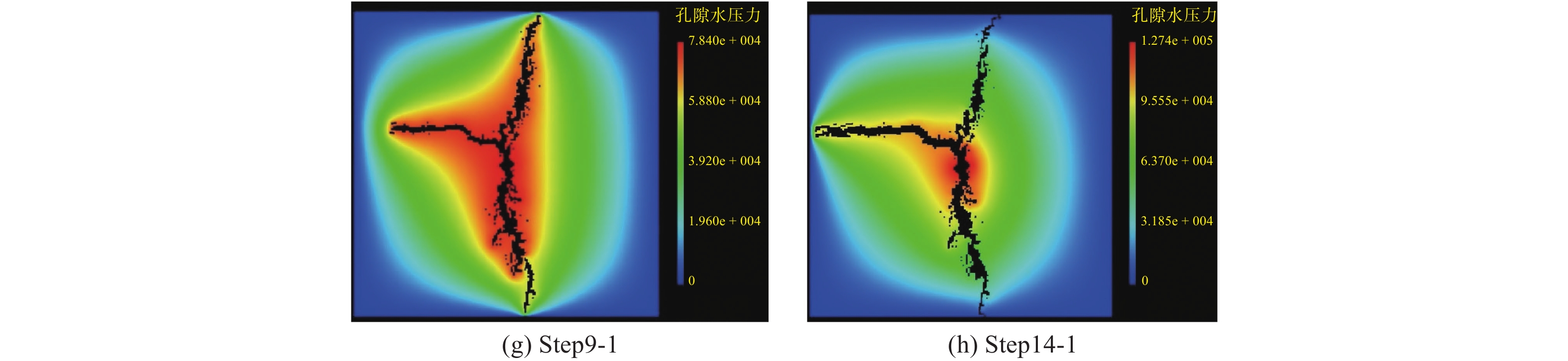
非均质黏土劈裂注浆过程的浆液压力分布变化如图5所示。
由图5可知,随着注浆过程的推进,注浆压力不断提升,浆液压力逐渐向土体边缘扩散。在注浆初始阶段,浆液压力主要以注浆孔呈现中心对称的分布,并且在注浆孔处的浆液压力最大,向四周不断衰减,同时形成浆液压力环。随着注浆压力的提升,注浆孔附近的单元开始出现损坏的现象,浆液压力等压环呈现不规则的变化,见Step6-12,在注浆孔附近的高压区域显得尤为明显。裂缝处浆液压力等压环向外不断扩散,在裂缝附近的浆液压力比土体的其他区域要大,这说明裂缝的形成有利于浆液压力的扩散,见Step6-29~Step7-15。随着注浆过程的继续推进,裂缝不断扩展至土体边缘,此时,浆液压力分布比较规则,存在裂缝的地方浆液压力较高,见Step8-1、Step9-1。若注浆压力继续提升,土体将开始出现损坏,此时,等压环再次不规则,只有注浆孔附近的浆液压力较大,裂缝附近的浆液压力开始递减,见Step14-1。
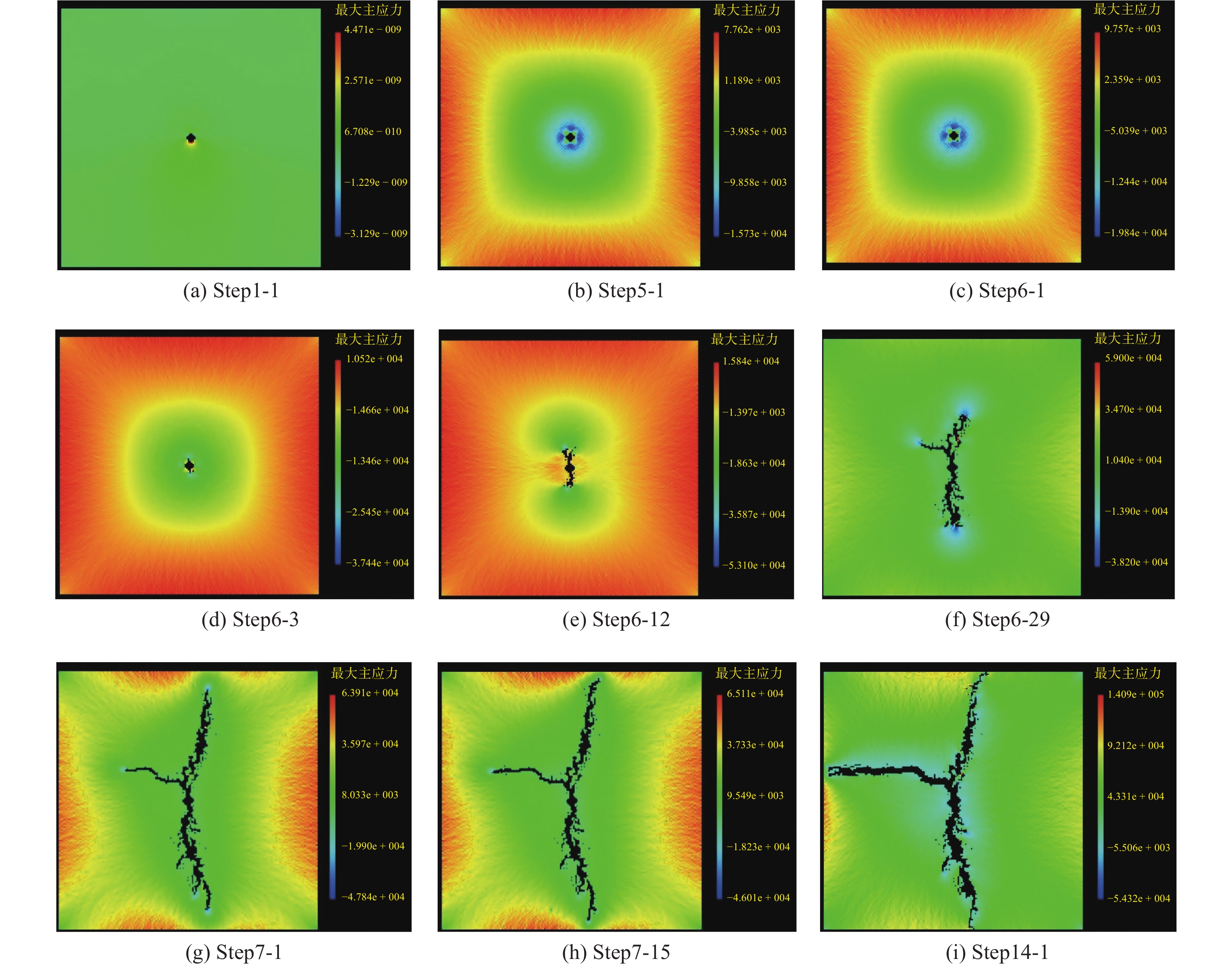
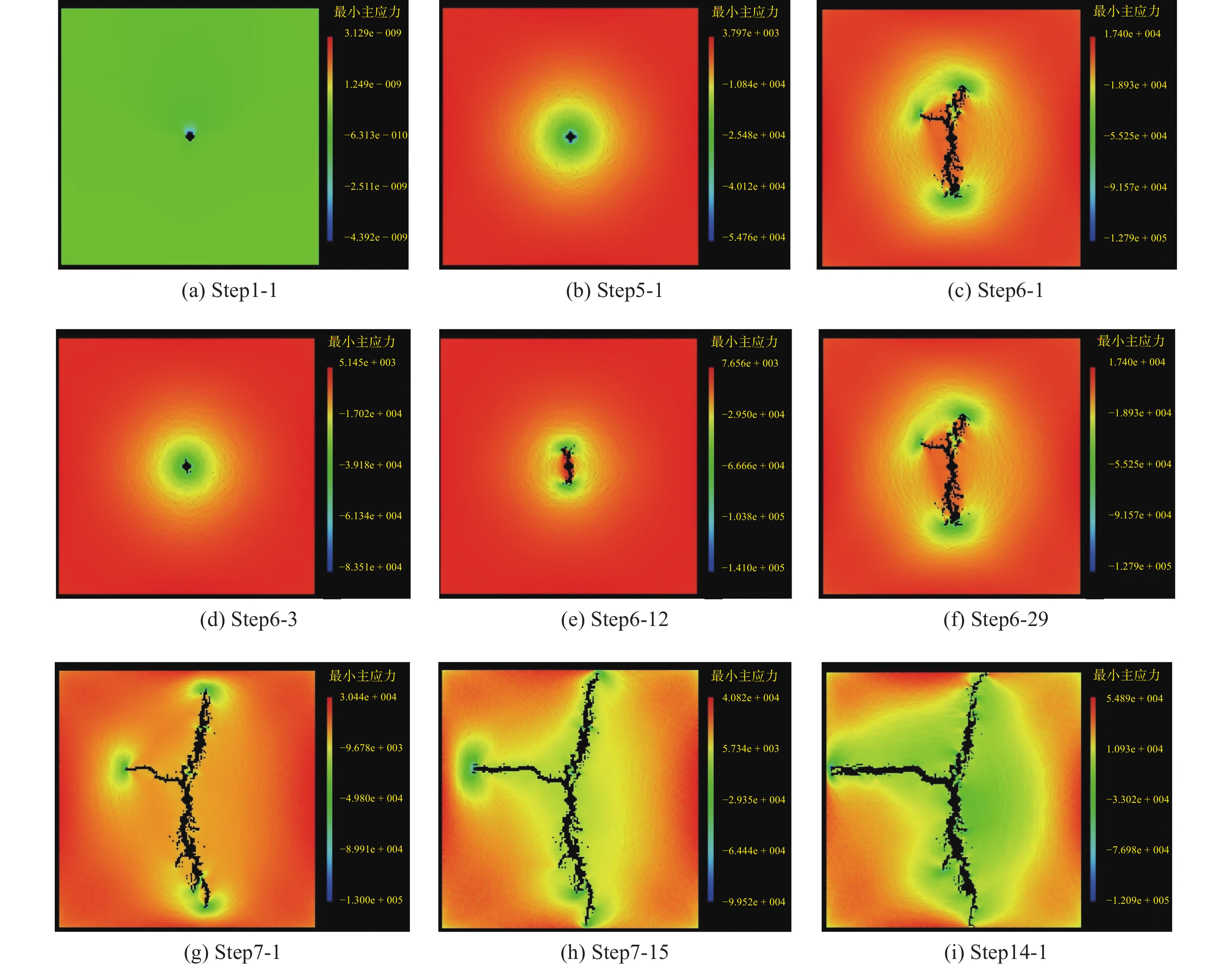
2.2 土体劈裂过程中主应力的变化
非均质黏土劈裂注浆过程的最大及最小应力分布分别见图6和图7。由图6与7可知,最大主应力与最小主应力的影响范围总体上随着注浆压力的提高而不断扩大。在Step1-1~Step5-1过程中,注浆压力比较低,最大主应力与最小主应力分布于注浆孔附近的有限范围内,还未向外延伸,并出现应力圈的情况;在Step6-1时,注浆孔周围的少量单元发生破坏现象,随着注浆的推进、注浆压力的提升,注浆孔周围单元破坏面积增大,此时损坏单元顶端的最大主应力与最小主应力较小,随着有效注浆压力的继续增大,破坏单元顶端开始出现裂缝,见Step6-3;当注浆压力继续提升时,裂缝开始延伸,最大主应力与最小主应力的影响范围开始增大,此时,裂缝顶端的最大主应力最小,在裂缝两侧及注浆孔附近较大,在土体没有被裂缝波及的区域应力依然比较大,同时在两个裂缝顶端形成两个应力滞回圈,见Step6-12;随着注浆压力进一步提升,裂缝开始向土体的边缘发展,此时,裂缝顶端的最大主应力与最小主应力最小,土体边缘的应力较大,其他区域应力较小,同时产生了新的裂缝,见Step6-29;之后裂缝长度不断增大,土体的最大主应力与最小主应力出现反弹现象,当注浆压力继续提升时,裂缝宽度开始加大,如Step7-1所示,此时裂缝长度基本不变。随着注浆压力的提升,裂缝向试件边缘发展,裂缝两侧的最大主应力与最小主应力逐渐减小,见Step7-15~Step14-1。如注浆压力继续提升,土体开始出现破坏现象,直至土体发生失稳。
对图5~7所呈现的T形裂缝状态进行分析。劈裂注浆裂缝扩展的步进方式受注浆压力影响较大,同时劈裂注浆裂缝状态可以引导浆液压力的分布状态。注浆初期,当注浆压力较小时,土体未能启裂;随着注浆压力的增大,当浆液压力大于土体最小主应力时,土体开始启裂,之后浆液进入裂缝;随着浆液的不断注入,裂缝中压力不断增加,裂缝继续扩展,浆液压力也随之作用于新的裂缝面;待浆液扩展到一定距离,浆液压力不足以继续劈裂前方土体时,裂缝停止扩展,此时或将会在注浆孔附近出现1~2条新的裂缝;随着注浆进程的推进,新裂缝基于同样的劈裂注浆机理进行变形发展。在注浆后期,裂缝后端的土体即注浆孔附近的土体会被浆液加固,使得注浆孔附近的土体不易出现新的劈裂通道,这可能是土体最终呈现T形裂缝的重要原因。
3. 均质度对非均质黏土劈裂注浆效果的影响
3.1 裂缝状态分布
不同均质度土体试样的劈裂注浆效果见图8。由图8可知,均质度对浆脉分布的影响很大,可以总结为:当均质度较低时,土体容易被浆液劈裂,形成的裂缝数量比较多,浆液扩散范围较广,裂缝的宽度较大,主裂缝较单一;均质度较高时,土体较难被浆液劈裂,形成的裂缝数目较少,裂缝分布较为集中,而且主裂缝较多。土体劈裂注浆时,裂缝基本上产生于土体较为薄弱的位置。从裂缝的发展可以看出土体劈裂注浆的机理:加固土体方式主要是通过注浆过程中浆脉对土体的挤压作用及浆液和土体形成的结石体;当土体均质度较低时,劈裂时产生的裂缝单一,主要通过浆液对裂缝的填充并形成结石体来提高土体强度;当土体均质度较高时,劈裂时形成网状裂缝,此时通过浆液运移过程中对土体产生的挤压作用及空间骨架作用来提高土体强度。
3.2 浆液压力分布
不同均质度土体劈裂注浆的浆液压力分布如图9所示。由图9可知,在注浆孔附近的浆液压力最大,向外递减,土体边缘的浆液压力最小,并且形成等压环。由于浆液压力的分布是由裂缝发展决定的,所以均质度不同时浆液压力的分布也就不同。当均质度较低时,浆液等压环的面积大致相等,如图9中m=1及m=2时所示。随着均质度的增大,由于主裂缝增加,此时最大浆液压力分布在试件的中心区域,分布范围要比均质度低时的更广,但是高压等压环和低压等压环的宽度有所差别,低压分布的范围更广泛,高压环的宽度小于低压环。
4. 渗透系数对非均质黏土劈裂注浆效果的影响分析
4.1 渗透系数对浆脉长度的影响
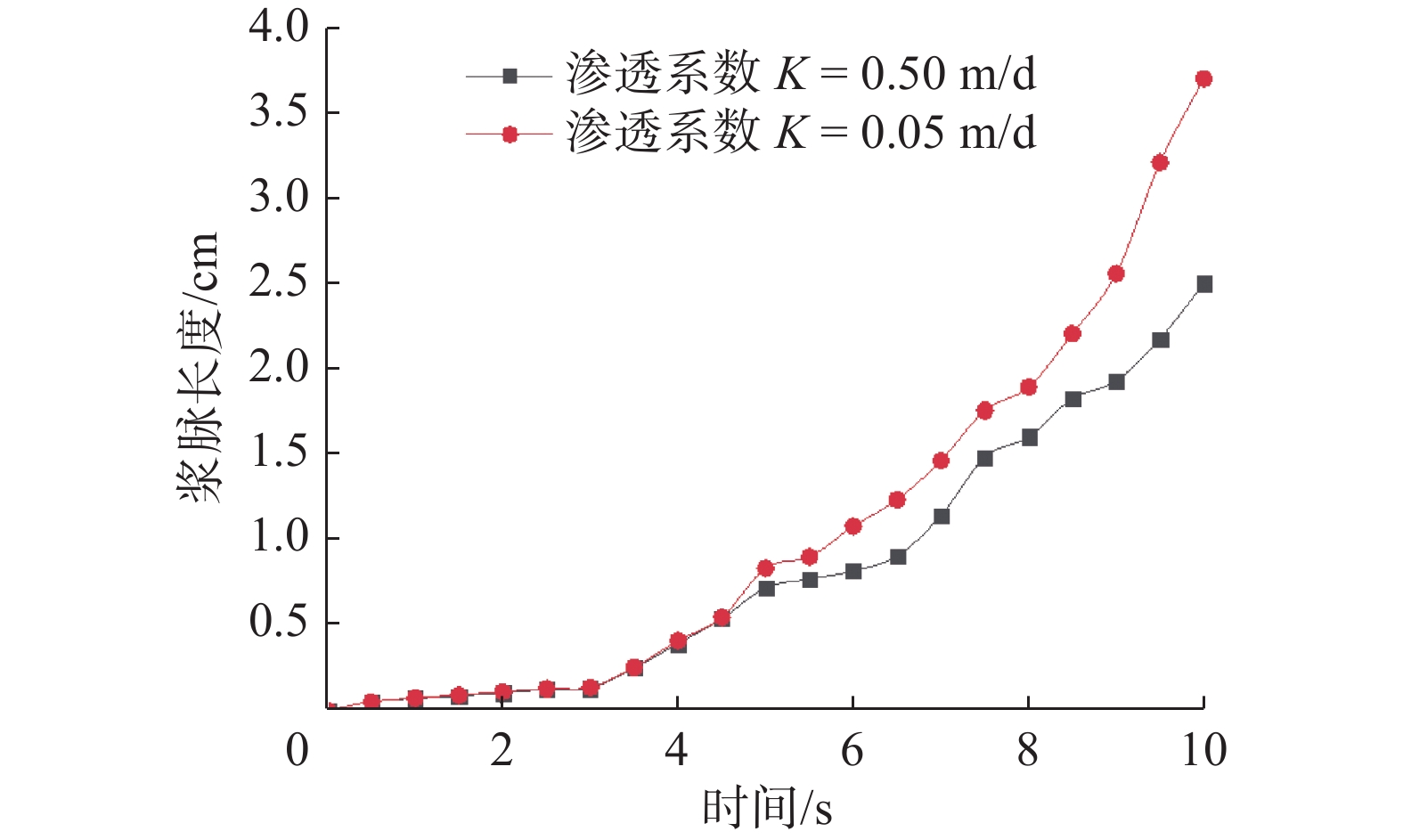
在均质度都为8的条件下,当渗透系数K分别为0.05和0.50 m/d时,浆脉长度随注浆时间变化关系见图10。
由图10可知,刚开始注浆时,渗透系数对浆脉长度的影响不大,随着注浆时间的延长,渗透系数开始发挥作用,在第5 s时,浆脉的长度差异开始明显,渗透系数大的土体浆脉扩展的长度比渗透系数小的土体的小,同时渗透系数较大土体的浆脉长度增长幅度较低,渗透系数较小土体的浆脉长度在第9 s时增幅很大。这是因为在注浆过程中,渗透系数较小的土体更难劈裂,但是一旦产生裂缝,其增长速率特别快;而渗透系数较大的土体劈裂形式更像渗透注浆,其裂缝的增长速度较慢。
4.2 渗透系数对浆脉宽度的影响
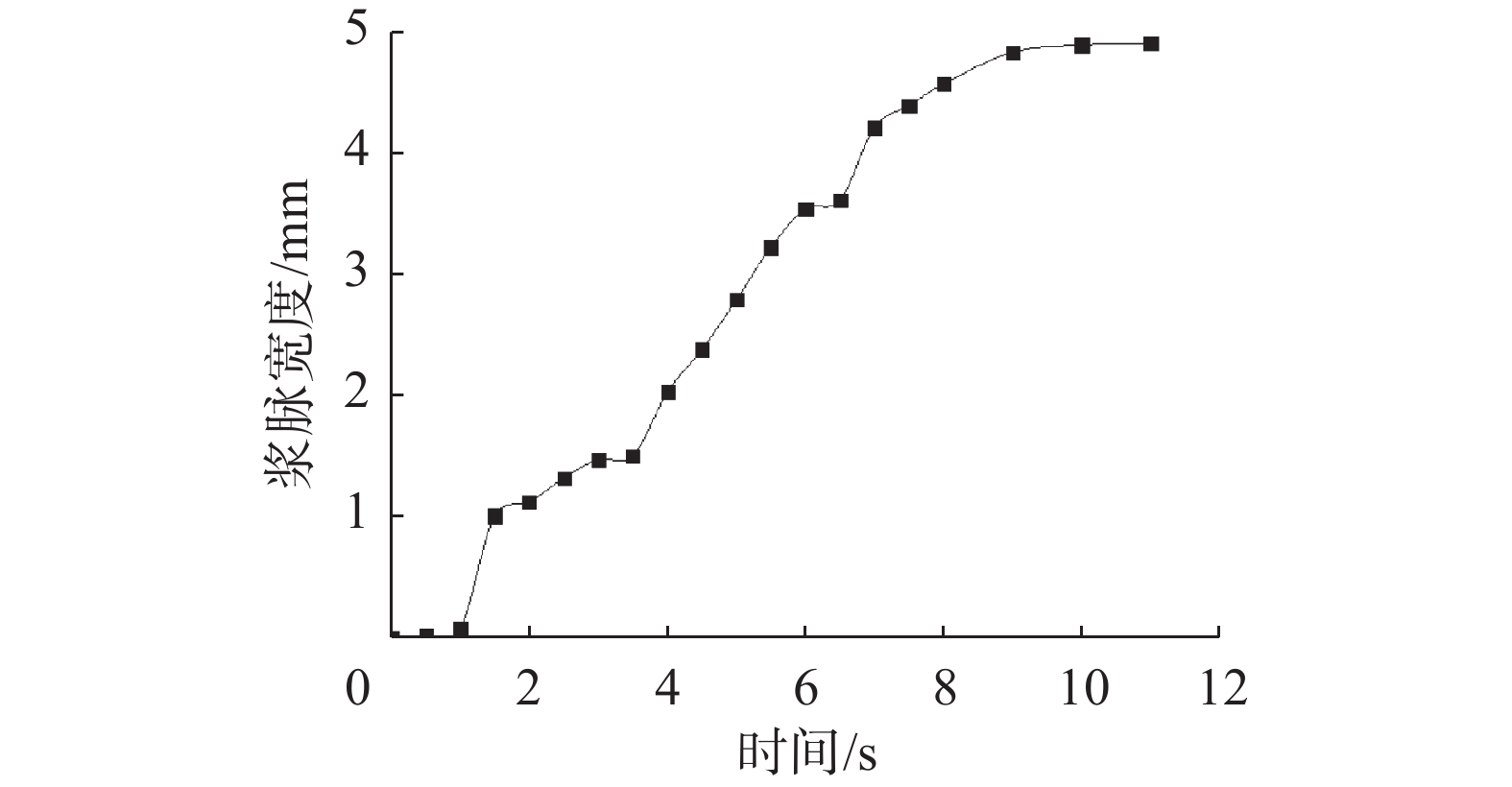
在均质度都为8的条件下,当渗透系数分别为0.05和0.50 m/d时,浆脉宽度随注浆时间变化关系如图11所示。距离注浆孔100 cm处不同时刻监测的浆脉宽度变化如图12所示。
由图11可知,渗透系数对浆脉宽度的影响贯穿整个注浆过程,当土体发生劈裂后,渗透系数较小的土体,产生的裂缝宽度要远大于高渗透系数的土体。这是因为渗透系数较小的土体难以劈裂,一旦发生劈裂,其裂缝的发展速度很快,会迅速向四周扩展。从图11还可以发现,距离注浆孔的距离越远,其产生的劈裂浆脉宽度越小。由浆液压力分布变化分析可知,这是因为在注浆孔附近的浆液压力最大,浆液压力圈向外呈现不断衰减的趋势,也就是说在注浆孔附近产生的劈裂浆脉宽度最大,在土样的边缘部位浆液压力最小,产生的劈裂浆脉宽度最小。
从图12可以发现,劈裂裂缝刚开始的宽度极小,随着注浆时间的推移,宽度逐渐增大,并趋于稳定。在注浆开始阶段,裂缝长度的增长速度要快于宽度;当浆液压力降低时,裂缝两侧的土体得以挤密,此时裂缝的宽度开始增加;到注浆后期,土体产生的裂缝已经被浆液填充,形成浆-土混合体,没有多余的孔隙,浆脉宽度不再迅速增长,而是趋于平稳。
5. 结 语
(1)针对地下工程中软弱黏土地层病害治理问题,考虑黏土材料的非均质性,基于Weibull分布函数理论,利用实际工程中黏土地层的孔隙率地勘资料,构建二维非均质黏土地层模型,可以很好地模拟劈裂注浆加固黏土效果。
(2)通过对不同均质度黏土劈裂注浆进行数值模拟,得出不同均质度条件下的裂缝发展规律及浆液压力的变化趋势为:随着均质度的增大,土体更难以劈裂,劈裂后产生的裂缝较为单一,裂缝分布范围较小,而均质度较低的土体更容易被劈裂,产生的裂缝宽度较大,裂缝影响范围更为广泛。
(3)针对渗透系数对土体劈裂过程中浆脉长度及宽度的影响分析表明:渗透系数较大土体浆脉扩展的长度较大,浆脉长度增幅较低;距离注浆孔越远,浆脉的宽度越小;渗透系数较大土体的劈裂浆脉宽度要大于渗透系数较小的土体。
-
表 1 现场孔隙率勘探值
Table 1 Field porosity exploration value
TK1 TK2 TK3 TK4 TK5 TK6 勘探深度/m 孔隙率 勘探深度/m 孔隙率 勘探深度/m 孔隙率 勘探深度/m 孔隙率 勘探深度/m 孔隙率 勘探深度/m 孔隙率 0 0.45 0 0.44 0 0.46 0 0.50 0 0.40 0 0.46 1.20 0.26 0.55 0.41 0.40 0.48 1.11 0.49 0.96 0.36 0.46 0.26 1.53 0.28 1.57 0.39 1.21 0.31 1.56 0.38 1.58 0.44 2.29 0.39 3.19 0.26 1.75 0.28 2.66 0.40 1.98 0.25 2.68 0.33 2.29 0.36 3.81 0.45 3.18 0.25 3.30 0.43 2.89 0.35 3.11 0.42 2.93 0.25 4.80 0.38 3.61 0.27 3.61 0.30 3.21 0.35 3.26 0.25 3.06 0.33 5.35 0.49 4.25 0.35 3.92 0.35 3.84 0.37 4.88 0.29 3.72 0.44 5.71 0.47 5.28 0.39 4.09 0.43 4.91 0.29 5.19 0.34 3.84 0.48 6.24 0.39 6.30 0.48 4.30 0.27 5.98 0.45 5.78 0.35 4.36 0.31 6.53 0.26 6.35 0.34 5.28 0.45 6.63 0.39 6.58 0.32 5.66 0.39 表 2 土体物理指标参数
Table 2 Physical index parameters of soil
力学参数 参数值 力学参数 参数值 均质度 1, 2, 4, 6, 8 泊松比 0.35 弹性模量/Pa 由地层不同孔隙率
参数值确定孔隙水压力系数 0.5 黏聚力/MPa 0.02 细观抗压强度/MPa 0.5 内摩擦角/° 22 初始有效压力/MPa 0 渗透系数/(m·d−1) 0.50, 0.05 单步增量/MPa 0.01 -
[1] 张连震, 刘人太, 张庆松, 等. 软弱地层劈裂–压密注浆加固效果定量计算方法研究[J]. 岩石力学与工程学报,2018,37(5):1169-1184 ZHANG Lianzhen, LIU Rentai, ZHANG Qingsong, et al. Calculation of reinforcement effect of fracturing-compaction grouting in soft strata[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(5): 1169-1184. (in Chinese)
[2] 高伟杰, 王建华, 田兆丰, 等. 砂土及黏土场地钻井船插桩对临近桩的影响[J]. 水利水运工程学报,2018(5):111-119 GAO Weijie, WANG Jianhua, TIAN Zhaofeng, et al. Influences of spudcan penetration and extraction on adjacent piles in sand and clay[J]. Hydro-Science and Engineering, 2018(5): 111-119. (in Chinese)
[3] 汪恩良, 商舒婷, 田雨, 等. 齐齐哈尔地区粉质黏土冻胀特性试验研究[J]. 水利水运工程学报,2020(4):80-87 doi: 10.12170/20200106005 WANG Enliang, SHANG Shuting, TIAN Yu, et al. Experimental study on frost heaving characteristic of silty clay in Qiqihar region[J]. Hydro-Science and Engineering, 2020(4): 80-87. (in Chinese) doi: 10.12170/20200106005
[4] 李志鹏. 断层软弱介质注浆扩散加固机理及工程应用[D]. 济南: 山东大学, 2015. LI Zhipeng. Mechanism of grouting spread and reinforcement on soft medium in fault and its application[D]. Jinan: Shandong University, 2015. (in Chinese)
[5] 王哲, 龚晓南, 程永辉, 等. 劈裂注浆法在运营铁路软土地基处理中的应用[J]. 岩石力学与工程学报,2005,24(9):1619-1623 doi: 10.3321/j.issn:1000-6915.2005.09.025 WANG Zhe, GONG Xiaonan, CHENG Yonghui, et al. Application of fracturing grouting method to treat soft foundation of operating railway[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(9): 1619-1623. (in Chinese) doi: 10.3321/j.issn:1000-6915.2005.09.025
[6] 唐亚周, 雷进生, 马波, 等. 不同均质度的黏土劈裂注浆特性及效果分析[J]. 地下空间与工程学报,2020,16(2):547-554 TANG Yazhou, LEI Jinsheng, MA Bo, et al. Study on clay split grouting with different homogeneity and its effect[J]. Chinese Journal of Underground Space and Engineering, 2020, 16(2): 547-554. (in Chinese)
[7] 雷进生, 刘非, 王乾峰, 等. 非均质土层的注浆扩散特性与加固力学行为研究[J]. 岩土工程学报,2015,37(12):2245-2253 doi: 10.11779/CJGE201512014 LEI Jinsheng, LIU Fei, WANG Qianfeng, et al. Diffusion characteristics and reinforcement mechanics of grouting in non-homogeneous soil strata[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(12): 2245-2253. (in Chinese) doi: 10.11779/CJGE201512014
[8] 雷进生, 夏磊, 王乾峰, 等. 非均质地层地质剖面的随机预测模型[J]. 地下空间与工程学报,2016,12(1):84-89 LEI Jinsheng, XIA Lei, WANG Qianfeng, et al. Random prediction model of geological section for non-homogeneous formation[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(1): 84-89. (in Chinese)
[9] 巫尚蔚, 杨春和, 张超, 等. 基于Weibull模型的细粒尾矿粒径分布[J]. 重庆大学学报,2016,39(3):1-12 doi: 10.11835/j.issn.1000-582X.2016.03.001 WU Shangwei, YANG Chunhe, ZHANG Chao, et al. Particle size distribution of fine-grained tailings based on Weibull distribution[J]. Journal of Chongqing University, 2016, 39(3): 1-12. (in Chinese) doi: 10.11835/j.issn.1000-582X.2016.03.001
[10] 蒋浩鹏, 姜谙男, 杨秀荣. 基于Weibull分布的高温岩石统计损伤本构模型及其验证[J]. 岩土力学,2021,42(7):1894-1902 JIANG Haopeng, JIANG Annan, YANG Xiurong. Statistical damage constitutive model of high temperature rock based on Weibull distribution and its verification[J]. Rock and Soil Mechanics, 2021, 42(7): 1894-1902. (in Chinese)
[11] 龙尧, 张家生, 陈俊桦. 基于Weibull分布的土-结构接触面剪切损伤模型研究[J]. 公路交通科技,2017,34(5):65-71 LONG Yao, ZHANG Jiasheng, CHEN Junhua. Study on shear damage model for soil-structure interface based on Weibull distribution[J]. Journal of Highway and Transportation Research and Development, 2017, 34(5): 65-71. (in Chinese)
[12] 唐亚周. 膨胀性浆液劈裂注浆的抬升效应分析[D]. 宜昌: 三峡大学, 2019. TANG Yazhou. Analysis of lifting effect of expansive cement slurry in splitting grouting[D]. Yichang: China Three Gorges University, 2019. (in Chinese)
[13] 雷进生, 武增琳, 姚奇, 等. 基于Weibull分布的非均质地层物性参数随机模型[J]. 地下空间与工程学报,2017,13(3):684-691 LEI Jinsheng, WU Zenglin, YAO Qi, et al. Rand model of heterogeneous formation physical parameters based on Weibull distribution[J]. Chinese Journal of Underground Space and Engineering, 2017, 13(3): 684-691. (in Chinese)
[14] 雷进生. 碎石土地基注浆加固力学行为研究[D]. 武汉: 中国地质大学, 2013. LEI Jinsheng. Research on mechanical behavior of grout in gravelly soil foundations[D]. Wuhan: China University of Geosciences, 2013. (in Chinese)
[15] 马波, 雷进生, 涂保林, 等. 膨胀复合浆液的物理力学性能试验研究[J]. 水利水运工程学报,2020(3):92-98 doi: 10.12170/20190227002 MA Bo, Lei Jinsheng, TU Baolin, et al. Experimental study on physical and mechanical properties of expanded composite slurry[J]. Hydro-Science and Engineering, 2020(3): 92-98. (in Chinese) doi: 10.12170/20190227002
[16] 冉启全, 李士伦. 流固耦合油藏数值模拟中物性参数动态模型研究[J]. 石油勘探与开发,1997,24(3):61-65, 100 doi: 10.3321/j.issn:1000-0747.1997.03.015 RAN Qiquan, LI Shilun. Study on dynamic models of reservoir parameters in the coupled simulation of multiphase flow and reservoir deformation[J]. Petroleum Exploration and Development, 1997, 24(3): 61-65, 100. (in Chinese) doi: 10.3321/j.issn:1000-0747.1997.03.015
[17] 程少振. 土体劈裂注浆扩散与加固机理及工程应用[D]. 北京: 北京交通大学, 2019. CHENG Shaozhen. Study on propagation and reinforcement mechanic of fracture grouting in soil and its engineering application[D]. Beijing: Beijing Jiaotong University, 2019. (in Chinese)
[18] 李永乐, 刘翠然, 刘海宁, 等. 非饱和土的渗透特性试验研究[J]. 岩石力学与工程学报,2004,23(22):3861-3865 doi: 10.3321/j.issn:1000-6915.2004.22.023 LI Yongle, LIU Cuiran, LIU Haining, et al. Testing study on permeability characteristics of unsaturated soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(22): 3861-3865. (in Chinese) doi: 10.3321/j.issn:1000-6915.2004.22.023
[19] 孙大松, 刘鹏, 夏小和, 等. 非饱和土的渗透系数[J]. 水利学报,2004,35(3):71-75 doi: 10.3321/j.issn:0559-9350.2004.03.012 SUN Dasong, LIU Peng, XIA Xiaohe, et al. Permeability coefficient of unsaturated soils[J]. Journal of Hydraulic Engineering, 2004, 35(3): 71-75. (in Chinese) doi: 10.3321/j.issn:0559-9350.2004.03.012
-
期刊类型引用(3)
1. 秦鹏飞,钟宏伟,刘坚,苏丹娜,孙卓宇. 考虑浆土应力耦合作用的劈裂注浆机理分析. 西南交通大学学报. 2023(03): 584-591 .  百度学术
百度学术
2. 李晓龙,陈坤洋,陈灿,李媛媛,钟燕辉,张蓓,王复明. XFEM和修正剑桥模型模拟高聚物劈裂注浆方法研究. 水力发电学报. 2023(07): 24-36 .  百度学术
百度学术
3. 张祥富,黄松,李永丰,胡栋,孙谞,李建中. 适应于强风化花岗岩地层注浆的超细颗粒浆液研究. 工业建筑. 2023(S2): 421-424+417 .  百度学术
百度学术
其他类型引用(4)



 Email Alerts
Email Alerts RSS
RSS
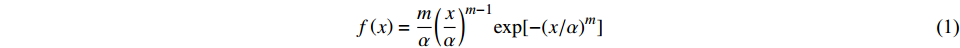
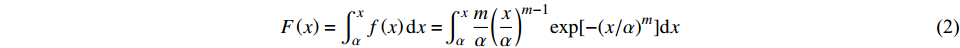
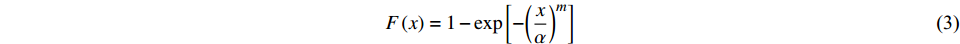
 下载:
下载: