地下水封石油洞库容积较大，主要存储低凝轻质原油，在洞库进出油作业过程中会产生和挥发大量的油气^[1]。地下水封石油洞库表面的边界条件不同于其他岩土领域，洞室不仅包含一层液体油，而且还包含油层下方的水垫层和油层上方的油气层^[2]。在储油期，液体油位和油蒸气压的变化频繁，油、水、油气密度的不同导致洞室壁压力呈分段线性分布^[3]。为保障储油洞库的正常运行，油层以上的洞壁和洞顶要始终保持适度的油气压力，这种油气压力由产生的油蒸气与注入的氮气组成^[4]。相比于液态油体，油气的低黏度使其更容易通过周围岩石的裂隙和孔隙扩散。如果油气压或围岩渗透性足够高，油气可能进入水幕孔或突破地下水位，增加泄漏的风险^[5]。Li等^[4]考虑洞库油气压的影响，对洞库附近的地下水渗流场进行了三维模拟分析，发现洞室内的油气压力会影响地下水渗流场，在洞室附近产生一定范围的油气侵入区，影响洞室涌水量。油气压力对渗流场的影响主要体现在油气泄漏与洞室涌水量的变化两个方面。

国内外相关学者根据洞室附近水力梯度或压力梯度的关系提出了控制气体泄漏的标准^[6-9]，并从洞库渗流场的角度研究了水幕系统的水封效果^[10-11]。但这些研究仅从水力梯度与压力的角度进行单一相的研究，并未考虑多相流体的运移规律。近年来，随着多相流理论的发展^[12-13]，许多学者采用数值模拟方法揭露油气泄漏的机理。Yamamoto等^[14]基于日本某地下储油洞库，建立了考虑渗透系数随机性的二维三相流模型，模拟了洞库气体泄漏现象，并讨论了洞库的储存安全性及气体泄漏的潜在原因；Hu等^[15-16]建立了基于THOUGH2的二维三相流模型，研究了不同水幕压力作用下储存产品的泄漏规律及水幕压力与储气压力的关系，确定了所对应案例下水幕压力的合理范围；唐栋等^[17]利用有限元软件对不同水幕压力与不同水封厚度下的油气运移规律进行研究，确定了合适的水封厚度。洞室涌水量控制与预测是地下水封石油洞库的重点研究方向。时洪斌等^[18]通过开挖工况和运行工况的渗流场数值模拟，估算了某地下水封石油洞库的涌水量，并系统研究了该石油洞库的水封性能；Wang等^[19-20]利用经验公式、有限元公式研究了地下水封石油洞库水流入的尺度和空间分布特征，为水幕系统的设计提供了有益参考；蒋中明等^[21]提出了一种基于嵌入裂隙单元模型（EFE模型）的裂隙岩体渗流分析方法，建立了涌水量预测模型，并与工程实测资料进行对比，证明了EFE模型的可行性；Xu等^[22-23]在回归分析的基础上研究了洞室涌水量对各种水幕孔参数的敏感性，提出了一种储油洞库地下水密封评价方法。

可见，国内外已开展的有关洞库油气泄漏与涌水量调节方面的研究，主要集中在油气泄漏机理和水幕参数的优化上，很少考虑油气压力对渗流场的影响。当洞室附近油气压力大于周围的水压时，洞库顶部积聚的油气会泄漏到围岩甚至大气中，对环境产生极大危害^[24-26]。此外，由于水封洞库独特的存储机制，施工期和运行期都会有地下水渗入洞库，以往的研究多关注施工期洞室开挖及运行期不同水幕参数对涌水量的影响，很少有人研究运行期油气压力对洞室涌水量的影响。本文采用有限元数值模拟方法，以某石油储备地下水封洞库为依托，考虑油气压力对渗流场的影响，采用多物理场耦合软件COMSOL Multiphysics模拟地下水封石油洞库储油运行期在不同油气压力下的地下水位、油气泄漏及洞室涌水量的变化规律，以及洞库不同油位对涌水量的影响，确定合理的油气压力。研究成果可为水封油库洞室顶部油气压力的调控提供参考。

1.   数值模拟理论与方法

地下水在洞库周围缓慢流动，满足达西定律。地下水流动的控制方程为：

式中：$ \rho $为水的密度（kg/m³）；S_p为储水系数（1/Pa）；p为孔隙水压力（Pa）；Q_m为质量源项（kg/(m³·s)）；$\mu_{\mathrm{w}} $为水的动力黏度（Pa·s）；$ u $为流速（m/s）；k为岩体渗透率（m²）；g为重力加速度（m/s²）。

洞室涌水量可以通过对速度积分来计算。由于油气与水不相容，不同油气压力下的油气泄漏可以基于气-液两相流理论模型进行描述。两相的质量守恒方程由多孔介质相传递接口给出，其控制方程为：

式中：$ \varepsilon_{\mathrm{p}} $为孔隙率；$ k\mathrm{_{rsw}} $和$ k\mathrm{_{rsg}} $分别为水和气的相对渗透率；$ k $为多孔介质的渗透率 ；$ \rho_{\mathrm{w}}\mathrm{和}\rho_{\mathrm{g}} $为水和气的密度（$ \mathrm{k}\mathrm{g}/{\mathrm{m}}^{3} $）；$ \mu_{\mathrm{w}} $和$ \mu_{\mathrm{g}} $分别为水相与气相的动力黏度（Pa·s）；$ s\mathrm{_w} $和$ s_{\mathrm{g}} $为水相和气相的饱和度，满足$ s_{\mathrm{w}}+s\mathrm{_g}=1 $。

毛细压力模型选取Brooks-Corey模型，两相的相对渗透率为：

式中：$ \overline{s_{\mathrm{w}}} $与$ \overline{s_{\mathrm{g}}} $分别为平均水、气相饱和度；$ s_{\mathrm{rw}} $和$ s_{\mathrm{rg}} $分别为水、气相的残余饱和度；$ \lambda_{\mathrm{p}} $为Brooks-Corey模型的孔隙分布指数。

为模拟不同油气压力作用下的洞室油气泄漏规律及涌水量的变化规律，使用COMSOL Multiphysics有限元模拟软件的多孔介质多相流耦合接口，将达西定律与多孔介质相传递物理场进行耦合求解，方程为：

式中：$ \overline{\rho } $为流体的平均密度（$ \mathrm{k}\mathrm{g}/{\mathrm{m}}^{3} $）；i取水相(w)与气相(g)；$ \overline{\mu } $为流体平均动力黏度（Pa·s）。

2.   油气压力数值模拟

某地下水封石油洞库的设计库容为500×10⁴ m。洞库区分成4组洞罐，每组洞罐2个洞室，每2个主洞室之间通过连接巷道组成一个罐体，主洞室断面为直墙圆拱，跨度为20 m、高度30 m，洞顶高程−80 m，底板高程−110.00 m。主洞室顶板以上25 m处设置水幕系统 ^[27]。

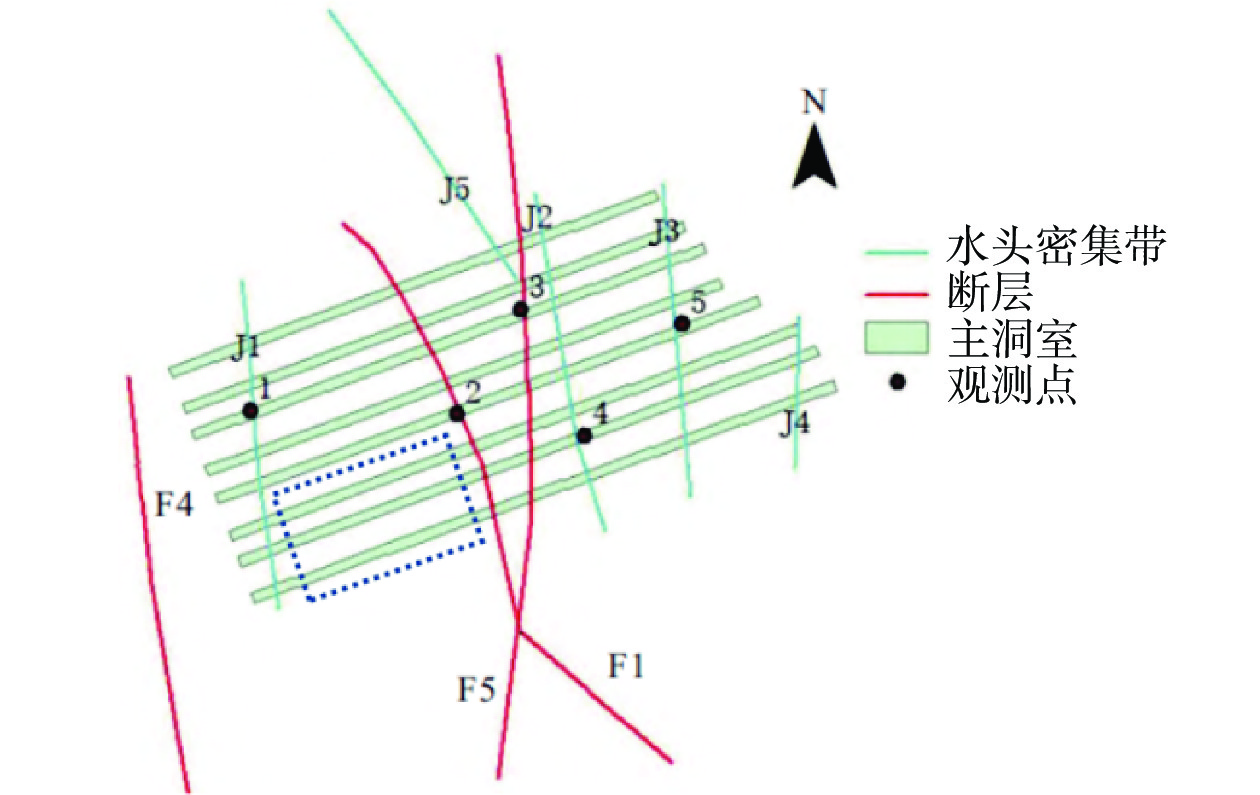
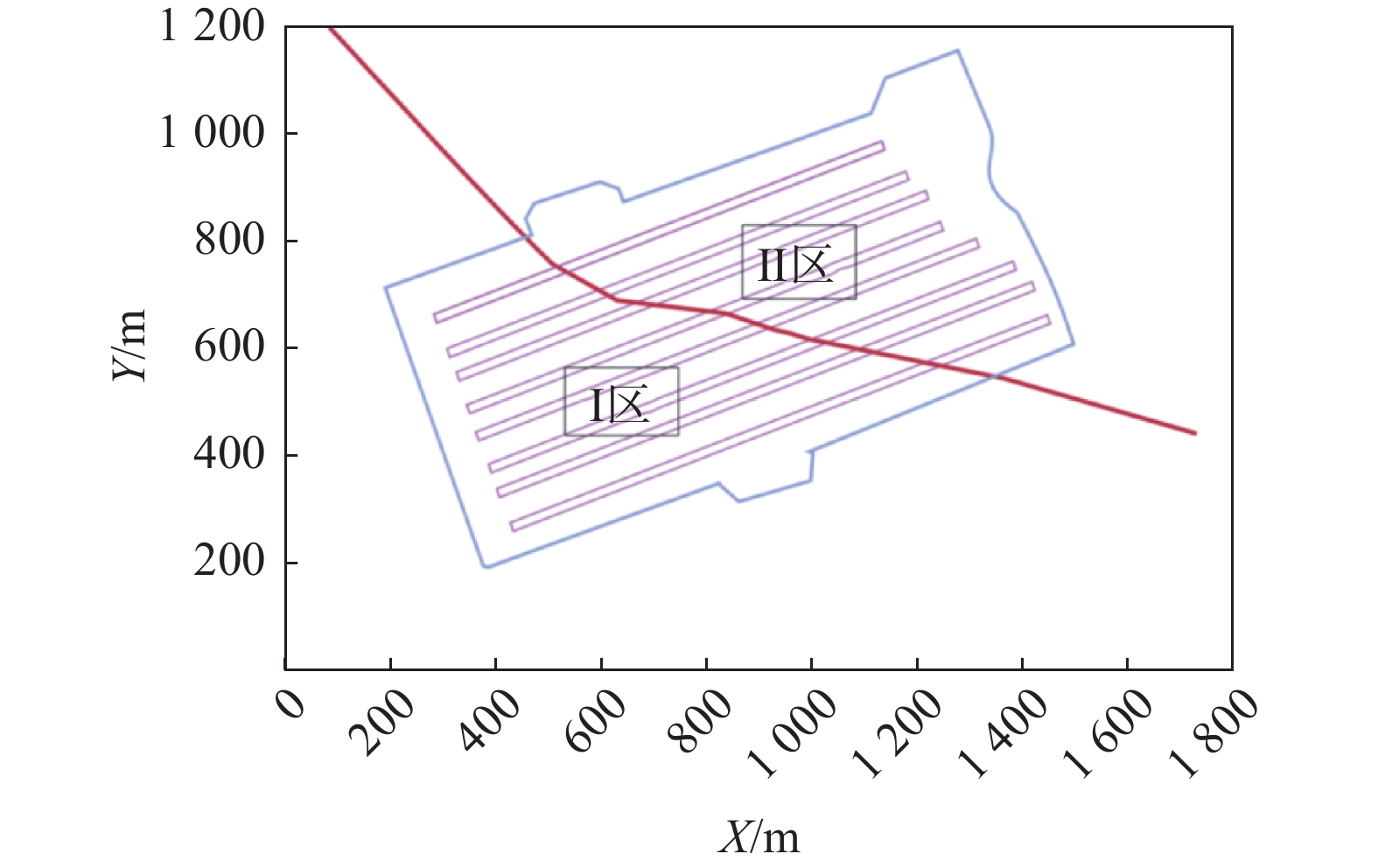
库址区内的含水介质主要是燕山期细粒二长花岗岩、中细粒正长花岗岩和第四纪覆盖层，根据场地钻孔水位观测资料及场地外围水文地质调查资料，场地内水位标高为12~122m。为分析库区不同深度岩体渗透系数及其分布规律，勘察布置若干水文地质试验孔，以压水试验为主，脉冲和注水试验为辅，获得了试验钻孔中渗透系数分布特征。孔内试验成果显示试验段渗透系数与深度、标高无明显关系，超过72%的试验段渗透性等级为极微透水，总体上反映了岩体的低渗透性。通过分析库区水幕层和主洞室层渗透系数空间分布特征，可知场区内渗透系数具有分区现象，按照区内相似、各区间相异的原则，将整个库区划分为两个区（见图1）。为提高数值模拟计算结果的准确性，根据库区渗透系数分布特征、钻探和物探成果及综合考虑现场地形与地质构造的分布情况，Ⅰ区取等效渗透系数为8.5×10⁻⁴ m/d，Ⅱ区为1.1×10⁻³ m/d。

图  1  渗透系数分区示意

Figure  1.  Schematic diagram of permeability coefficient partition

下载: 全尺寸图片 幻灯片

图2为库区地质构造图^[27]，本文主要研究地下水封石油洞库在储油期不同油气压力下的油气泄漏及涌水量变化规律，在施工期已对断层、节理密集带等导水结构层及时注浆堵漏，因此，为简化计算，忽略断层、节理密集带等导水结构层的影响。由于库区西南侧岩石完整性好，可以更好地反映油气压力变化对渗流场的影响，因此计算模型取自位于库区西南侧的相邻3个洞室，见图2框选部分。采用多物理场耦合软件COMSOL Multiphysics建立二维等效连续介质模型。

图  2  库区地质构造图^[27]

Figure  2.  Geological structure map of the storage area^[27]

下载: 全尺寸图片 幻灯片

模型模拟范围长282 m、高180 m，由3个储油洞室及水幕系统组成，计算网格单元数为47 657。左右边界距两侧洞室外侧距离均为65 m，底部边界至洞底距离为40 m，洞室之间距离分别为57、35 m。主洞室顶板以上25 m处设置水幕系统（图3）。对于地下水渗流边界条件，模型左右边界为压力边界条件，顶、底部为无流动，水幕孔压力为0.3 MPa，以洞室开挖3年后的静水压力场为初始值。本文算例中，忽略水垫层的厚度，洞库拱顶、侧壁和底板边界根据油气压力、储油压力分别施加。对于两相传递场的边界条件，模型左右边界、水幕孔为液相边界，洞库顶拱设为气相边界；考虑油气主要积聚在洞室顶部，本文主要研究不同油气压力下的油气泄漏。因此，洞库侧壁、底板按液相边界设置。模型底部边界为无通量边界，考虑油气有可能进入大气，模型顶部边界设为流出边界。模型计算区域位于洞室西南侧，由于岩体整体渗透性较低，渗透系数与深度、标高无明显关系，选用等效连续介质模型可以反映整体渗透性，因此根据库区岩土工程勘察报告选取等效渗透系数为$ 8.5\times {10}^{-4}\mathrm{m}/\mathrm{d} $，孔隙率$ {\mathrm{\varepsilon }}_{\mathrm{p}} $为0.05。流体参数参考相关文献^[28]，取水密度$ {\mathrm{\rho }}_{\mathrm{w}} $为1 000 $ \mathrm{k}\mathrm{g}/{\mathrm{m}}^{3} $，水动力黏度$ {\mathrm{\mu }}_{\mathrm{w}} $为0.001 Pa·s，油气密度$ {\mathrm{\rho }}_{\mathrm{g}} $为3.125 $ \mathrm{k}\mathrm{g}/{\mathrm{m}}^{3} $，油气动力黏度为$ 2\times {10}^{-5} $ Pa·s，油品密度为850 $ \mathrm{k}\mathrm{g}/{\mathrm{m}}^{3} $。通过调整油气压力大小，可以获取不同油气压力下的地下水位、油气泄漏与洞室涌水量的变化规律。对洞库经3 a施工期后在储油运行50 a的情况进行分析，设定工况1~8对应的油气压p_g分别为0.05、0.10、0.15、0.20、0.25、0.30、0.35、0 MPa。

图  3  计算模型网格划分

Figure  3.  Grid division of the computational model

下载: 全尺寸图片 幻灯片

3.   不同油气压力下的渗流场分析

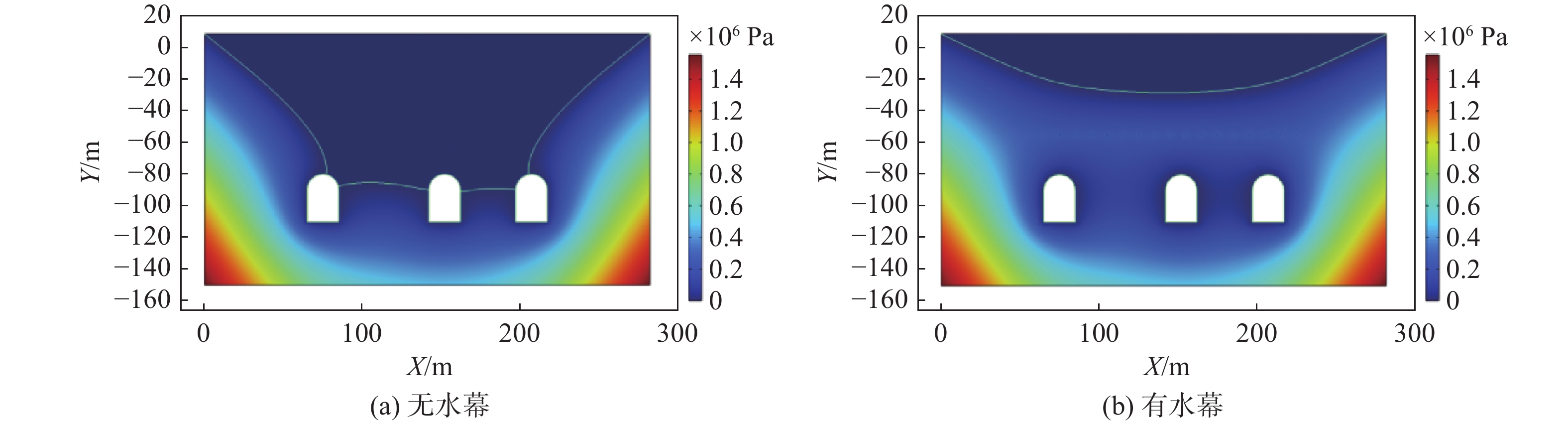
地下洞室的开挖会改变洞库区的渗流场分布，在研究储油期油气压力对渗流场的影响时，需要考虑施工开挖后洞室的地下水位与孔隙水压力的分布。图4为施工期在无水幕与有水幕系统下洞室开挖3 a后的孔隙水压力与地下水位分布。可见，洞室开挖后，洞顶上方的水位下降形成了一个降落漏斗。无水幕时，洞室开挖导致洞顶上方水迅速疏干，洞顶直接与大气接触，此时储油后会发生油气外溢；有水幕系统时，由于水幕系统的补水作用，洞顶上方的水位下降幅度较小，阻止了大规模降落漏斗的形成，可保证洞室的水封性能。因此，为了确保洞室的水封效果，防止油气外溢，需要在洞室上方设置水幕系统。

图  4  洞室开挖3 a后的孔隙水压与地下水位分布

Figure  4.  Pore water pressure and groundwater level distribution of the chamber after 3 a excavation

下载: 全尺寸图片 幻灯片

图5为洞室顶部无油气压（0 MPa）与有油气压（0.35 MPa）的地下水位。可见洞室顶部的油气压力会对地下水位的高度产生影响，这说明油气压力会影响洞室周围渗流场。图6为不同油气压力下的地下水位至水幕的距离。由图6可知，相比于无油气压力的情况，油气压力会使地下水位上升，且随着油气压力的增大，地下水位至水幕的距离由26.88 m增至31.22 m，呈线性增大。这说明在储油运行期，洞室顶部的油气压力会对渗流场产生一定影响，当油气压力增加时，地下水位升高，有利于减少地下水的损失。

图  5  不同油气压力下的地下水位

Figure  5.  Groundwater levels under different oil and gas pressures

下载: 全尺寸图片 幻灯片

图  6  不同油气压力下地下水位至水幕的距离

Figure  6.  Distance from groundwater level to water curtain under different oil and gas pressures

下载: 全尺寸图片 幻灯片

本文从油气压力与油气泄漏量和洞室涌水量的变化关系出发，通过调整油气压力，获取不同油气压力下的油气泄漏及涌水量变化规律，从而评估油气压力变化对渗流场的影响程度。

3.1   油气压力对油气泄漏的影响分析

为保障洞库的正常运行，洞室顶部需要维持一定的气体压力，控制油气泄漏在一定范围内的同时使涌水量最小的气体压力为临界气体压力。当洞室内的油蒸气压力未达到临界气体压力时，需注入氮气，此时洞室的气体由油蒸气与氮气组成；当洞室内的油蒸气压力超过临界气体压力时，需向外抽取油蒸气。对于油气泄漏而言，由于氮气属于惰性气体，对环境较为友好；当洞室顶部的油气全为油蒸气时，为最不利的情况。因此，进行油气泄漏模拟时，将洞室顶部的油气视为油蒸气。

图7为储油期不同油气压力下50 a后的油气饱和度云图。洞室顶部存在油气压时，便在洞顶上方一定范围处形成油气泄漏区，随着油气压力的增大，油气不断向外扩散，泄漏区面积不断增加。当油气压力小于0.20 MPa时，油气向上泄漏控制在一定范围内，保证了水封有效性，见图7(a)~图7(d)；而当油气压力超过0.20 MPa时，油气迅速向上扩散，扩散至水幕孔，导致水幕系统失效，水封失效，见图7(e)；随着油气压力的继续扩大，油气继续向上泄漏，直至泄漏至地下水位，导致大量油气在地表附近聚集及进入大气，对环境产生严重污染与危害，见图7(f)~图7(g)。

图  7  不同工况下50 a后油气饱和度分布云图

Figure  7.  Saturation distribution cloud map of oil and gas after 50 a under different working conditions

下载: 全尺寸图片 幻灯片

为了计算不同油气压下的油气泄漏量，采用唐栋等^[17]定义的油气泄漏量公式：

式中：$ {s}_{\rm g} $为油气相的体积分数；$ {\varepsilon }_{\rm p} $为孔隙率。

图8为不同油气压下油气泄漏量与竖向泄露距离。由图8可知，当油气压小于0.20 MPa时，油气泄漏量从13.27 m²增至17.00 m²，平均增速为13.36%，趋势较为平缓；竖向泄露距离从11.54 m增至18.67 m，小于水封厚度25 m，水封性好。油气压达0.25 MPa后，油气泄漏量从17 m²迅速增至42.1 m²，增速高达148.12%；竖向泄漏距离从18.67 m增至43.23 m，超过水封厚度，水封性能失效。随着油气压力的继续增大，油气泄漏量迅速增加，竖向泄漏距离增至88.64 m，油气泄漏至地面。图9为竖向泄漏距离的拟合曲线。由图9可知，竖向泄漏距离随油气压的增大呈指数函数分布。根据拟合公式得到，竖向泄漏距离为25 m时，对应的油气压力为0.21 MPa。因此当油气压小于0.21 MPa时，在水幕系统的作用下，竖向泄漏距离小于水封厚度，使油气泄漏量控制在一定范围内，满足水封性。而当油气压超过0.21 MPa后，洞室附近的水压小于油气压，油气迅速向上扩散，超过水封厚度，导致水封性能失效，油气泄漏量迅速增加。由此可见，应控制洞库内的油气压力，因为油气压力的增加可能会扩大油气泄漏区，突破洞室以上的水封厚度，增大泄漏风险。当地下水封石油洞库运营期水幕压力为0.30 MPa时，为了保证水封安全，防止油气泄漏，应控制洞室油气压小于0.21 MPa。

图  8  不同油气压下的油气泄漏量与竖向泄漏距离

Figure  8.  Oil and gas leakage amount and vertical leakage distance under different oil and gas pressures

下载: 全尺寸图片 幻灯片

图  9  不同油气压下的竖向泄漏距离拟合曲线

Figure  9.  Fitted curve of vertical leakage distance under different oil and gas pressures

下载: 全尺寸图片 幻灯片

3.2   油气压对洞室涌水量的影响分析

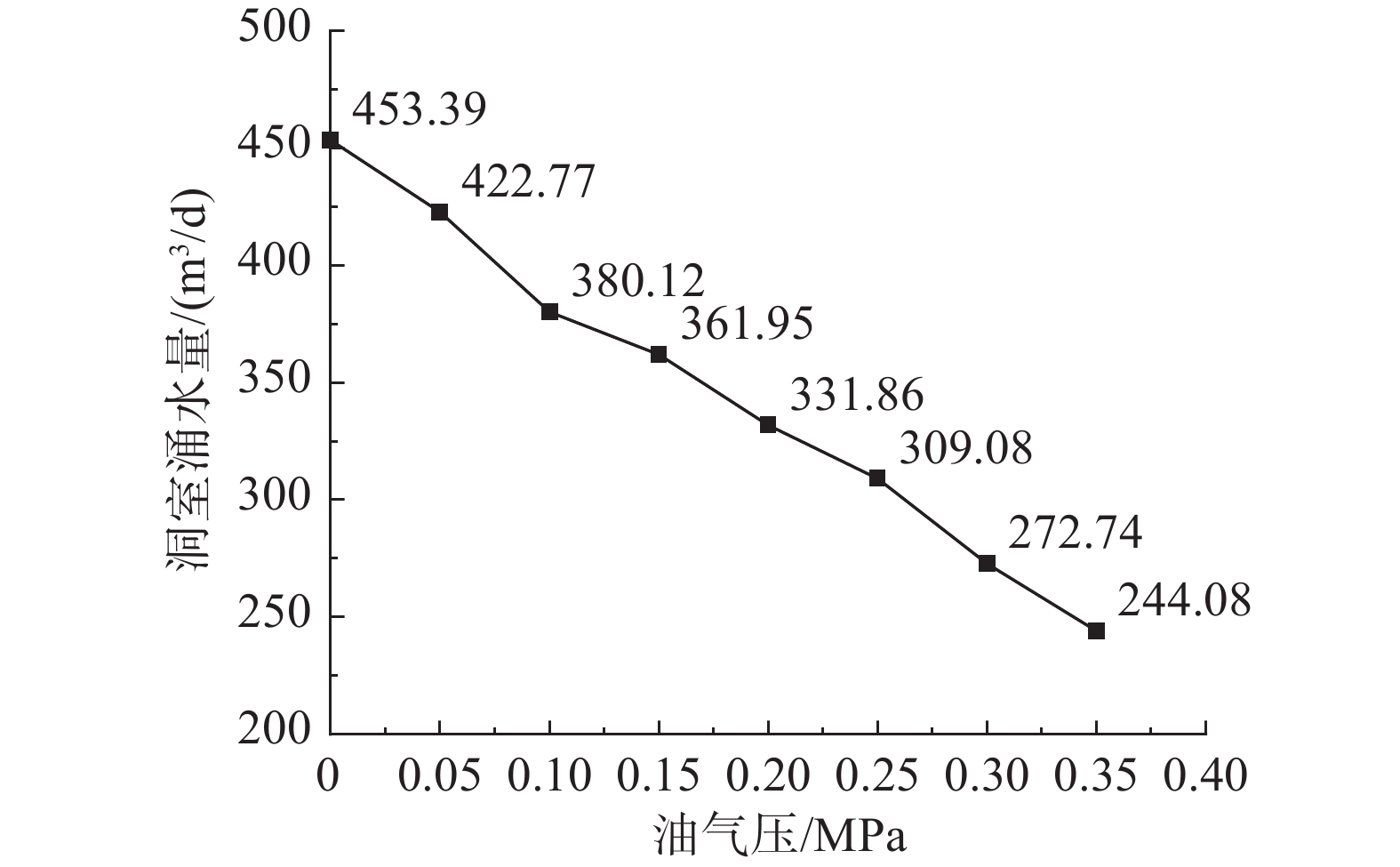
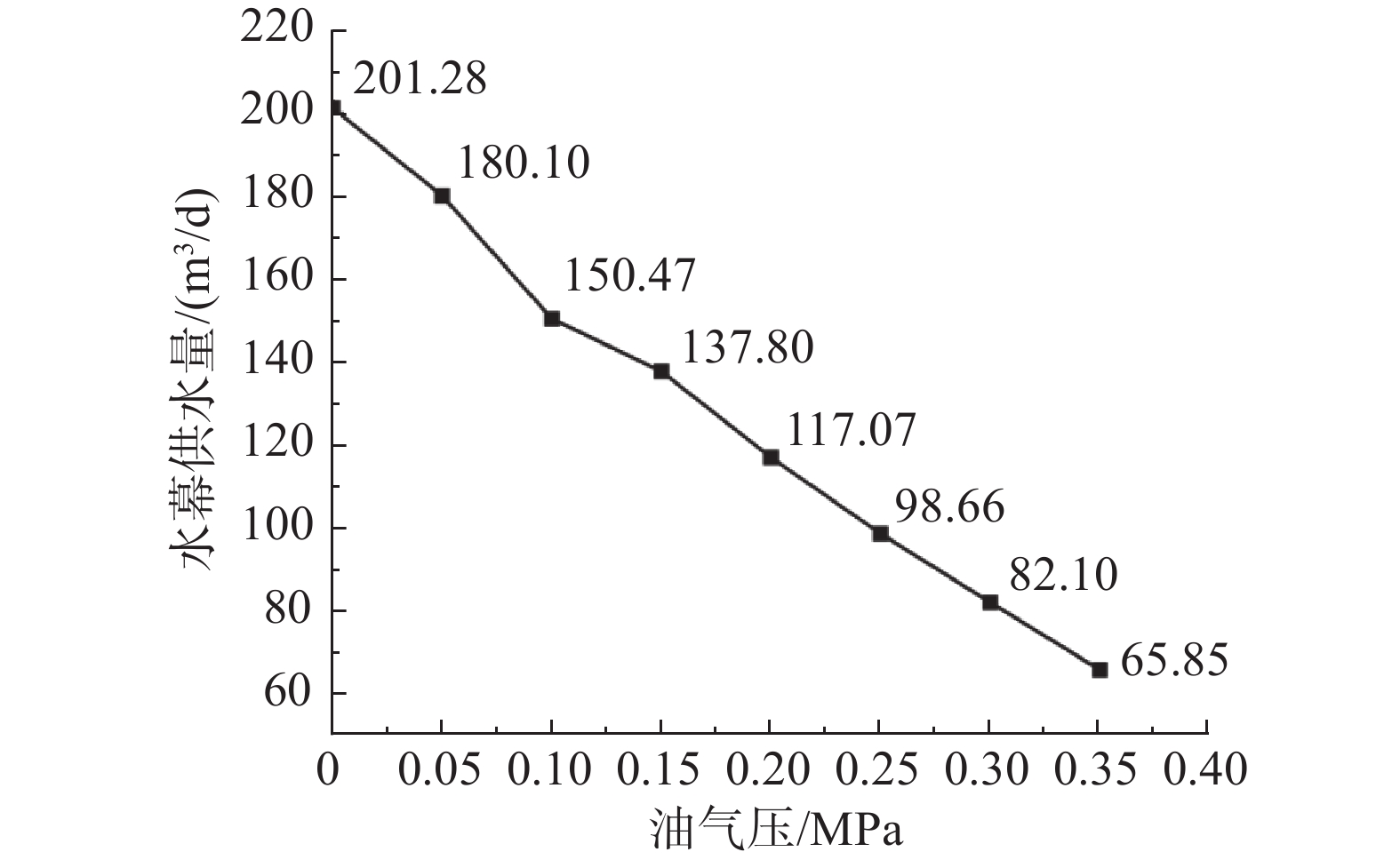
洞室顶部油气压力会对渗流场产生影响。图10~11为不同油气压下的主洞室涌水量与水幕供水量。可见随着油气压力的增加，洞室涌水量呈线性下降趋势。对比洞室顶部没有油气压力的工况，发现洞室存在油气压力时，会显著降低洞室内的涌水量，随着油气压的增加，洞室涌水与水幕注水量逐渐减少，对比油气压力为0与0.2 MPa，洞室涌水量从453.4 m³/d降低到331.9 m³/d。这说明洞室顶部的油气压力有助于维持油库的压力平衡，可以有效防止因地下水压力过大而导致的过多洞室涌水量，从而降低水幕注水成本。单从洞室涌水量的角度看，油气压力越大，水幕供水与洞室涌水量越小，能降低生产成本，经济效益越好。但油气压过大会导致油气迅速泄漏，导致水封性能失效。

图  10  不同油气压下的洞室涌水量

Figure  10.  Water inflow into the cavern under different oil and gas pressures

下载: 全尺寸图片 幻灯片

图  11  不同油气压下的水幕供水量

Figure  11.  Water supply of the water curtain under different oil and gas pressures

下载: 全尺寸图片 幻灯片

在洞室储油运行过程中，油位不时变化，通过调节油气压力，可以控制洞库中的油位，便于储油产品的提取和注入。洞室内油气的体积不断变化，会对洞室涌水量产生影响。为了研究洞室内油气体积对水封安全及洞室涌水量的影响，模拟了0.2 MPa油气压下，5、10、15、20、25 m处不同油位时对应的洞室涌水量。

不同油位下的洞室涌水量和水幕供水量见表1。可见，油气压为0.2 MPa时，随着洞室内油位从5 m上升到25 m，洞室总涌水量从387.48 m³/d降低到314.04 m³/d，而水幕系统供水量从124.03 m³/d降低到112.16 m³/d，说明高运行油位使洞室涌水量与水幕供水量降低，洞室抽水与水幕注水成本随之降低。与洞室内气体压力为0 （工况F）相比，相同油位但油气压为0.2 MPa（工况D）的洞室涌水量降低了104.81 m³/d，水幕供水量降低了84.22 m³/d，这表明洞室顶部的油气压会显著抑制地下水涌入洞室，并减少水幕注水量。油位越高，液态油品体积越大，油气体积越小，对应的洞室涌水量及水幕注水量越小。为了减少洞室抽水的成本，储油产品提取后需要及时补充，以保持相对较高的油位。

表  1  不同油位下洞室涌水量

Table  1.  Cavern water inflow under different oil levels

工况	油位/m	油气压/MPa	水幕供水量/(m3/d)	洞室涌水量/(m3/d)
				洞室1	洞室2	洞室3	全部洞室
A	5	0.2	124.03	151.03	92.51	143.94	387.48
B	10	0.2	122.52	145.97	86.79	138.50	371.25
C	15	0.2	120.29	133.50	76.905	126.11	350.80
D	20	0.2	117.07	133.35	74.674	125.69	333.72
E	25	0.2	112.16	126.16	69.09	118.79	314.04
F	20	0	201.29	180.40	106.31	168.89	455.61

下载: 导出CSV 

| 显示表格

4.   讨　论

地下水封石油洞库油气压力对渗流场的影响体现在两方面：一是油气压力会在洞室周边产生一定范围的油气泄漏区，导致油气扩散，污染水源；二是产生的油气泄漏区会抑制地下水涌入洞室，使地下水位升高，减少运营成本。因此，合理调控油气压力非常重要。

确定合理的油气压力需要同时考虑油库的水封安全和经济成本。使用过小的油气压力，过分强调水封安全将会导致水幕系统供水过多，洞室涌水量大幅增加，从而影响储油能力，产生高昂的成本；而使用过大的油气压力，过分强调洞库的水封经济性，虽会降低水幕系统的运营成本，但可能会导致洞室附近的地下水压力小于油气压力，导致油气泄漏突破水封厚度，增大油气的泄漏量与泄漏范围，污染地下水资源和地表生态环境。

参照Liu等^[29]提出的水封效率计算方法，为保证地下水封石油洞库安全与经济的运行，在确定合理油气压力时同时考虑油气泄漏量A与洞室涌水量Q，建立水封效率量化指标$ {I}_{\rm e} $，以表征单位油气泄漏下的日涌水量，其计算公式见式(14)。已知当油气压力大于0.21 MPa时，竖向泄漏距离超过25 m，大于水封厚度，水封失效，水封量化指标$ {I}_{\rm e} $此时没有意义。因此本文只讨论油气压力小于0.21 MPa时工况。$ {I}_{\rm e} $越小，单位油气泄漏量下日涌水量越小，水封效率越高。

式中：L为洞室长度（m）；t为运行时间（d）。

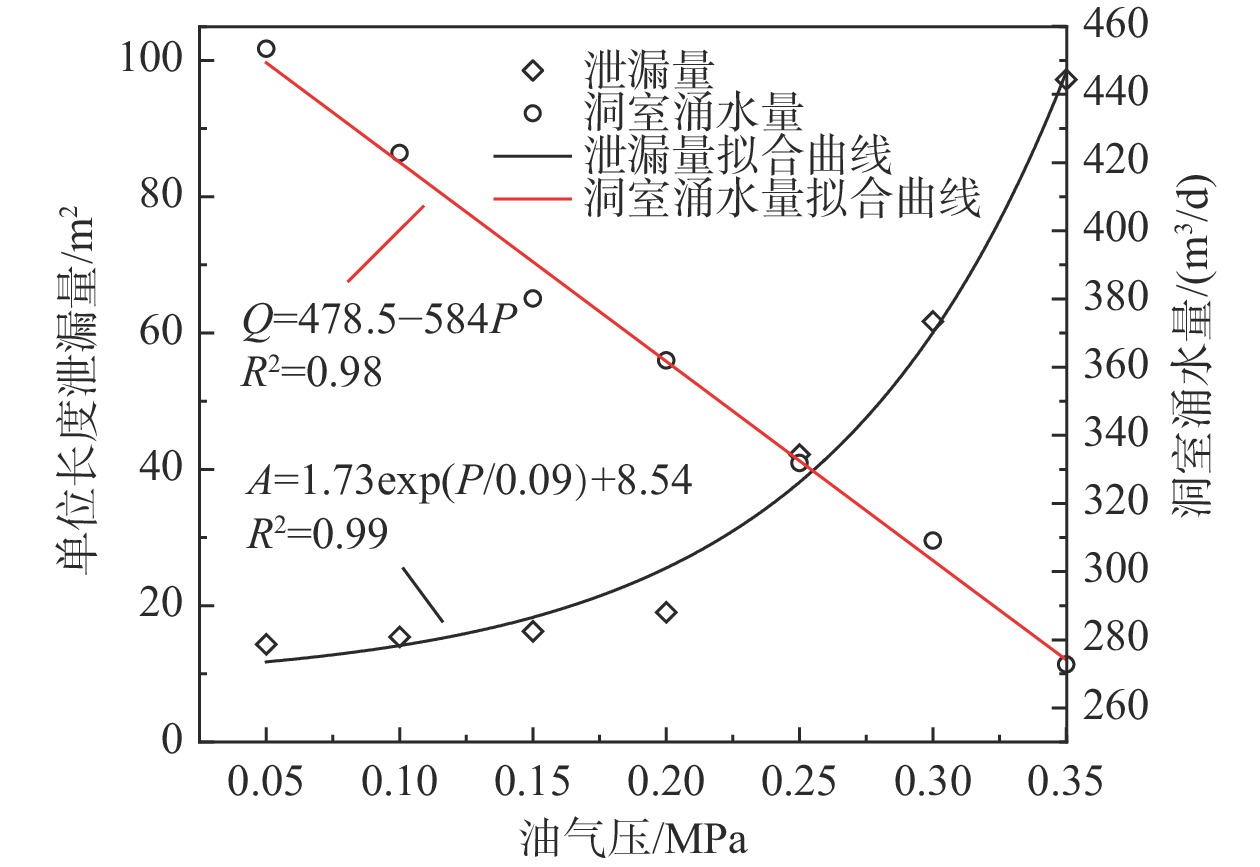
图12为不同油气压下的泄漏量与洞室涌水量拟合曲线。将泄漏量与洞室涌水量拟合方程代入式（14），得到不同油气压力下的水封量化指标（图13）。可见，随着油气压力的增加，水封量化指标$ {I}_{\rm e} $呈线性趋势下降，油气压力为0.21 MPa时，$ {I}_{\rm e} $最小为0.013，但此时竖向泄漏距离为25 m，存在突破水封厚度导致水封失效的可能。因此，为了留有一定的安全裕度，取油气压力为0.20 MPa，此时竖向泄漏距离为18.67 m，水封性能良好。

图  12  不同油气压下的泄漏量与洞室涌水量拟合曲线

Figure  12.  Fitted curve of leakage amount and cavern water inflow under different oil and gas pressures

下载: 全尺寸图片 幻灯片

图  13  不同油气压下的水封量化指标

Figure  13.  Quantitative indicators of water sealing under different oil and gas pressures

下载: 全尺寸图片 幻灯片

本文基于气液两相流理论对地下水封石油洞库在储油期的地下水位的波动、油气泄漏与洞室涌水量变化规律进行了研究，发现本文所对应的案例洞室上方油气压力为0.20 MPa时，可以在经济性的前提下保证水封安全，并留有一定的安全裕度。

5.   结　语

本文依托某地下水封石油洞库工程，基于气液两相流理论，研究了洞室在不同油气压力下的地下水位、油气泄漏与涌水量的变化规律，并分析了不同油位高度对洞室涌水量的影响，得出如下结论：

（1）油气压力会对洞室周围的渗流场产生影响，具体表现为油气压力越大、地下水位越高、洞库周围的油气泄漏范围与泄漏量越大、对应的洞室涌水量与水幕供水量越小。

（2）在洞室储油运行过程中，油位不时变化，不同的油位高度会对洞室涌水量产生影响。油位越高，液态油品体积越大,油气体积越小，对应的洞室涌水量及水幕注水量越小。考虑到油库的水封安全与储油成本，油库应保持较高的油位运行。

（3）水封量化指标$ {I}_{\rm e} $可作为判断水封效率的指标，$ {I}_{\rm e} $越小，对应单位泄漏下的日涌水量最小，水封效率越高。

目前对于油气压力对渗流场影响方面的研究较少，尤其在油气泄露方面的研究往往采用等效连续介质模型，具有一定的局限性。如何建立起三维精细化模型来研究油气压力对油气泄漏的规律，以准确评估油气泄漏量并建立准确的水封量化指标，是进一步研究的一个重要方向。