运河两岸、渠道等水利工程中普遍使用的挡墙为砌石、混凝土、钢筋混凝土等材料建造的刚性挡墙，这类挡墙通常以墙体重力来维持自身的稳定性，因此挡墙墙体体积大，对地基要求也高^[1-4]。20世纪90年代末，采用在挡墙与填土之间设置土工泡沫（简称“EPS”）板来减小挡墙土压力的技术，这种挡墙被称为EPS板减压挡墙^[5]。EPS板减压挡墙利用EPS板的高压缩性，为墙后填土变形提供空间，理论上可有效减少挡墙受到的土压力。为探究EPS板减少挡墙土压力性能，国内外学者对EPS板减压挡墙开展了广泛研究。Ertugrul等^[6-7]通过模型试验研究发现，EPS板减压挡墙利用EPS板的压缩变形，使土压力从静止状态变为主动状态，从而减少由填土自重和上覆荷载引起的作用在墙体上的土压力，混凝土墙体本身的厚度因此可减小，同时降低处理地基的费用；EPS板减少不可动刚性挡墙土压力的效果明显，对可动挡墙和柔性挡墙土压力的减压效果不明显；郑俊杰等^[8]通过数值模拟发现EPS板密度和厚度对其减少刚性挡墙土压力的效果有着显著影响。

土压力是进行挡墙断面设计和稳定验算的重要荷载，Ni等^[9-11]假定在墙后填土上方施加荷载时，EPS板压缩变形从墙顶到墙底呈线性增大，从而推导了EPS板减压挡墙墙后土压力的计算公式，为EPS板减压挡墙的设计提供了科学依据。然而，大量研究结果表明，挡墙墙后土压力沿墙高呈非线性分布^[12-14]。此外，Terzaghi通过活动门试验验证了回填土滑楔体内的土拱效应，土拱效应的存在影响了挡墙墙后土压力的分布和大小^[15]，这说明忽视土拱效应可能导致土压力计算不准确。但以往提出的EPS板减压挡墙土压力计算方法均未考虑土拱效应的影响。为此，本文开展回填土为砂土的EPS板减压挡墙模型试验，研究EPS板减压砂土挡墙位移模式和土压力分布规律；假定墙后回填土滑楔体内土拱形状为圆弧形，基于微分单元法给出考虑土拱效应的EPS板减压砂土挡墙土压力的计算方法，并通过与模型试验结果对比，验证所提出计算方法的合理性；基于该计算方法，最后分析了EPS板厚度和密度对挡墙墙后土压力的影响。

1.   模型试验

1.1   试验概况

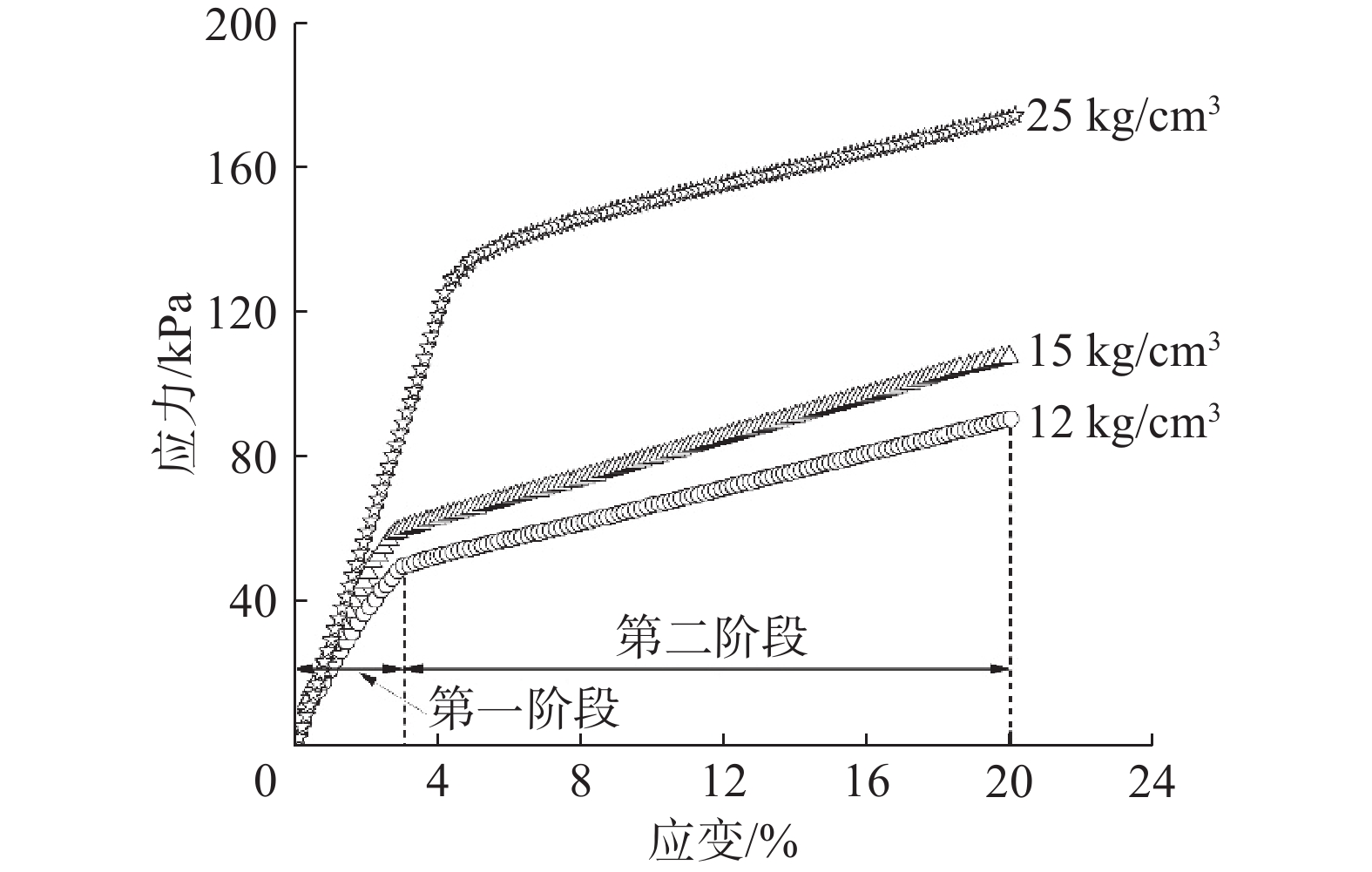
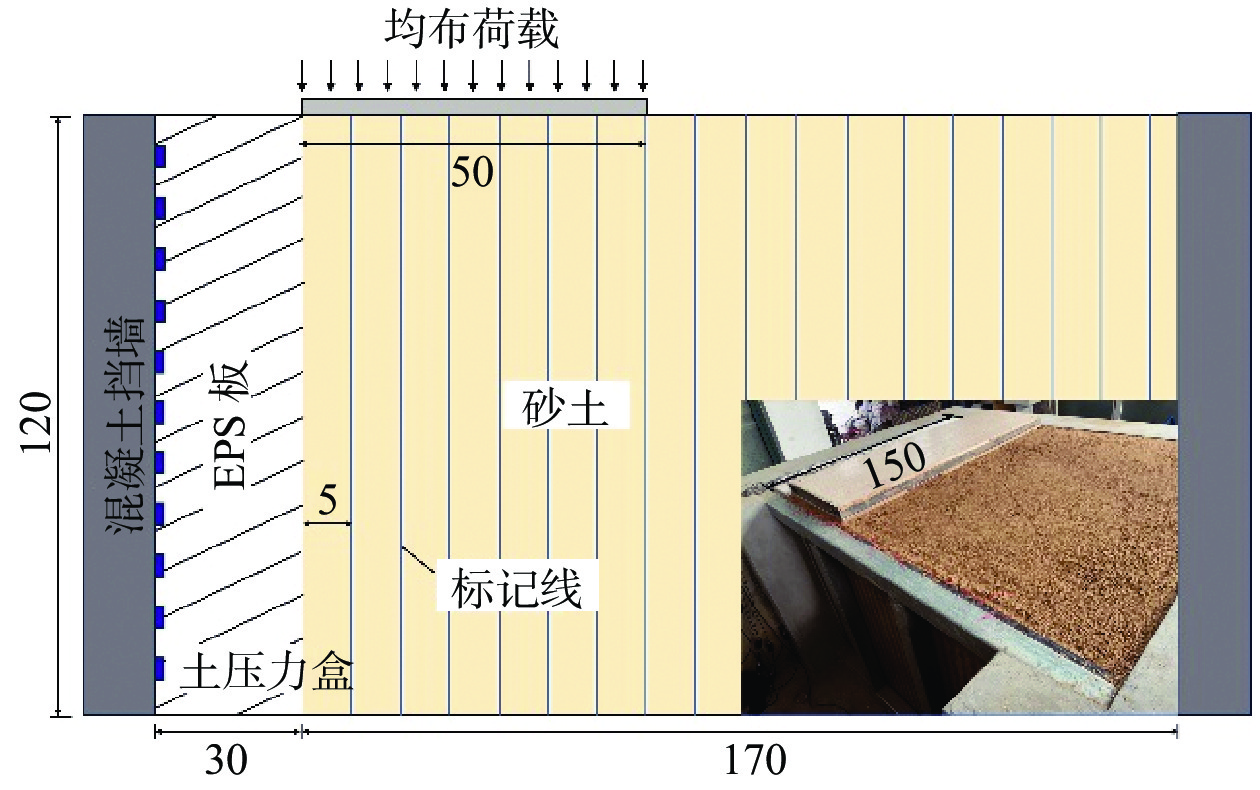
EPS板减压砂土挡墙试验模型由混凝土和有机玻璃围成，尺寸为200.0 cm × 150.0 cm × 120.0 cm（长×宽×高），顶部开放，如图1所示。其中，混凝土挡墙和有机玻璃板的底部及两者衔接处进行固定，以保证其试验过程中保持不动。EPS板紧贴混凝土挡墙墙面放置，EPS板尺寸为30.0 cm × 150.0 cm × 120.0 cm（厚×宽×高），密度为12 kg/m³。取边长为5.0 cm的EPS板立方体块进行压缩试验（压缩速度为10%/min），试验结果如图2所示。可以看出，EPS板压缩应力应变关系曲线近似呈双直线，曲线在两直线交点处应变ε_int约为2.9%，弯点处应力σ_int约为41.6 kPa。

图  1  EPS板减压挡墙模型（单位：cm）

Figure  1.  Model test of a retaining wall with an EPS block (unit: cm)

下载: 全尺寸图片 幻灯片

图  2  EPS板压缩应力应变曲线

Figure  2.  Stress-strain relationship of EPS blocks

下载: 全尺寸图片 幻灯片

EPS板后分层填筑烘干的砂土，所用砂土比重为2.65，砂土填筑压实度为70%（密度为1.73 kg/m³），密度下砂土内摩擦角为33.2°。回填砂土上方放置于50 cm宽的加载板，用于施加上覆荷载。采用有限宽度的上覆荷载而非全宽，是因为荷载宽度过大时，墙底会产生边界效应，影响墙后填土位移形式^[16]。

为了监测EPS板减压砂土挡墙的工作性状，在混凝土挡墙背面每隔0.1 m固定一个直径为2.0 cm、高度为0.5 cm的小型土压力盒（共计11个），如图1所示。土压力盒测量范围为0~50.0 kPa，测量误差小于0.1 kPa。为观察回填砂土的位移模式，在玻璃外侧每隔5.0 cm画数条黑色标记线，玻璃内侧摆列相同数量和位置的红色棉线。内侧的红色棉线可随着回填砂土的移动而移动，通过比较内侧和外侧线条的相对位置获得回填砂土的位移。

1.2   试验结果

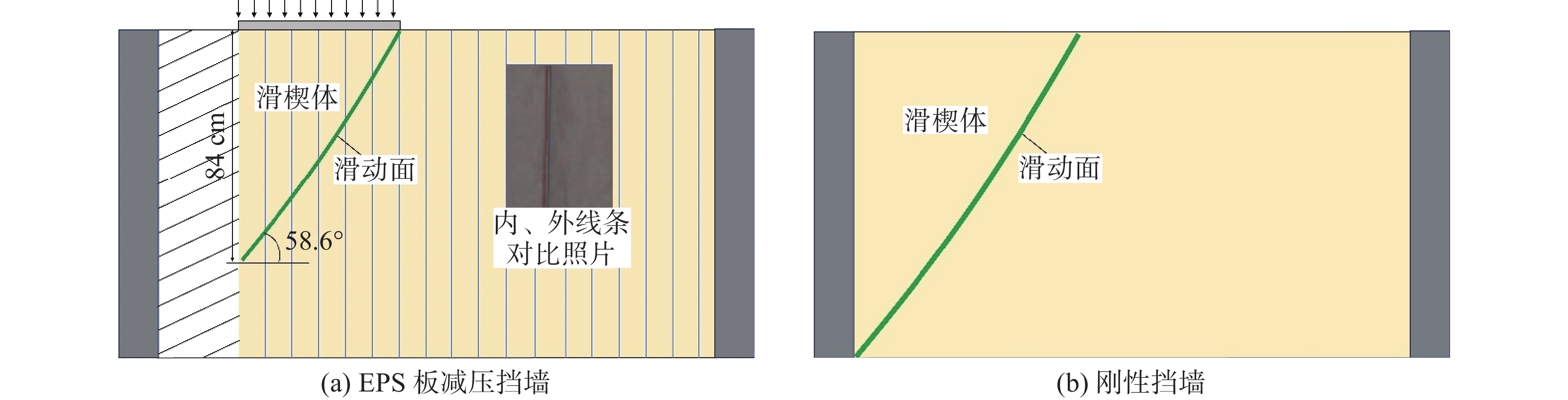
图3（a）为上覆荷载为24.0 kPa时，通过内、外线条比较得到的回填砂土位移。由于EPS板在土压力下的压缩变形，回填砂土中形成滑楔体。滑楔体与刚性挡墙（即没有EPS板等减压措施的混凝土挡墙）墙体背离填土平移时产生的滑楔体的不同之处在于：刚性挡墙墙体刚度较大，墙体在土压力作用下整体发生平移，因此滑楔体穿过墙底^[11]，如图3（b）所示；而在EPS板减压砂土挡墙中，混凝土挡墙固定不动，EPS板是柔性体，因此滑楔体底部可贯穿至EPS板的中部。相同之处在于：滑楔体近似为三角形，EPS板减压砂土挡墙滑楔体滑动角度与刚性挡墙平移引起的滑楔体滑动角度保持一致，均接近库伦滑动角θ^[16]。θ的计算公式为：

图  3  挡墙墙后填土位移模式

Figure  3.  Deformation mode of backfill

下载: 全尺寸图片 幻灯片

式中：$\varphi _{\text{f}} $为填土内摩擦角；δ_f为EPS板与填土的摩擦角。

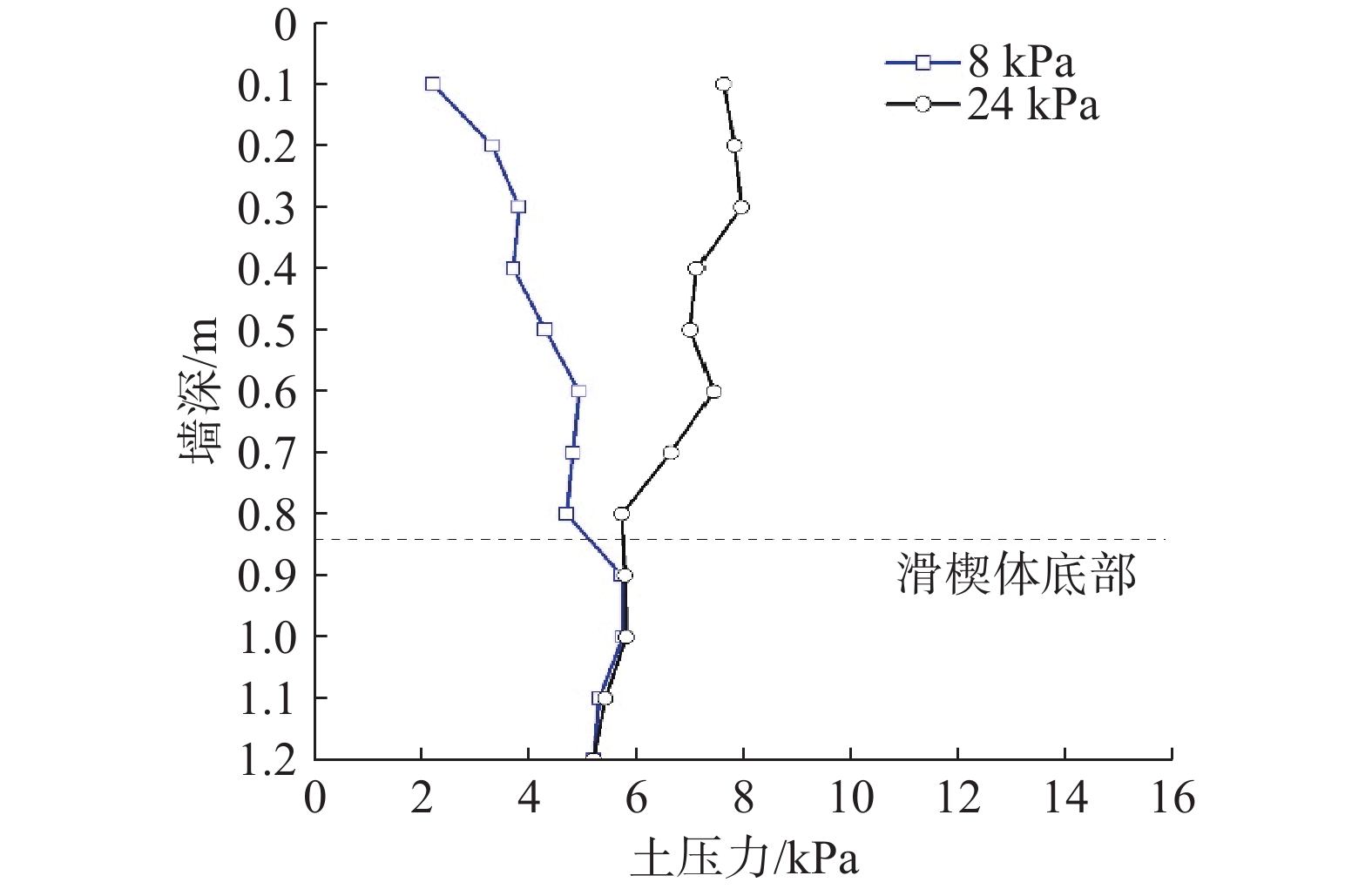
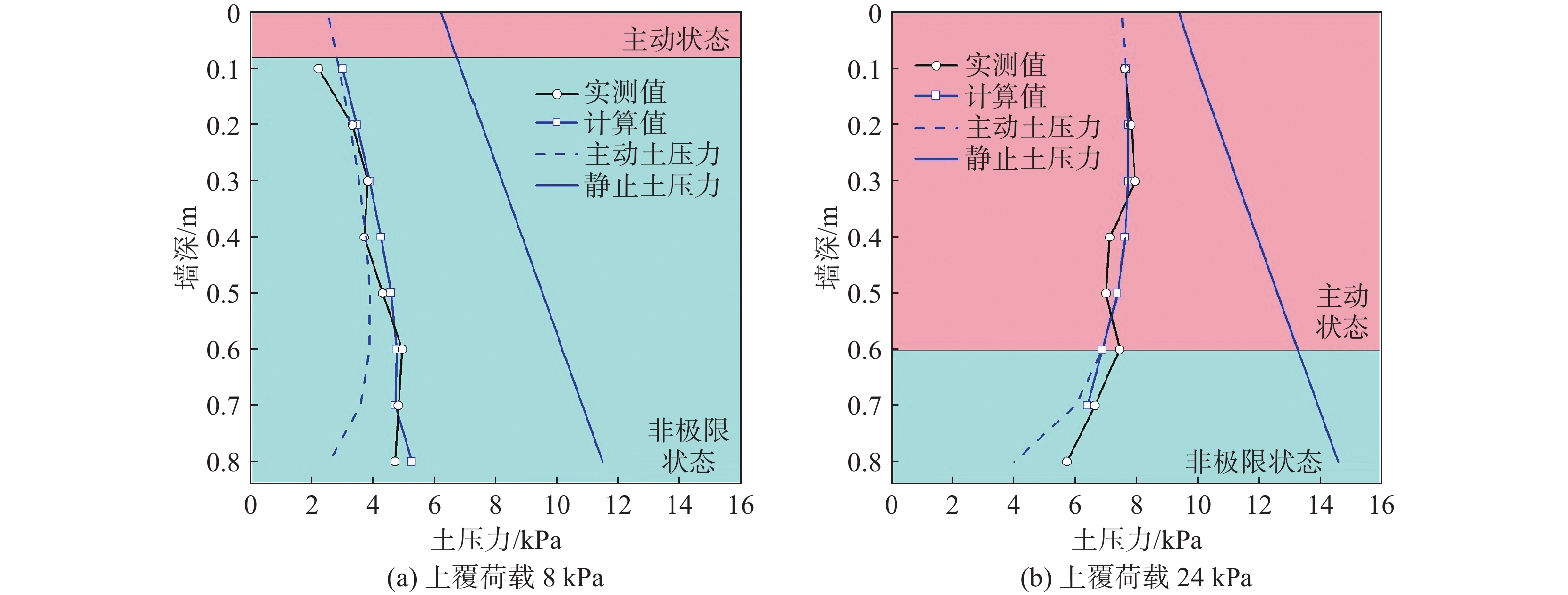
图4为上覆荷载为8.0 和24.0 kPa时，挡墙墙后土压力沿墙深的分布。可以看出，两种上覆荷载作用下EPS板减压砂土挡墙土压力沿墙深均呈现非线性分布。在上覆荷载为8.0 kPa时，土压力随着墙体深度增加而增大；当上覆荷载达到24.0 kPa时，土压力随着墙体深度增加而减小。王元战等^[17]提出，由于上覆荷载作用的影响，挡墙的侧向土压力系数随着深度的增加而减小。因此，在回填土上方施加较大的上覆荷载后，墙顶部的土压力可能会超过底部的土压力。从图4还可以看出，滑楔体下方墙体所受土压力在很大程度上不受上覆荷载的影响，这种情况可能归因于土拱效应，即滑楔体作用力主要作用于左右两侧的EPS板和静止土体，而不是施加给基底填土。

图  4  土压力沿墙深的分布

Figure  4.  Distribution of lateral earth pressure along wall depth

下载: 全尺寸图片 幻灯片

2.   考虑土拱效应的土压力计算方法

2.1   分析模型

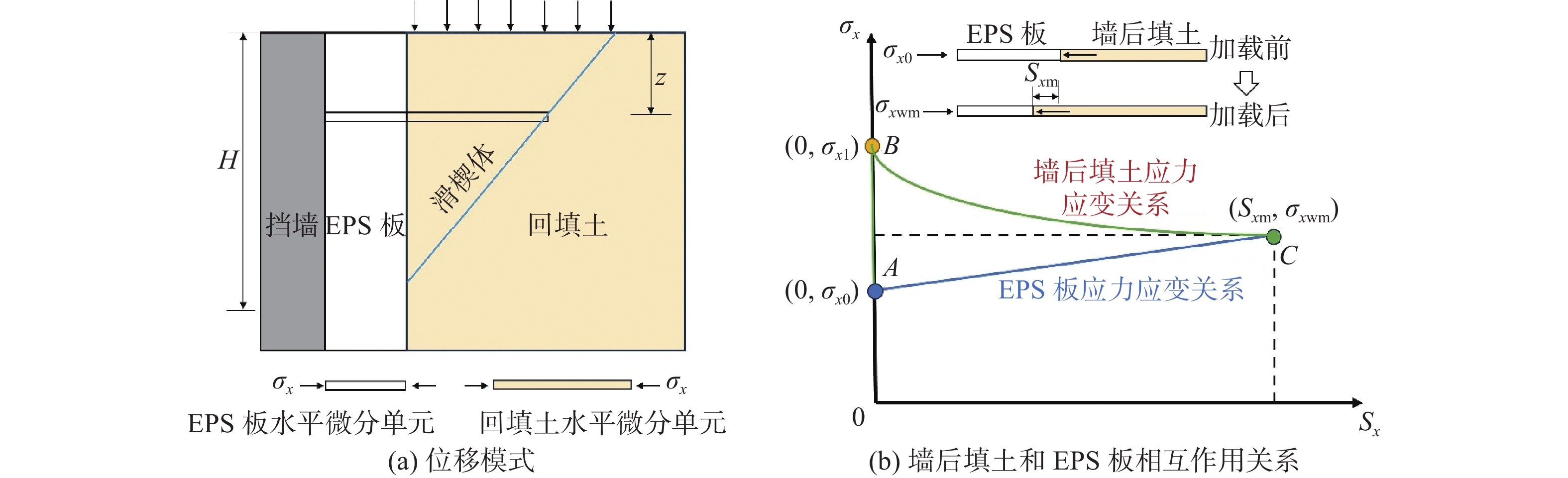
在计算砂性回填土挡墙墙后土压力时，通常以墙后滑楔体为研究对象进行分析。将EPS板和墙后滑楔体分成多个单独存在的水平微分单元，如图5（a）所示。在未施加上覆荷载时，填土和EPS板处于静止状态，此时土压力为静止土压力，深度z处填土水平微分单元产生的水平应力为σ_x0，即图5（b）中的A点状态；在上覆荷载σ_v加载瞬间，填土单元来不及变形，此时填土单元产生的水平应力迅速增大至σ_x1（图5（b）中B点状态）；之后EPS板单元在σ_x1作用下发生压缩变形而填土发生膨胀变形，作用在EPS板单元上的水平应力逐渐增大，填土单元产生的水平应力逐渐减少；当EPS板和填土单元水平位移S_xm和水平应力σ_xwm相等时，即图5（b）中的C点状态，EPS板和填土单元达到平衡状态，两者不再发生变形。达到平衡状态时，EPS板和填土接触面方向并不完全竖直，而是和竖直方向产生一个微小的角度。简化起见，假定EPS板和填土接触面方向完全竖直，则σ_xwm方向完全水平。由于挡墙固定不动，根据力的作用力与反作用力原理，作用在挡墙深度z处的土压力为σ_xwm。

图  5  EPS减压砂土挡墙分析模型

Figure  5.  Analytic model of a retaining wall with an EPS block and sand

下载: 全尺寸图片 幻灯片

2.2   土拱效应

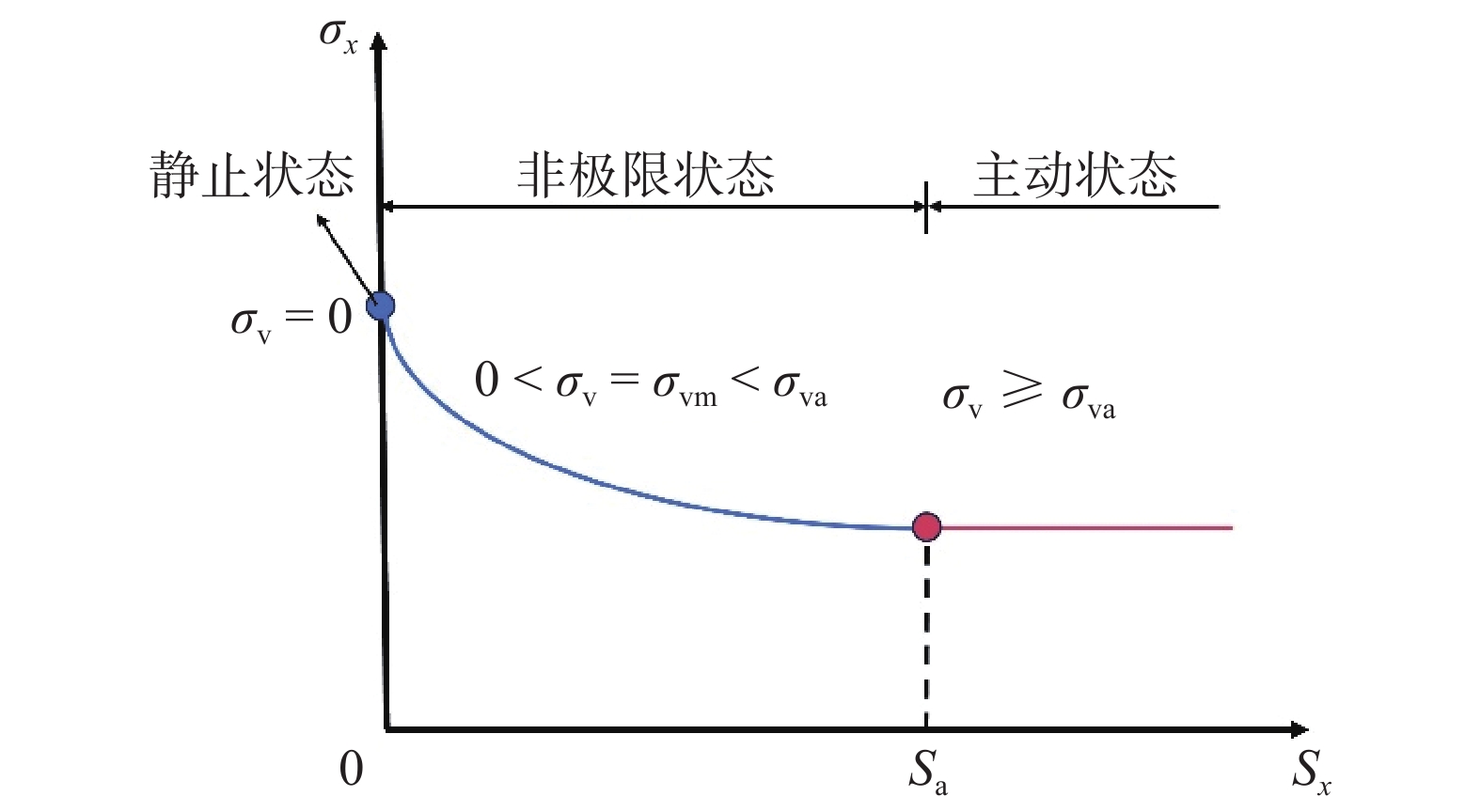
当EPS板侧向压缩位移、应力分别和填土侧向膨胀位移、应力相等时，墙后填土土压力可能处于非极限状态或主动状态。假设上覆荷载增大至σ_va时深度为z处的填土土压力达到主动状态，达到主动状态时填土发生的位移为S_a，那么当上覆荷载σ_v≥σ_va时，墙后填土土压力均处于主动状态，如图6所示；而当上覆荷载σ_v满足0<σ_v=σ_vm<σ_va时，墙后填土则处于非极限状态。实际上，静止状态和主动状态也可以看作是非极限状态的特殊工况，因此本文选择对非极限状态下EPS板减压挡墙墙后回填土滑楔体进行分析。

图  6  墙后填土土压力状态分析

Figure  6.  Analysis of the earth pressure state in backfill

下载: 全尺寸图片 幻灯片

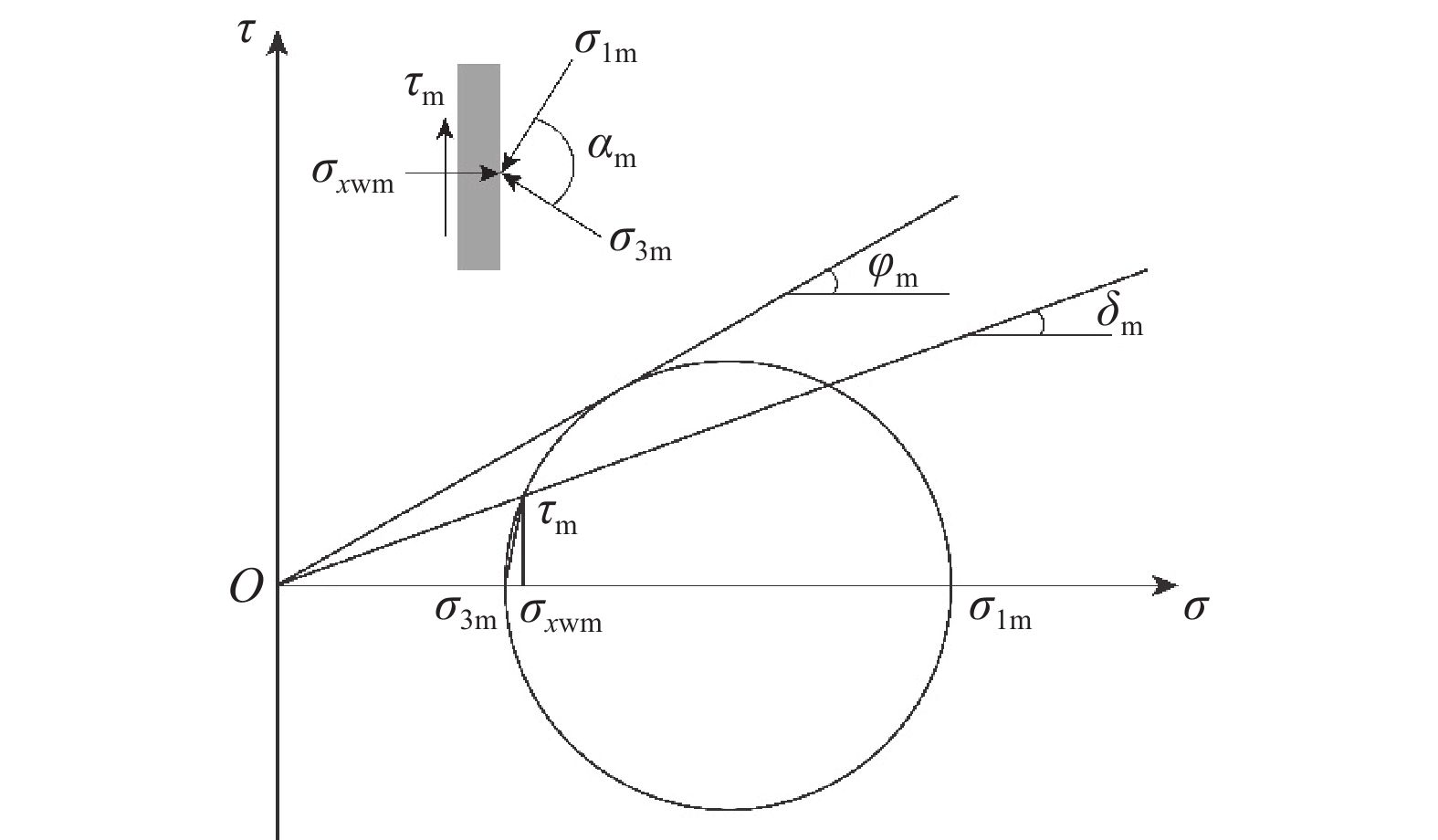
为考虑土拱效应的影响，将滑楔体分成多个单独存在的水平微分单元，如图7所示。深度z处的微分单元宽度B_m=Rcosα_m，其中R为图7所示EPS板背面A点处小主应力土拱线的极径，α_m为A点大主应力方向与水平面的夹角。回填土滑楔体内的土拱形状可假定为圆弧形^[15,18]，由于土拱的影响，图7中最初位于微分单元的点B随后位于凹拱点C处。点C处水平向压力σ_xm表示为：

图  7  墙后填土土拱效应分析

Figure  7.  Analysis of soil arching in the backfill

下载: 全尺寸图片 幻灯片

式中：σ_1m和σ_3m为点C处的大、小主应力；ψ_m为B点大主应力方向与水平面的夹角。相似地，作用在A点的水平应力σ_xwm表示为：

式（3）左右各除以σ_1m，得到：

式中：N_m为大、小主应力之比；N_m = σ_1m/σ_3m =tan²(45+φ_m/2)；φ_m为填土内摩擦角发挥值（φ₀<φ_m<φ_f，φ₀为填土内摩擦角初始值）。

2.3   土压力计算

如果得到填土和EPS板侧向应力应变关系，则可以根据图5（b）所示的挡墙墙后填土和EPS板相互作用关系求得位移S_xm和侧向应力σ_xwm。下面依次对填土和EPS板应力应变关系进行求解。

2.3.1   填土侧向应力与位移关系

式（3）给出了填土侧向应力σ_xwm与α_m、σ_1m的关系，通过求解α_m和σ_1m，则可以得到填土侧向应力σ_xwm的表达式。首先对α_m进行求解。当EPS板背部和土体摩擦角发挥值δ_m小于土体内摩擦角发挥值φ_m时（一般情况下该条件都会成立），利用图8所示的莫尔圆推导α_m的表达式为：

图  8  EPS板相邻土体的莫尔圆

Figure  8.  Mohr circle for stresses in backfill adjacent to the EPS block

下载: 全尺寸图片 幻灯片

式中：τ_m为图7中A点的剪切应力。将τ_m=σ_xwmtanδ_m代入式（5）可以得到：

将式（3）左右除以σ_3m，并代入到式（6）中可得α_m的求解公式：

进一步对σ_1m进行求解。从图7取出微分单元进行受力分析，单元主要受到顶部垂直应力σ_vm（σ_vm=γz+σ_v，γ为填土重度，σ_v为上覆荷载）、底部垂直应力σ_vm+dσ_vm、EPS板的反作用应力p_m、填土静止部分的反作用应力R_m和微分单元自重应力dW_m（dW_m=(H−z)cotθdz，H为滑楔体的高度）。

微分单元水平、垂直方向受力平衡方程以及微分单元与静止土体接触面中点力矩平衡方程分别为：

忽略二阶微分，式（8）~式（10）可分别化简为：

联立式（11）~式（13）可得：

式（14）中，A=2tanθsinδ_m/[tanθsinδ_m(cosδ_mcot(θ−φ_m)−1)]。

对式（14）微分方程求解，并根据z=0的边界条件可得：

根据式（15），作用在微分单元顶部压力可表示为：

根据式（16）可进一步得到σ_1m和σ_vm的关系：

联合式（15）和式（17），则可得到σ_1m的计算公式：

根据式（7）和（18）可分别求解α_m和σ_1m，但在具体求解前还需要知道EPS板背部和土体摩擦角的发挥值δ_m及土体内摩擦角的发挥值φ_m。Bian等^[19]给出了砂土δ_m和φ_m随墙体位移S_m变化的计算公式：

式中：δ₀=φ_f/2；K₀为静止土压力系数，K₀=sinφ_f−0.16^[20]。

给定一个S_xm，根据式（19）得到δ_m和φ_m，然后代入式（7）和（18）进一步求解出a_m和σ_1m，再代入式（3）即可得到填土产生的侧向应力σ_xwm，由此得到填土侧向应力与位移关系。

2.3.2   EPS板侧向应力与位移关系

工程要求EPS板工作时其应力应变曲线应处于如图2所示的第一阶段^[5]，因此EPS板减压挡墙中其应力与变形的关系可表示为：

式中：E_EPS为图2所示第一阶段的EPS板弹性模量，E_EPS=σ_int/ε_int。给定一个S_xm，则可根据式（22）得到EPS板上的水平应力，由此得到EPS板侧向应力与位移的关系。

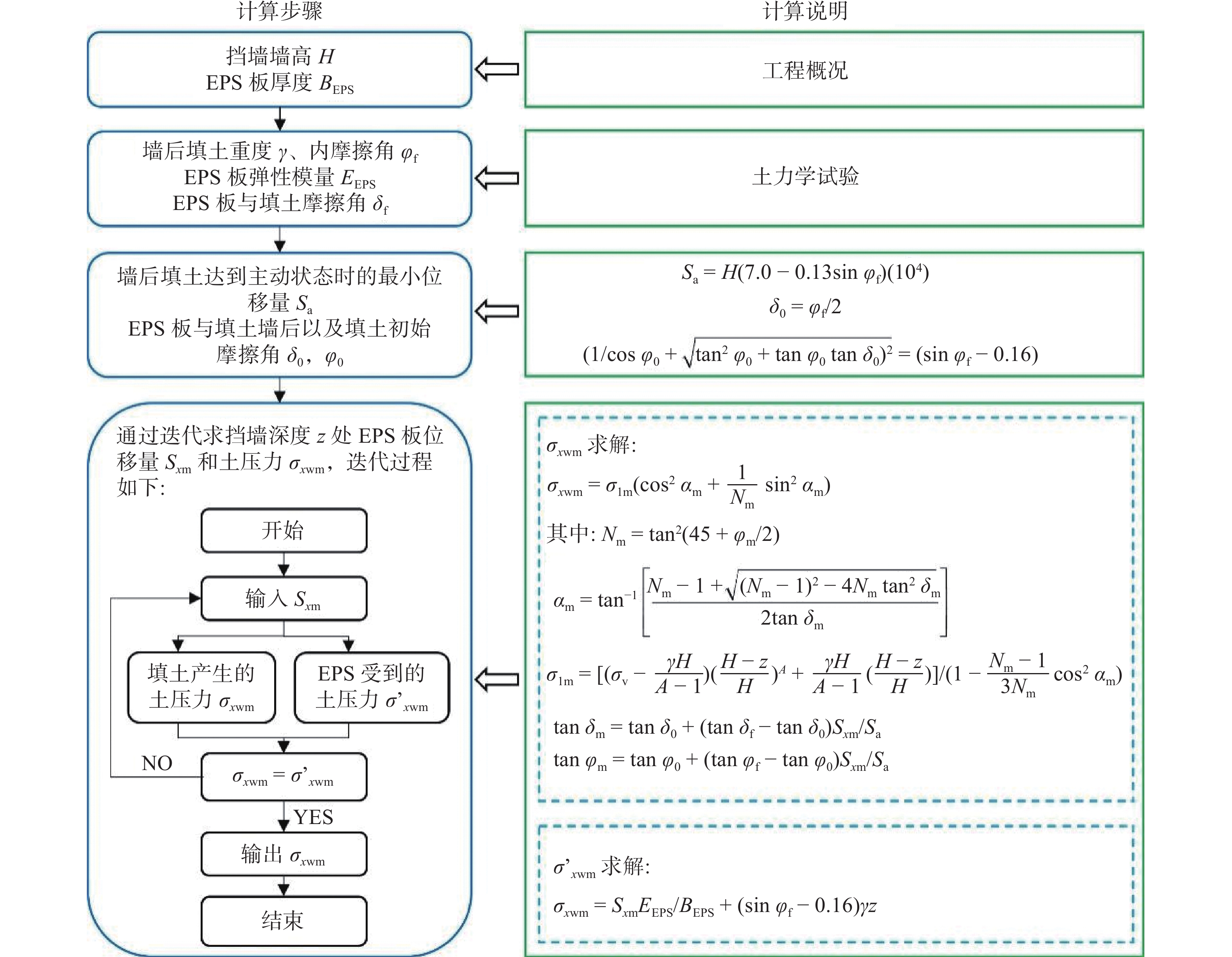
2.4   计算流程

图9给出了本文所提出的EPS板减压砂土挡墙土压力计算方法的具体流程，以便于该方法在工程中的使用。

图  9  EPS板减压砂土挡墙土压力计算流程

Figure  9.  Flowchart for calculating lateral pressure on a retaining wall with an EPS block

下载: 全尺寸图片 幻灯片

3.   案例与影响因素分析

3.1   案例分析

EPS板减压挡墙模型试验中，γ=17.0 kN/m³，φ_f=33.2°，δ_f=19.8°，H=0.84 m，B_EPS=0.30 m，E_EPS=1.435 MPa。根据上述计算方法计算出上覆荷载为8.0和24.0 kPa时EPS板减压挡墙土压力沿墙深的分布如图10所示。可以看出，计算结果与试验结果较为吻合，证明了计算方法的合理性。进一步计算出不同上覆荷载下挡墙静止土压力和主动土压力，如图10所示。从图10（a）可以看出，在8.0 kPa的上覆荷载下，挡墙上部土压力接近主动土压力，表明此部分（粉色部分）回填土处于主动状态，蓝色部分挡墙墙深不同位置的土压力均处于主动与静止土压力之间，这表明此部分墙后回填土处于非极限状态。当上覆荷载达到24.0 kPa时，达到主动状态的填土部分增大。这说明上覆荷载越大，达到主动状态的回填土范围越大。

图  10  不同上覆荷载作用下土压力沿墙深的分布

Figure  10.  Distribution of lateral earth pressure along wall depth under different surcharge loads

下载: 全尺寸图片 幻灯片

3.2   影响因素分析

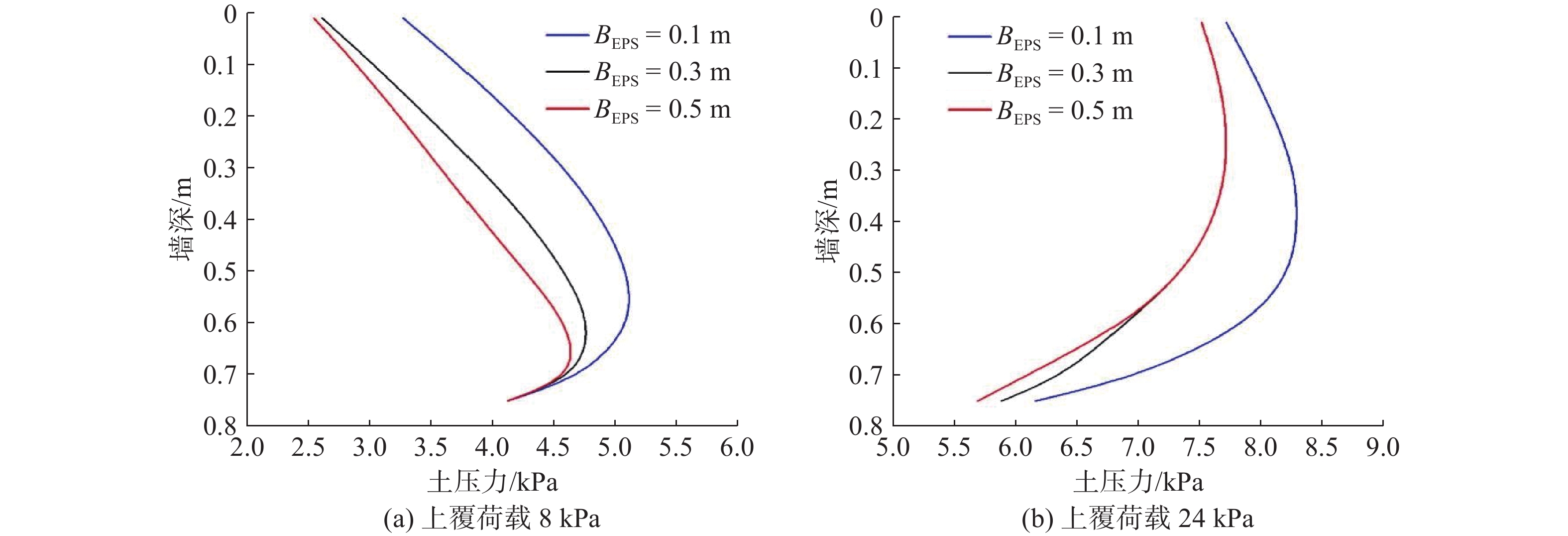
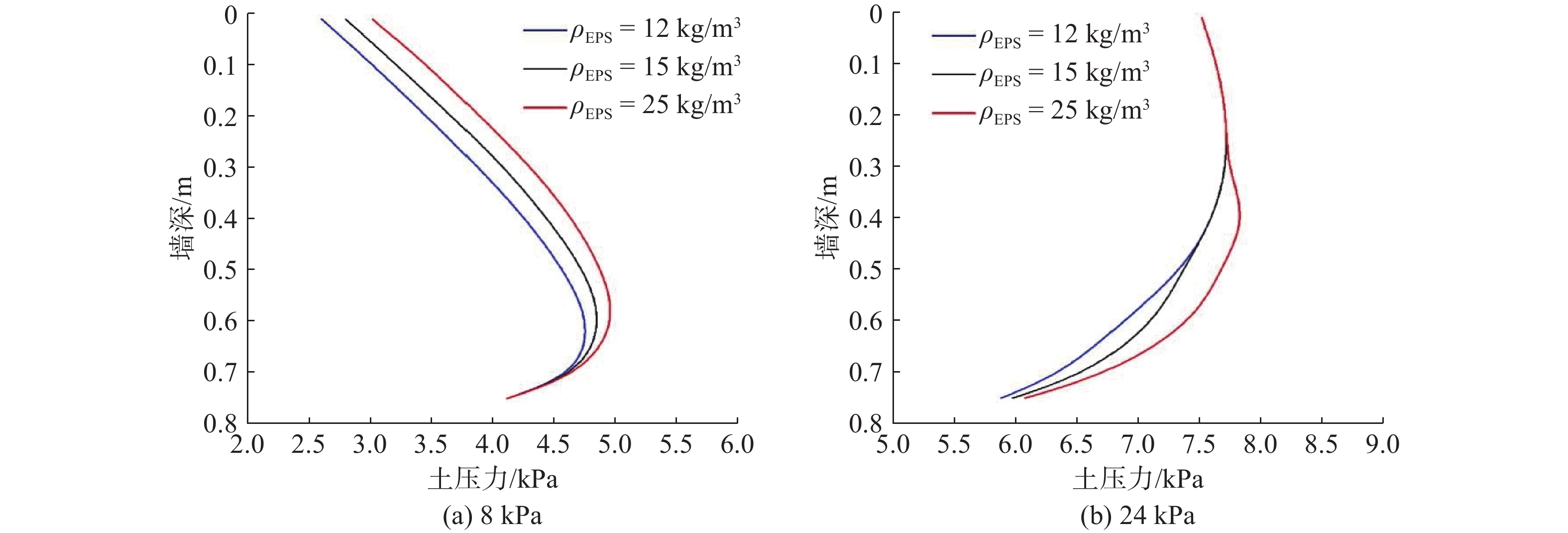
图11给出了EPS板厚度对挡墙土压力分布的影响。随着EPS板厚度的增大，作用在挡墙上的土压力逐渐减少，这是因为在相同荷载下，厚度更大的EPS板位移更大，墙后填土抗剪强度得以更多释放。其中上覆荷载为24.0 kPa时，EPS板厚度从0.30 m增大至0.50 m不同墙深的土压力基本不变。这是因为EPS厚度为0.30 m时，24.0 kPa的上覆荷载下挡墙上部土压力均已达到主动土压力（即最小土压力），即使增大EPS厚度，也只有下部分未达到主动土压力部分的土压力有所减小。

图  11  EPS板厚度对土压力沿墙深分布的影响

Figure  11.  Effect of EPS block thickness on the distribution of lateral earth pressure

下载: 全尺寸图片 幻灯片

分别挑选常见的密度分别为12、15和25 kg/m³的EPS板，探究EPS板密度对土压力分布的影响，3种密度的EPS板压缩应力应变曲线如图2所示。图12给出了不同EPS板密度下挡墙土压力的分布。随着EPS板密度的增大，作用在挡墙上的土压力逐渐增大，这是因为在相同荷载下，密度更大的EPS板弹性模量更大，产生的位移更小。其中上覆荷载为24.0 kPa时，EPS板密度从12 kg/m³增大至25 kg/m³时上部土压力几乎不变。这是因为24.0 kPa的上覆荷载作用下，3种EPS板密度的挡墙上部土压力均为主动土压力。

图  12  EPS板密度对土压力沿墙深分布的影响

Figure  12.  Effect of EPS block density on the distribution of lateral earth pressure

下载: 全尺寸图片 幻灯片

4.   结　语

通过开展EPS板减压砂土挡墙模型试验，研究挡墙墙后回填砂土位移模式和土压力分布规律，在此基础上提出了能够考虑土拱效应的EPS板减压砂土挡墙土压力的计算方法，并分析了EPS板密度和厚度对墙后土压力的影响规律。得到如下主要结论：

（1）上覆荷载作用下EPS板减压砂土挡墙墙后填土中产生近似为三角形的滑楔体，滑楔体滑动角度接近库伦滑动角。与刚性挡墙不同的是，滑楔体并未穿过挡墙底部而是贯穿至土工泡沫中部位置。

（2）上覆荷载作用下EPS板减压砂土挡墙墙后土压力呈非线性分布，随着上覆荷载的增大，土压力和达到主动状态的填土部分也随之增加，其分布规律从随墙深的增加变化为随墙深的减小。

（3）基于微分单元法提出的考虑土拱效应的EPS板减压砂土挡墙土压力计算方法得到的理论结果与试验结果的匹配性较好，证明了计算方法的有效性和适用性。

（4）EPS板厚度越大、密度越小，EPS板对挡墙土压力的减压效果越好；当挡墙土压力变为主动土压力时，EPS板厚度的进一步增大和密度的减少对土压力不再产生影响。

尽管本研究为EPS板减压砂土挡墙设计提供了一定的理论依据，但是当前的研究尚未考虑强震荷载、降雨条件及地下水位变化的影响。这些因素在实际工程应用中可能对挡墙性能产生显著影响，未来应对这些条件下的EPS板性能进行系统研究。