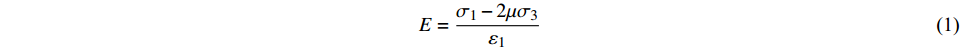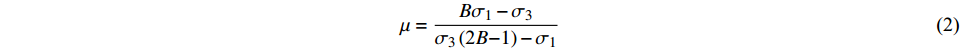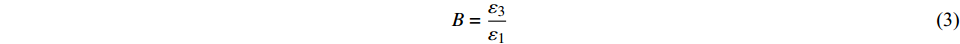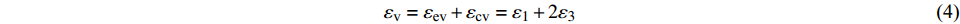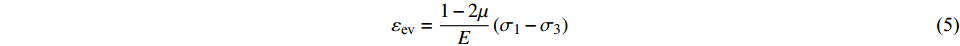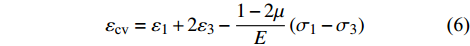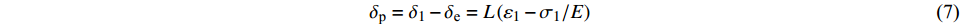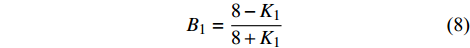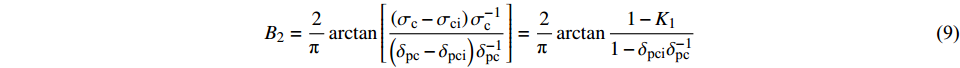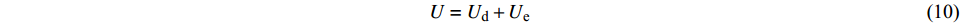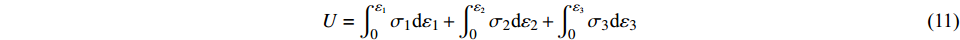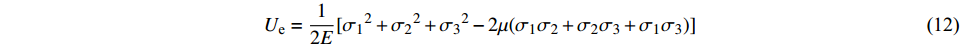Study on mechanical properties and energy evolution of Jinping deep buried marble
-
摘要: 与浅层岩体相比,深层岩体赋存环境更为复杂,导致其力学特性与常见的浅部岩体存在较大差异。锦屏二级隧洞工程最大埋深超过2 500 m,其引水隧洞最高地应力达70 MPa,开展高应力条件下硬岩的力学特性研究,具有重要的理论价值和现实意义。采用四川大学MTS815岩石力学试验系统对取自2 400 m深的锦屏大理岩开展单轴和三轴压缩等系列静态力学试验。试验结果表明:锦屏大理岩的单轴抗压强度为180.43 MPa,随围压的增长,大理岩表现出“脆-延-塑”力学特征,围压32.0 MPa为分界点;同时,起裂应力、损伤应力和峰值应力均具有相似的增长趋势,所定义的脆性指标的下降趋势逐渐趋于平缓;低围压下,弹性能在峰前占主导,而高围压下,耗散能增长更为显著,弹性能峰前峰后差值减小,表现出更为明显的塑性特征。研究结果为准确描述深层岩石力学行为、确保深部工程稳定性提供了一定的理论基础。Abstract: Compared with shallow rock mass, the occurrence environment of deep rock mass is more complex, which leads to the great difference between theri mechanical properties. The maximum buried depth of the tunnel in Jinping II hydropower station is more than 2 500 m, and the maximum ground stress of diversion tunnel is 70 MPa. It is of great theoretical value and practical significance to study the mechanical properties of hard rock under high stress conditions. Therefore, a series of static mechanical tests, including uniaxial and triaxial compression tests, were carried out systematically on Jinping marble from 2 400 m depth by MTS815 rock mechanics test system of Sichuan University. The test results show that the uniaxial compressive strength of Jinping marble is 180.43 MPa. With the increase of confining pressure, the marble shows the mechanical characteristics of “brittle-ductile-plastic” transformation, and 32.0 MPa is a demarcation point. At the same time, there are similar growth trends between the crack initiation stress, crack damage stress and crack peak stress, and the decreasing trend of the brittleness index is gradually flattened. Under low confining pressure, the elastic energy is dominant before the peak, while under high confining pressure, the dissipative energy increases more significantly, and the difference between pre-peak and post-peak elastic energy decreases, showing more obvious plastic characteristics. The research results provide a theoretical basis for accurately describing the mechanical behavior of deep rock and ensuring the stability of deep engineering.
-
随着浅部可开发资源和空间日益减少,地下工程逐渐向更深部发展。我国的矿产开采将主要集中在千米以深的深部岩层,部分水电站的隧洞工程覆盖层已超过2 000 m[1]。开发深度逐渐加深,围岩应力不断增大,导致深埋硬岩隧道工程灾害频发,给深部工程的施工和运营带来巨大挑战。因此,开展高应力条件下硬岩的强度特征和脆性破坏过程等力学特性的研究,具有重要的理论价值和现实意义。
研究表明,随着埋深的加大,强度更大的岩石占比提高,同时破坏机理也随之转化[2]。深部工程岩体由于所处的“三高一扰”环境[3],其力学性质与浅部岩体存在显著差异,表现出明显的非线性特征。为掌握深部岩石的破坏机制,国内外学者进行了大量的试验研究和理论分析。Lau等[4]对Lac du Bonnet花岗岩进行数次室内和原位试验,极大地推动了深部脆性岩石的长期强度、起裂应力、破裂特性等方面研究。不同赋存深度岩石力学行为的差异性主要体现在岩石变形、强度特征和破坏特征等方面。Wagner[5]认为深部岩体的破坏更多表现为岩爆或冲击地压等动态突发性破坏;随赋存深度的增加,李俊如等[6-7]发现岩石的密度、抗拉强度、抗剪强度、单轴抗压强度、弹性模量等力学参数均有逐渐增大的趋势,而吸水率、泊松比则减小;通过三轴压缩试验,Wawersik等[8]揭示了大理岩随围压增长表现出“脆-延-塑”的转换特征;基于单轴、三轴压缩试验,彭俊等[9-10]总结了确定裂纹闭合应力、起裂应力和损伤应力的不同方法,李存宝等[11]研究了不同层理、倾角、围压下页岩的起裂机制并预测出裂纹的平均长度;Zhang等[12-14]提出了考虑不同赋存深度煤岩原位应力环境与物性的双因素模拟试验方法,并系统探索了不同赋存深度煤岩的力学行为、变形破坏特征、损伤和声发射能量的时空演化规律。
锦屏二级水电站工程位于四川省凉山彝族自治州境内,是雅砻江上规模最大的水电站,其隧洞工程由4条引水隧洞、1条排水洞和2条辅助洞(分别称A洞和B洞)组成,一般埋深为1 500~2 000 m,最大埋深达到2 525 m。隧洞沿线80%为大理岩地层,其中,埋深大于1 900 m的白山组大理岩长度约为8 150 m,岩体厚重,完整性高,岩质新鲜[15]。自重和构造作用使隧洞围岩长期处于高地应力环境下,但目前的研究大多针对埋深较浅的岩石材料,对高围压及高应力下深部岩石的静态力学行为研究涉及甚少。
本文以2 400 m埋深的锦屏大理岩为研究对象,主要采用模拟不同深度围压环境的单轴和三轴压缩试验系统分析深埋锦屏大理岩的静态力学特性,并探讨不同围压下锦屏大理岩特征力学参数、脆塑性转化机理及能量耗散规律。研究结果可为深部岩土工程安全开发和运行提供参考依据。
1. 试验准备及方案
试验岩芯取自锦屏二级水电站辅助隧洞埋深2 400 m处,为白山组细晶大理岩,呈灰白色厚层状,密度约2.81 g/cm3。根据《水利水电工程岩石试验规程》(SL 264—2001)[16]的相关规定,单轴、三轴压缩试验采用50 mm×100 mm (Φ×L)的标准圆柱形试件。加工精度满足岩石力学试验要求,并按照“钻孔-岩芯块数字-制取岩样的顺序”进行编号。为尽量减小物理力学性质差别给试验带来的离散性,此次试验所用试件均取自同一钻孔岩芯。
锦屏大理岩静态力学试验选用四川大学MTS Flex Test GT岩石力学试验系统。该系统整体刚度可达10.5 GPa,最大轴向压缩荷载4 600 kN,最大拉伸荷载2 300 kN;轴向位移0~100 mm(±50 mm)。可完成单轴压缩、三轴压缩、直接拉伸、间接拉伸、三点弯曲、纯弯曲等试验项目,满足本次试验要求。
单轴压缩和三轴压缩试验如图1所示,结合锦屏实际地质环境资料[17],锦屏二级水电站上覆岩层平均重度γ = 26.5 kN/m3,对岩样施加σ1=σ3=γH的初始静水压力,开展模拟0、400、800、1 200、1 600、2 000和2 400 m共7种不同深度的锦屏大理岩单轴、三轴压缩力学试验。单轴压缩试验无围压,三轴压缩试验加载至围压设定值,然后控制轴向荷载,加载速率50 kN/min,当荷载升至100 MPa后,转为环向变形控制,初始速率为0.05 mm/min,后将速率升至0.10 mm/min,轴向加压直至大理岩试样破坏。
2. 锦屏大理岩静态力学行为
2.1 锦屏大理岩静态力学特性
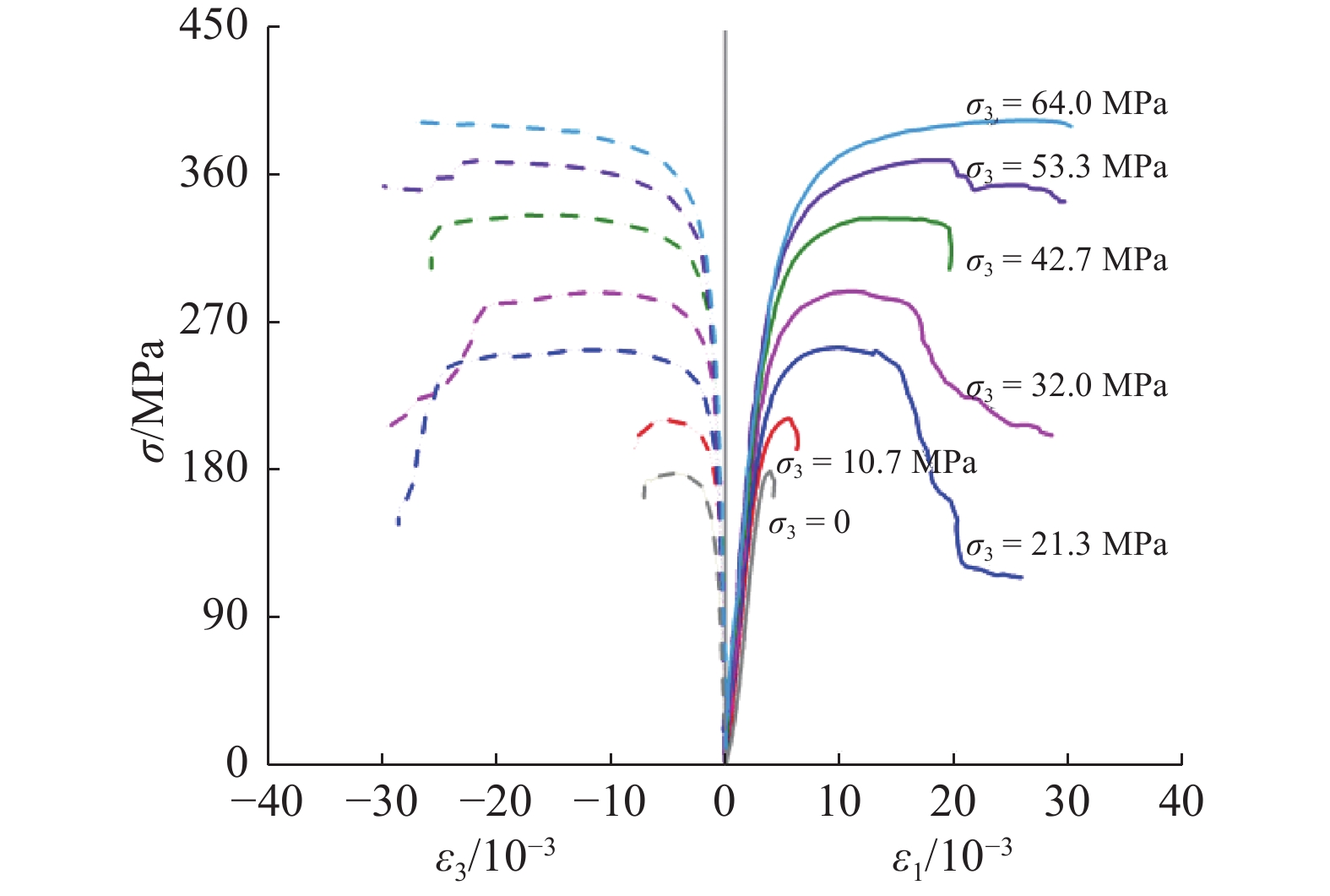
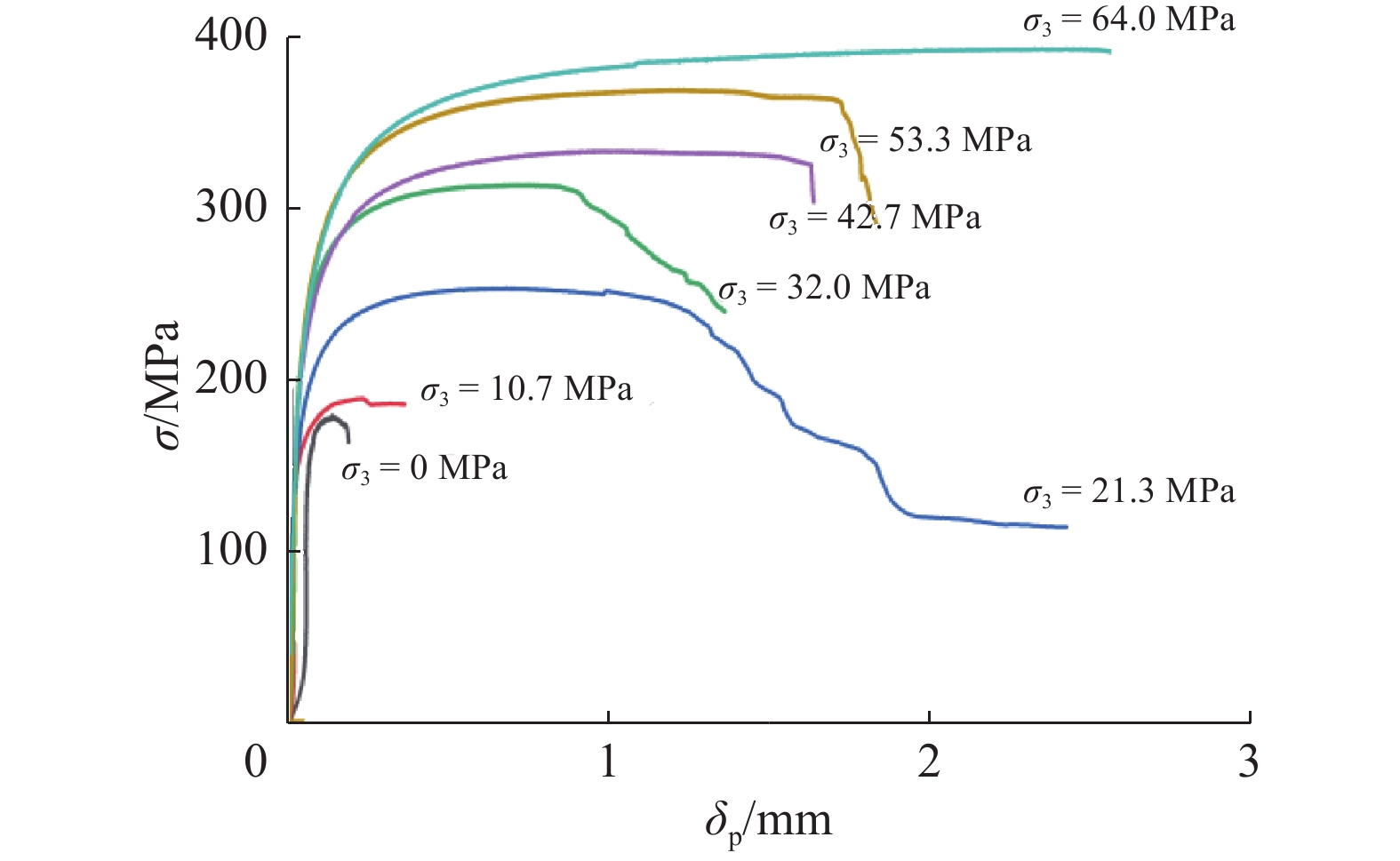
根据单轴和三轴压缩试验采集的数据,得到锦屏大理岩不同模拟深度下的应力应变曲线如图2所示。
由图2可知,单轴和三轴压缩试验条件下,锦屏大理岩均表现出较为明显的弹性-屈服-峰后的变形过程,且围压具有显著影响。随着围压的增加,大理岩的峰值应力呈现逐渐增长的趋势,脆性降低而延性增强,表现出大理岩的脆-延-塑力学特征。当围压超过32.0 MPa后,应力应变曲线达到峰值应力后并不会迅速跌落,出现愈强的“平台”效应,即峰值应力水平基本保持不变的情况下产生一定的应变,随后开始发生跌落,体现出愈强的延性特征;随着围压的增长,塑性特征逐渐明显,到围压64.0 MPa时,在超过3%的轴向应变水平内,岩石的峰值应力降低很少或者基本不降低,峰值应力以后的曲线形态基本表现为理想塑性特性。这表明在高围压条件下,大理岩表现出很强的塑性特性。大理岩出现延塑性转换的围压水平并不高,在10.7~21.3 MPa围压水平即可实现脆-延转换,延-塑转换的围压水平在32.0~42.7 MPa。可见,对于锦屏深埋隧洞的高地应力,围压水平比较容易达到大理岩脆-延-塑转换的量级。
锦屏大理岩的弹性模量E和泊松比μ可通过以下方式计算[16]:
$$ E = \frac{{{\sigma _1} - 2\mu {\sigma _3}}}{{{\varepsilon _1}}} $$ (1) $$ \mu = \frac{{B{\sigma _1} - {\sigma _3}}}{{{\sigma _3}\left( {{\text{2}}B{{ - 1}}} \right)-{\sigma _1}}} $$ (2) $$ B = \frac{{{\varepsilon _3}}}{{{\varepsilon _1}}} $$ (3) 式中:σ1为施加在试件上的轴向应力;σ3为施加在试件上的侧向应力 (单轴试验取σ3 = 0);ε1为测得的轴向应变;ε3为测得的侧向应变。
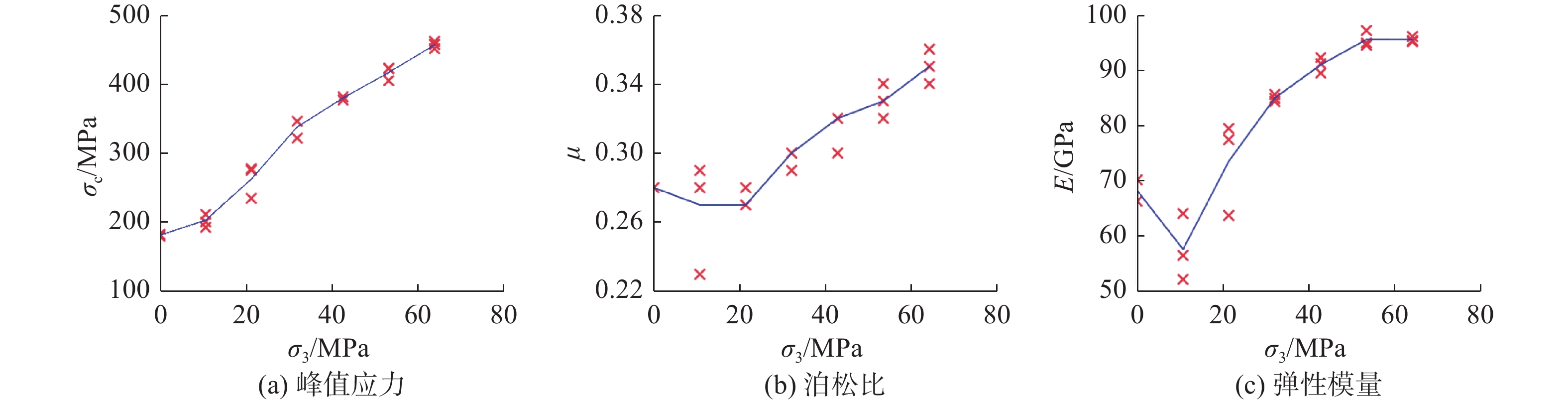
锦屏大理岩特征力学参数与围压的关系如图3所示。可以看出,随着围压的增加,峰值强度σc呈近线性增长趋势,且增长速率在围压为32.0 MPa时存在明显拐点,以该点为界限,峰值强度增长速度有所降低,也再次印证了以该围压为分界点,大理岩的脆性特征减弱、延性特征增强;大理岩泊松比范围为0.27~0.35,随着围压的增加,呈稳定增长趋势;大理岩弹性模量范围为57.69~95.86 GPa,随着围压的增加,大理岩弹性模量呈逐渐增大并最终趋于稳定。
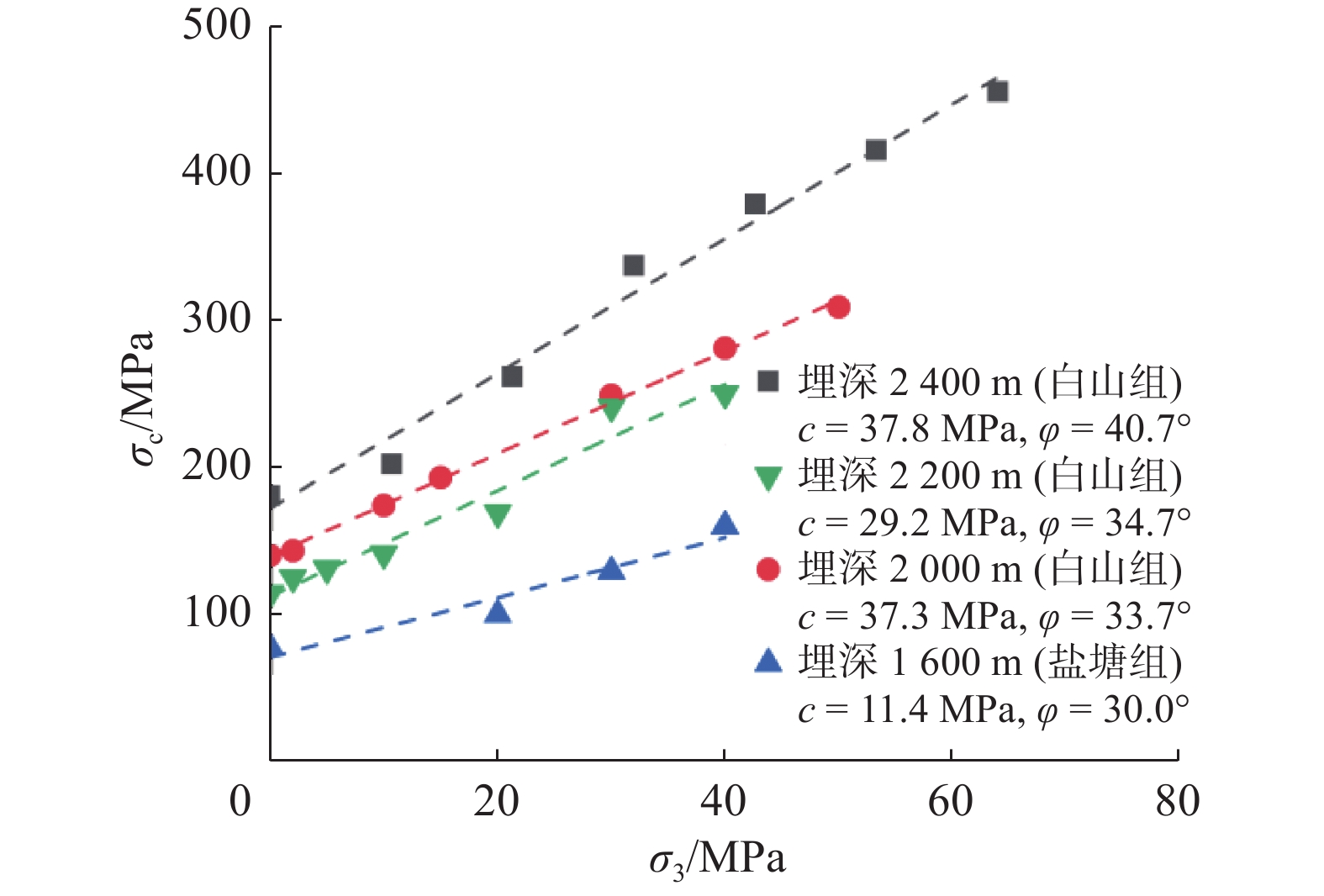
锦屏大理岩的平均单轴抗压强度为180.43 MPa,远高于前人[18]研究的锦屏白山组大理岩平均单轴抗压强度100 MPa。图4为本文和前人[19-21]针对锦屏二级水电站隧道工程区不同埋深大理岩的三轴压缩试验结果。可以看出:随着围压的增长,取自2 400 m埋深的锦屏大理岩强度增长趋势更加明显,并高于平均值,其黏聚力c为37.8 MPa,内摩擦角φ为40.7°,体现了锦屏深埋大理岩内部更强的致密性和结构完整性。同时,由于矿物组成的差异性,白山组大理岩较其他地层(盐塘组等)也表现出更为明显的脆性特征和更高的承载能力。
观察单轴压缩试验后的试件发现,试件表面产生了数条非贯通裂纹,无明显断裂痕迹,同时产生少量碎屑,破坏形式主要为劈裂式张拉破坏,其破坏形态如图5所示。三轴压缩试验后,多数试件产生贯通裂纹,形成明显的单一剪切破坏面,并与轴向呈一定夹角,同时剥落出许多岩屑和岩粉,破坏形式呈典型的三轴压剪破坏,其破坏形态如图6所示。
2.2 锦屏大理岩起裂应力和裂纹损伤应力特征
岩石的宏观破坏往往伴随着裂隙的闭合、起裂、扩展和贯通,其力学特性与内部微裂纹的发育情况密切相关。确定岩石的起裂机制首先要明确裂纹萌生、扩展和贯通的应力阀值,即起裂应力和损伤应力。起裂应力和损伤应力的确定主要有两种方法:声发射法及应变方法[11]。岩石的体积变形εv可假设为由弹性体积应变εev和裂纹体积应变εcv组成,即:
$$ {\varepsilon _{\text{v}}} = {\varepsilon _{{\text{ev}}}} + {\varepsilon _{{\text{cv}}}} = {\varepsilon _1} + 2{\varepsilon _3} $$ (4) 根据广义胡克定律,三轴压缩条件下弹性体积应变为:
$$ {\varepsilon _{{\text{ev}}}} = \frac{{1 - 2\mu }}{E}\left( {{\sigma _1} - {\sigma _3}} \right) $$ (5) 可得裂纹体积应变[11]为:
$$ {\varepsilon _{{\text{cv}}}} = {\varepsilon _1} + 2{\varepsilon _3} - \frac{{1 - 2\mu }}{E}\left( {{\sigma _1} - {\sigma _3}} \right) $$ (6) 岩石起裂应力σci是裂纹体积应变曲线由线性转换为非线性的标志点,在应力未达到起裂应力前,岩石处于弹性状态,其弹性体积应变与总体积应变相等,裂纹体积应变曲线为水平;当受到的应力超过起裂应力后,裂纹体积开始膨胀,试验测得的体积应变将大于理论计算的弹性状态体积应变,裂纹体积应变曲线开始偏移。随着应力的增加,岩石体积变形将由压缩转向膨胀,岩石体积应变-轴向应变曲线将会出现拐点,岩石损伤应力σcd是岩石剪胀开始的标志。当岩石中的应力达到或超过损伤应力后,裂纹产生非稳定扩展并开始汇合,因此损伤应力也被看作为长期强度。
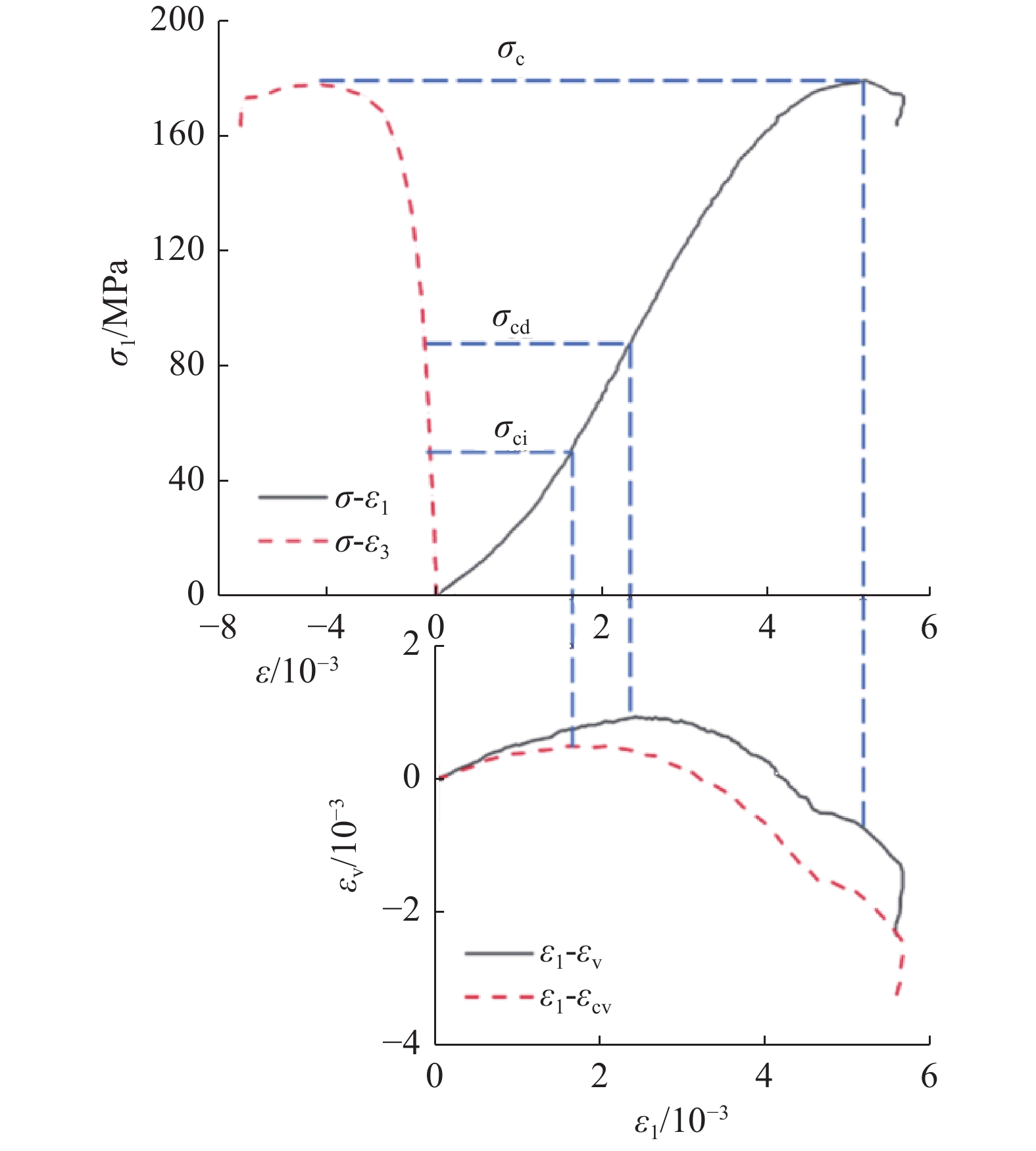
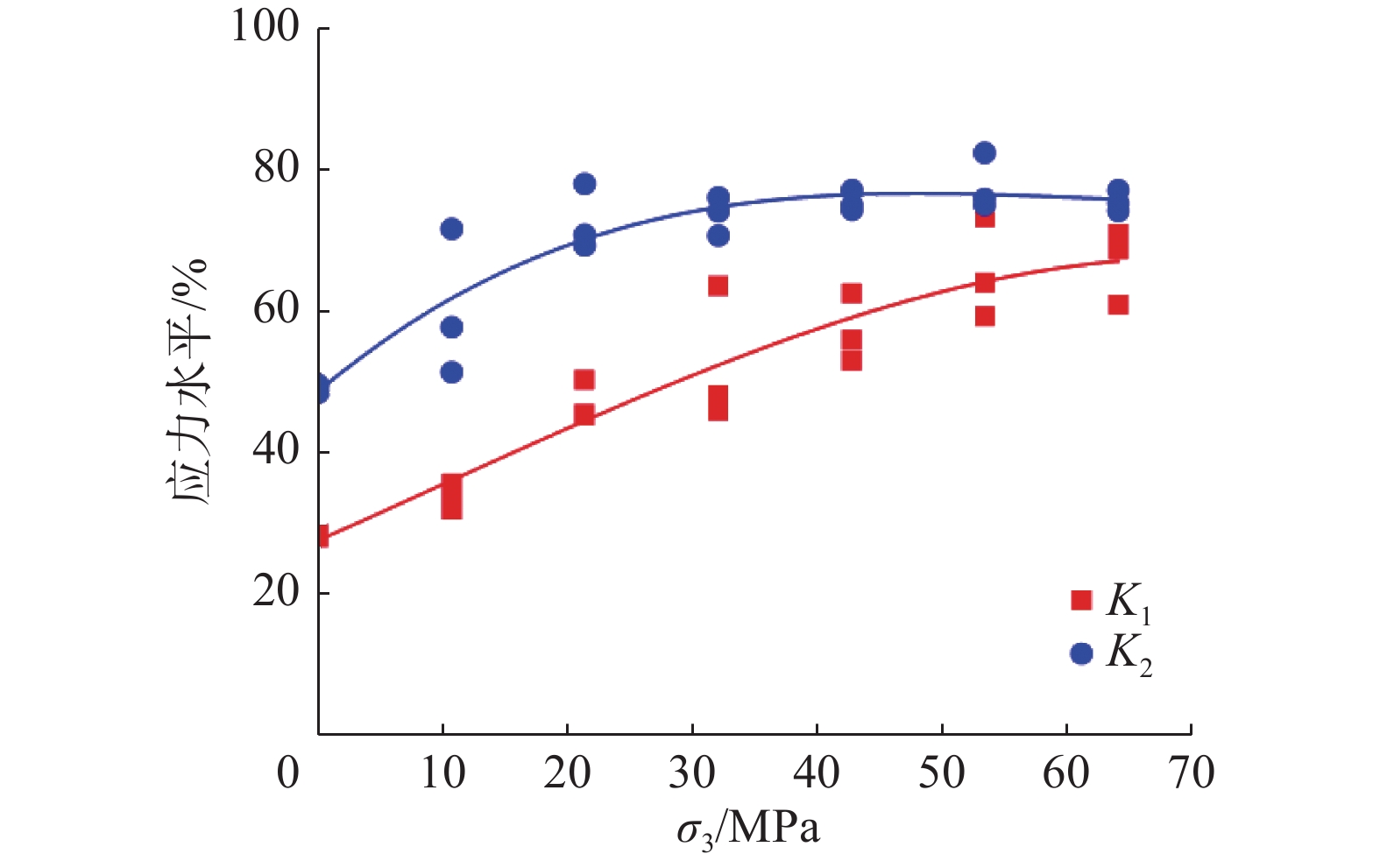
基于锦屏大理岩典型应力应变曲线,其起裂应力和损伤应力的确定如图7所示,根据式(4)和式(6)可分别得到岩石的体积应变和裂纹体积应变,选取裂纹体积应变达到极大值时所对应的应力作为大理岩的起裂应力σci,同理选取岩石体积应变达到极大值时所对应的应力作为大理岩损伤应力σcd,依次对各个围压水平下应力应变数据进行起裂应力和损伤应力的确定,从而获得不同围压下锦屏大理岩的起裂应力和损伤应力(图8);并计算出不同围压条件下大理岩起裂应力水平K1 = σci / σc及损伤应力水平K2 = σcd / σc(图9)。
结合图8可知,随着围压的逐渐增大,岩石峰值应力、损伤应力及起裂应力具有相似的增长趋势,深埋锦屏大理岩起裂应力范围为50.89~305.19 MPa,损伤应力范围为88.62~345.04 MPa,以围压32.0 MPa为拐点,损伤应力的增长速率有所减缓,起裂应力仍近线性增长并逐渐逼近损伤应力。
起裂应力水平K1一定程度上反映了岩石的不均匀性和结构差异,该值越小,岩石的非均质性越强。随着围压的增长,起裂应力水平由28.21%增长到67.01%,这表明围压一定程度上可以弱化岩石力学性能上的不均匀性和差异性,减缓大理岩自身结构缺陷对承载力的影响。损伤应力水平K2一定程度上反映了岩石的长期承载强度。随着围压的增长,损伤应力水平由49.12%增长到75.76%,而在围压32.0 MPa后,损伤应力水平几乎维持不变,这表明在高应力状态下,即高埋深条件下,锦屏大理岩可长时间承受更高荷载的应力状态。一般类结晶岩的损伤应力水平K2为70%~80%[9],与一般类结晶岩石相比,浅埋深条件下锦屏大理岩的损伤应力水平更低。
2.3 锦屏大理岩脆性特征
岩石在压缩过程中,初期主要以弹性变形为主,但随着应力的施加,塑性变形将会逐渐累积。低围压时大理岩屈服破坏,而由围压提供的摩擦力还不能抑制裂隙的滑移,产生塑性变形。随着围压的增大,由围压和轴向应力共同提供正应力,增强了裂隙间的抗滑力,抑制裂隙的滑移。但随着轴压继续增大,大理岩内部裂隙面也会逐步屈服并生成新裂隙,进而引起多个断面相继屈服,塑性变形持续增加,在这一过程中,大理岩的承载能力大致保持恒定,而塑性变形持续增加,即出现了屈服平台。为了更好地描述大理岩的屈服弱化过程,其压缩过程的塑性变形量[22]可表示为:
$$ {\delta _{\text{p}}} = {\delta _1} - {\delta _{\text{e}}} = L\left( {{\varepsilon _1} - {\sigma _1}/E} \right) $$ (7) 式中:L为试件的长度;δ1为轴向变形量;δe为弹性变形量。
锦屏大理岩不同围压下应力-塑性变形量曲线如图10所示。从图10可以发现,低围压下,大理岩的压密阶段具有一定的塑性变形,这是由大理岩内部裂隙闭合引起的,而围压将促进裂纹的闭合,当应力达到一定值后,裂隙就基本闭合。由于去除了压缩过程中大理岩的弹性变形,所以初期其塑性变形量基本相同,近似为0;随着轴压的增长,越逼近峰值强度附近区域内的塑性变形量增长越明显,深埋大理岩塑性变形量更大,即屈服平台相对更长。
岩石脆性指标可以反映岩石脆性特征的差异,通常,岩石脆性指标越大,则该岩石脆性特征越明显。许多学者从应力变化的角度提出了不同的脆性指标,如王宇等[23]基于岩石压拉比及起裂应力水平,将脆性指标定义为:
$$ {B_1} = \frac{{8 - {K_1}}}{{8 + {K_1}}} $$ (8) 但单一从应力角度评价岩石的脆性特征具有一定的局限性。部分学者认为材料的脆性系指材料断裂或破坏前表现出的极小或没有塑性变形的特征[24],从这一角度出发,起裂应力是岩石中裂纹开始生成和扩展的阈值,而后继续加压岩石将产生非弹性变形,至岩石发生屈服变形并破坏。同时,结合图10中的应力-塑性变形量曲线可以发现,起裂应力至峰值应力间的应力与塑性变形关系可以较好描述大理岩的脆塑性转化规律,因此定义脆性指标B2如下:
$$ {B_2} = \frac{2}{{\text{π }}}\arctan \left[ {\frac{{\left( {{\sigma _{\text{c}}} - {\sigma _{{\text{ci}}}}} \right)\sigma _{\text{c}}^{ - 1}}}{{\left( {{\delta _{{\text{pc}}}} - {\delta _{{\text{pci}}}}} \right)\delta _{{\text{pc}}}^{ - 1}}}} \right] = \frac{2}{{\text{π }}}\arctan \frac{{1 - {K_1}}}{{1 - {\delta _{{\text{pci}}}}\delta _{{\text{pc}}}^{ - 1}}} $$ (9) 式中:δpc和δpci分别为峰值应力和起裂应力对应的塑性变形量。在此计算的脆性指标B2取值范围为(0,1),越趋近于1则代表材料的脆性特征越明显,越趋近于0则代表材料的塑性特征越明显。
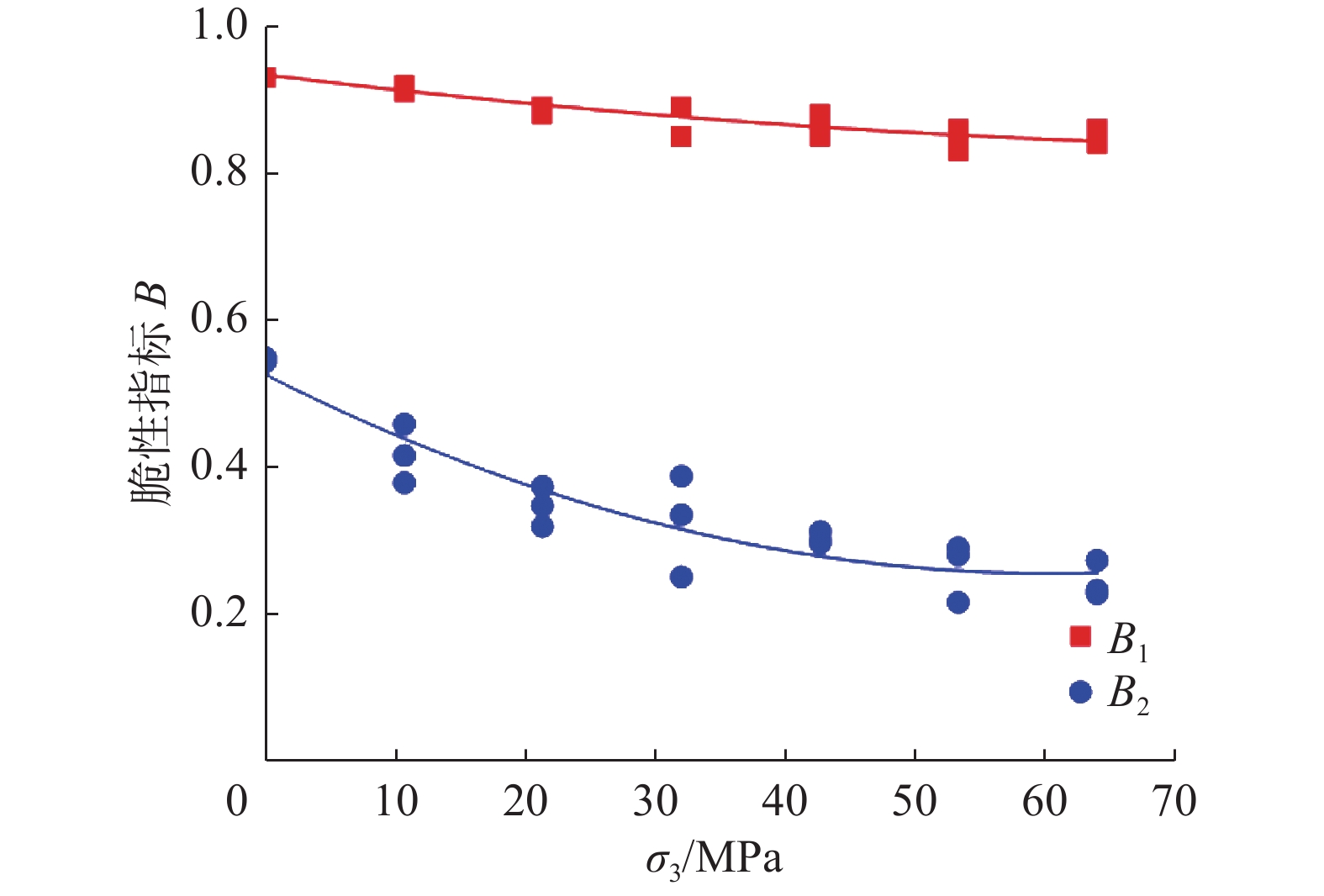
根据式(8)和式(9)分别计算得到图11。可以发现,随着围压的增长,脆性指标B1和B2均呈下降趋势。对比来看,脆性指标B1随围压增长呈近线性下降,无法良好地描述锦屏大理岩的脆塑性转化过程。而脆性指标B2则表现出低围压下变化幅度明显、高围压下逐渐趋于平缓的特征,这表明较低围压浅埋深下锦屏大理岩脆塑性即开始转变,且转变幅度较大。以围压32.0 MPa为临界点,随着埋深和围压的增长,大理岩脆性逐步缓慢减小,而延塑性逐渐增强,大理岩将逐渐到达理想塑性状态。这种随围压的非线性脆性变化特征与前文力学特性相符。
3. 锦屏大理岩能量转化分析
能量转化是物质物理过程的本质,物质破坏是能量驱动下的一种状态失稳现象。岩石在受载破坏时伴随着能量的输入、积聚、耗散和释放,以及不断的能量转移和转化[14]。忽略过程中系统与外界的热交换,根据能量守恒定律有:
$$ U = {U_{\text{d}}} + {U_{\text{e}}} $$ (10) 在主应力空间中,岩体各部分能量[14]表示为:
$$ U = \int_0^{{\varepsilon _1}} {{\sigma _1}{\text{d}}{\varepsilon _1}} + \int_0^{{\varepsilon _2}} {{\sigma _2}{\text{d}}{\varepsilon _2}} + \int_0^{{\varepsilon _3}} {{\sigma _3}{\text{d}}{\varepsilon _3}} $$ (11) $$ {U_{\text{e}}} = \frac{1}{{2E}}[{\sigma _1}^2 + {\sigma _2}^2 + {\sigma _3}^2 - 2\mu ({\sigma _1}{\sigma _2} + {\sigma _2}{\sigma _3} + {\sigma _1}{\sigma _3})] $$ (12) 式中:U为外界输入的能量,即外力对岩石所做的功;Ue为岩石内积聚的弹性能,在满足一定条件下可逆;Ud为岩石变形破坏过程中所耗散的能量,主要导致岩石体的内部损伤,且单向不可逆。
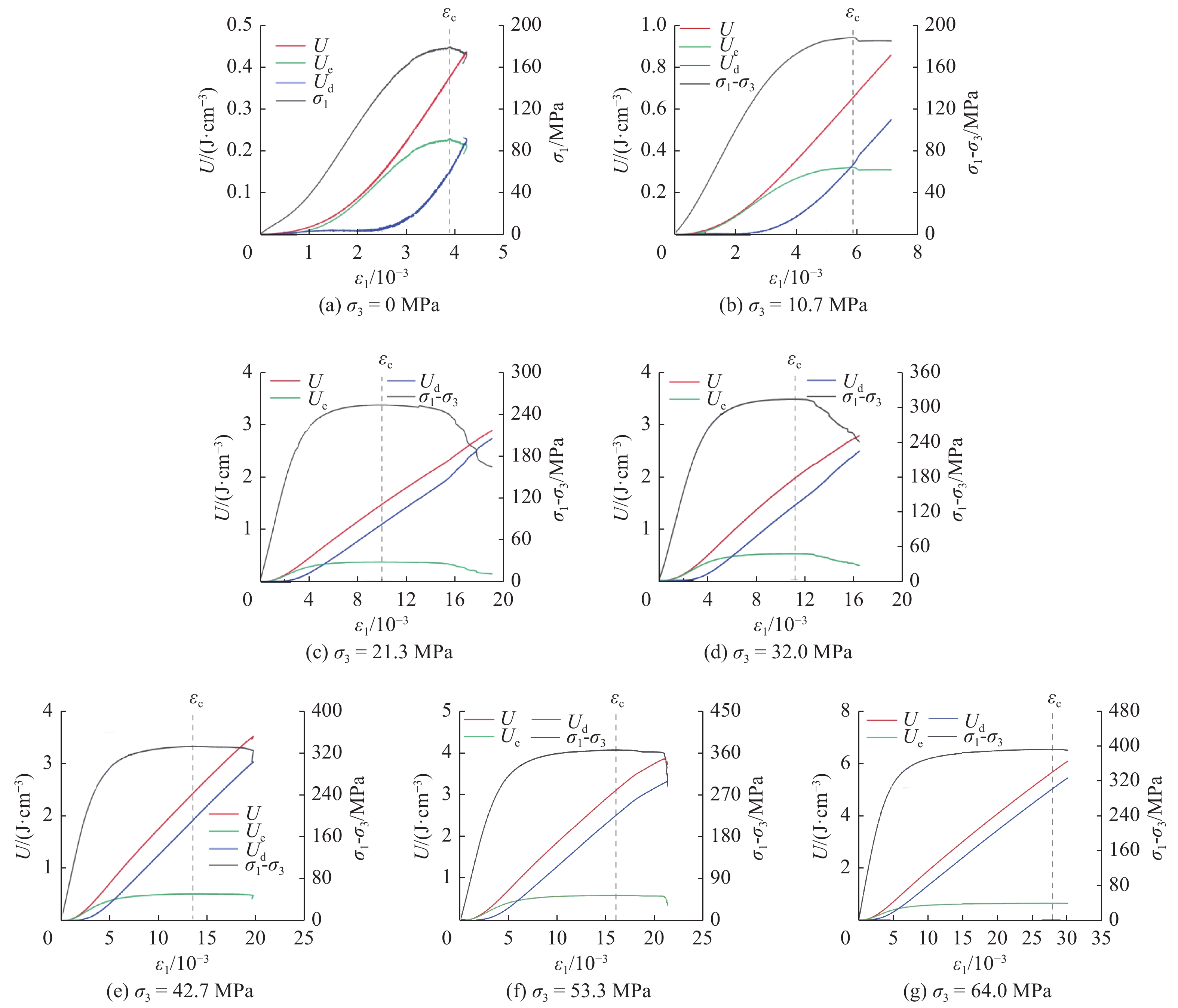
基于单轴和三轴压缩试验数据,计算并绘制U、Ue、Ud随主应变变化的关系(图12),εc表示峰值应力时的应变。
峰前阶段,不同赋存深度锦屏大理岩累计输入能量、积聚弹性能、耗散能均随轴向应变的增加而逐渐增加。整个变形过程中外界将机械能不断输入给大理岩,大理岩一方面将其聚积起来,另一方面耗散能引起自身结构的改变。低围压下,积聚弹性能的增长远远大于耗散能的增长,这表明在峰前阶段大理岩的能量演化行为主要体现为能量积聚,且弹性能增长速率先慢后快;在加载初始的压密阶段增长缓慢,这是由于大理岩初始孔裂隙被压密,大理岩原始刚度较小,能量转化效率低。而高围压下,耗散能的增长远远大于弹性能的增长,并随着围压的增加而逐渐明显,弹性能增长速率呈先快后慢再平稳的趋势。弹性能的驱动和耗散能增加引起了强度的丧失,使得大理岩逐步趋于破坏。
临近破坏时,弹性能增长速率变缓而耗散能的增长速率逐渐变大,大理岩结构发生较大改变,内部微裂隙扩展和汇合显著增加。如图13所示,围压越高,偏应力到达峰值点时大理岩累计输入能量、积聚弹性能、耗散能越高,这表明围压的增大提高了大理岩的峰值强度,使得大理岩吸收能量的能力增大。相比于弹性能,耗散能的围压效应更加明显:围压0 MPa时峰值点耗散能仅为弹性能的55%,到围压64.0 MPa时,峰值点耗散能增长至7.13倍弹性能。两者差距越来越大,这表明用于岩样塑性破坏的耗散能逐渐增加,且主要用于岩样材料内部的摩擦滑移,据此可以理解高围压时岩样产生共扼破裂面需要耗散较多的破坏应变能。
峰后阶段,随着大理岩的破坏,低围压下,积聚的弹性能开始逐渐释放而不断减小,产生跌落,耗散能会大幅增加;高围压下,弹性能能量水平维持较长时间不变后开始减小,耗散能继续保持增长速率,大理岩结构继续发生大的改变,内部裂隙扩展汇合进一步加剧,强度逐步丧失,进而发展至残余阶段。
岩石峰前阶段的耗散能及峰后阶段残余的弹性能越小,岩石的脆性程度越强。随着围压的增大,即埋深增大的条件下,锦屏大理岩峰前耗散能占比逐渐增加,而弹性能峰前峰后差值逐渐减小,塑性特征更加明显。
4. 结 语
基于单轴和三轴压缩等静态力学试验,对锦屏二级水电站深埋(2 400 m)大理岩开展了系统的静态力学特性研究,主要结论如下:
(1)锦屏大理岩单轴抗压强度为180.43 MPa,三轴峰值应力范围为202.15~455.45 MPa。随着围压的增加,脆性特征减弱、延性特征增强,表现出明显的“脆-延-塑”力学特征。深埋锦屏大理岩围压效应更加明显,这体现了深埋大理岩内部更强的致密性和结构完整性。
(2)随模拟深度的增加,锦屏大理岩起裂应力和损伤应力表现出与峰值应力相似的增长趋势,起裂应力水平K1由28.21%增长到67.01%,损伤应力水平K2由49.12%增长到75.76%。
(3)基于岩石应力与塑性变形关系,定义了可准确描述锦屏大理岩脆塑转化规律的脆性指标,该脆性指标表现出低围压下下降幅度明显而高围压下逐渐趋于平缓的非线性变化趋势。
(4)锦屏大理岩力学特性随围压变化存在明显分界点(围压32.0 MPa),在该分界点前后峰值应力、损伤应力水平、所定义的脆性指标均有明显变化。这表明锦屏大理岩存在一个特征埋深,该埋深以浅和以深会出现相对显著的力学特性变化。
(5)从能量特征角度,峰值点锦屏大理岩累计输入能量、积聚弹性能、耗散能均随围压的增长而增长,耗散能的增长更为显著。低围压下,弹性能峰后存在跌落;而高围压下,弹性能峰前峰后差值逐渐减小,塑性特征更加明显。
-
-
[1] 周宏伟, 谢和平, 左建平. 深部高地应力下岩石力学行为研究进展[J]. 力学进展,2005,35(1):91-99 doi: 10.6052/1000-0992-2005-1-J2004-018 ZHOU Hongwei, XIE Heping, ZUO Jianping. Developments in researches on mechanical behaviors of rocks under the condition of high ground pressure in the depths[J]. Advances in Mechanics, 2005, 35(1): 91-99. (in Chinese) doi: 10.6052/1000-0992-2005-1-J2004-018
[2] 周维垣. 高等岩石力学[M]. 北京: 水利电力出版社, 1990. ZHOU Weiheng. Advanced rock mechanics[M]. Beijing: Water Resources and Electric Power Press, 1990. (in Chinese)
[3] 何满潮, 谢和平, 彭苏萍, 等. 深部开采岩体力学研究[J]. 岩石力学与工程学报,2005,24(16):2803-2813 doi: 10.3321/j.issn:1000-6915.2005.16.001 HE Manchao, XIE Heping, PENG Suping, et al. Study on rock mechanics in deep mining engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(16): 2803-2813. (in Chinese) doi: 10.3321/j.issn:1000-6915.2005.16.001
[4] LAU J S O, CHANDLER N A. Innovative laboratory testing[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1427-1445. doi: 10.1016/j.ijrmms.2004.09.008
[5] WAGNER H. Support requirements for rockburst conditions[C]∥GAY N C, WAINWRIGHT E H. Proceedings of 1st International Congress on Rockbursts and Seismicity in Mines. Johannesburg: SAIMM, 1984: 209-218.
[6] 李俊如, 李海波. 不同埋深岩石力学特性的实验研究[J]. 岩石力学与工程学报,2001,20(增刊1):948-951 LI Junru, LI Haibo. Experimental study on mechanical properties of rock at different depth[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(Suppl1): 948-951. (in Chinese)
[7] 李鹏波, 王金安. 煤层上覆岩层力学性质随赋存深度变化试验[J]. 哈尔滨工业大学学报,2015,47(12):98-101 doi: 10.11918/j.issn.0367-6234.2015.12.017 LI Pengbo, WANG Jin’an. Experimental on mechanical properties of overlying strata rock changed with the occurrence depth[J]. Journal of Harbin Institute of Technology, 2015, 47(12): 98-101. (in Chinese) doi: 10.11918/j.issn.0367-6234.2015.12.017
[8] WAWERSIK W R, FAIRHURST C. A study of brittle rock fracture in laboratory compression experiments[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1970, 7(5): 561-575.
[9] 彭俊, 蔡明, 荣冠, 等. 裂纹闭合应力及其岩石微裂纹损伤评价[J]. 岩石力学与工程学报,2015,34(6):1091-1100 PENG Jun, CAI Ming, RONG Guan, et al. Stresses for crack closure and its application to assessing stress-induced microcrack damage[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(6): 1091-1100. (in Chinese)
[10] 周辉, 孟凡震, 卢景景, 等. 硬岩裂纹起裂强度和损伤强度取值方法探讨[J]. 岩土力学,2014,35(4):913-918, 925 ZHOU Hui, MENG Fanzhen, LU Jingjing, et al. Discussion on methods for calculating crack initiation strength and crack damage strength for hard rock[J]. Rock and Soil Mechanics, 2014, 35(4): 913-918, 925. (in Chinese)
[11] 李存宝, 谢和平, 谢凌志. 页岩起裂应力和裂纹损伤应力的试验及理论[J]. 煤炭学报,2017,42(4):969-976 LI Cunbao, XIE Heping, XIE Lingzhi. Experimental and theoretical study on the shale crack initiation stress and crack damage stress[J]. Journal of China Coal Society, 2017, 42(4): 969-976. (in Chinese)
[12] ZHANG Z P, XIE H P, ZHANG R, et al. Deformation damage and energy evolution characteristics of coal at different depths[J]. Rock Mechanics and Rock Engineering, 2019, 52(5): 1491-1503. doi: 10.1007/s00603-018-1555-5
[13] JIA Z Q, XIE H P, ZHANG R, et al. Acoustic emission characteristics and damage evolution of coal at different depths under triaxial compression[J]. Rock Mechanics and Rock Engineering, 2020, 53(5): 2063-2076. doi: 10.1007/s00603-019-02042-w
[14] JIA Z Q, LI C B, ZHANG R, et al. Energy evolution of coal at different depths under unloading conditions[J]. Rock Mechanics and Rock Engineering, 2019, 52(11): 4637-4649. doi: 10.1007/s00603-019-01856-y
[15] 刘宁, 张春生, 褚卫江, 等. 深埋大理岩力学特性对岩爆发生条件的影响分析[J]. 岩土力学,2013,34(9):2638-2642, 2648 LIU Ning, ZHANG Chunsheng, CHU Weijiang, et al. Influence of mechanical characteristics of deep-buried marble on rockburst occurrence conditions[J]. Rock and Soil Mechanics, 2013, 34(9): 2638-2642, 2648. (in Chinese)
[16] 中华人共和国水利部. 水利水电工程岩石试验规程: SL 264—2001[S]. 北京: 中国水利水电出版社, 2001. Ministry of Water Resources of the People’s Republic of China. Specifications for rock tests in water conservancy and hydroelectric engineering: SL 264—2001[S]. Beijing: China Water & Power Press, 2001. (in Chinese)
[17] 葛修润, 侯明勋. 钻孔局部壁面应力解除法(BWSRM)的原理及其在锦屏二级水电站工程中的初步应用[J]. 中国科学:技术科学,2012,55(4):939-949 doi: 10.1007/s11431-011-4680-x GE Xiurun, HOU Mingxun. Principle of in-situ 3D rock stress measurement with borehole wall stress relief method and its preliminary applications to determination of in-situ rock stress orientation and magnitude in Jinping hydropower station[J]. Science China Technological Sciences, 2012, 55(4): 939-949. (in Chinese) doi: 10.1007/s11431-011-4680-x
[18] 张传庆, 张玲, 周辉, 等. 深部硬岩的力学特性与支护要求[J]. 武汉工程大学学报,2018,40(5):543-549 doi: 10.3969/j.issn.1674-2869.2018.05.013 ZHANG Chuanqing, ZHANG Ling, ZHOU Hui, et al. Mechanical properties and support requirements of hard rock in deep engineering[J]. Journal of Wuhan Institute of Technology, 2018, 40(5): 543-549. (in Chinese) doi: 10.3969/j.issn.1674-2869.2018.05.013
[19] 张春生, 陈祥荣, 侯靖, 等. 锦屏二级水电站深埋大理岩力学特性研究[J]. 岩石力学与工程学报,2010,29(10):1999-2009 ZHANG Chunsheng, CHEN Xiangrong, HOU Jing, et al. Study of mechanical behavior of deep-buried marble at Jinping Ⅱ hydropower station[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(10): 1999-2009. (in Chinese)
[20] 李宏哲, 夏才初, 闫子舰, 等. 锦屏水电站大理岩在高应力条件下的卸荷力学特性研究[J]. 岩石力学与工程学报,2007,26(10):2104-2109 doi: 10.3321/j.issn:1000-6915.2007.10.021 LI Hongzhe, XIA Caichu, YAN Zijian, et al. Study on marble unloading mechanical properties of Jinping hydropower station under high Geostress conditions[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(10): 2104-2109. (in Chinese) doi: 10.3321/j.issn:1000-6915.2007.10.021
[21] 王建良. 深埋大理岩力学特性研究及其工程应用[D]. 昆明: 昆明理工大学, 2013. WANG Jianliang. Mechanical characteristics of deeply buried marble and its technical application[D]. Kunming: Kunming University of Science and Technology, 2013. (in Chinese)
[22] 苏承东, 张振华. 大理岩三轴压缩的塑性变形与能量特征分析[J]. 岩石力学与工程学报,2008,27(2):273-280 doi: 10.3321/j.issn:1000-6915.2008.02.007 SU Chengdong, ZHANG Zhenhua. Analysis of plastic deformation and energy property of marble under pseudo-triaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(2): 273-280. (in Chinese) doi: 10.3321/j.issn:1000-6915.2008.02.007
[23] 王宇, 李晓, 武艳芳, 等. 脆性岩石起裂应力水平与脆性指标关系探讨[J]. 岩石力学与工程学报,2014,33(2):264-275 WANG Yu, LI Xiao, WU Yanfang, et al. Research on relationship between crack initiation stress level and brittleness indices for brittle rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(2): 264-275. (in Chinese)
[24] HOWELL J V. Glossary of geology and related sciences[M]. Washington: American Geological Institute, 1957: 99-102.
-
期刊类型引用(4)
1. 朱伟豪,董璐,李洪亚,马林建,张思懿. 三轴压缩下白云岩力学特性及能量演化规律. 土工基础. 2024(02): 350-355 .  百度学术
百度学术
2. 祝威,高霞,张保勇,吴强. 不同围压与饱和度下含瓦斯水合物煤体能量变化规律. 煤田地质与勘探. 2024(04): 21-34 .  百度学术
百度学术
3. 王卿,王振清,陈叶青,李春海. 高围压下深部大理岩变形特性与能量演化试验研究. 防护工程. 2023(02): 7-15 .  百度学术
百度学术
4. 任洋,吴云峰. 不同循环加卸载速率下砂岩的力学特性研究. 有色金属工程. 2022(11): 111-119 .  百度学术
百度学术
其他类型引用(7)



 Email Alerts
Email Alerts RSS
RSS

 下载:
下载: