Email Alerts
RSS
Permeability coefficient investigation based on fractal characteristics of porous media soil
-
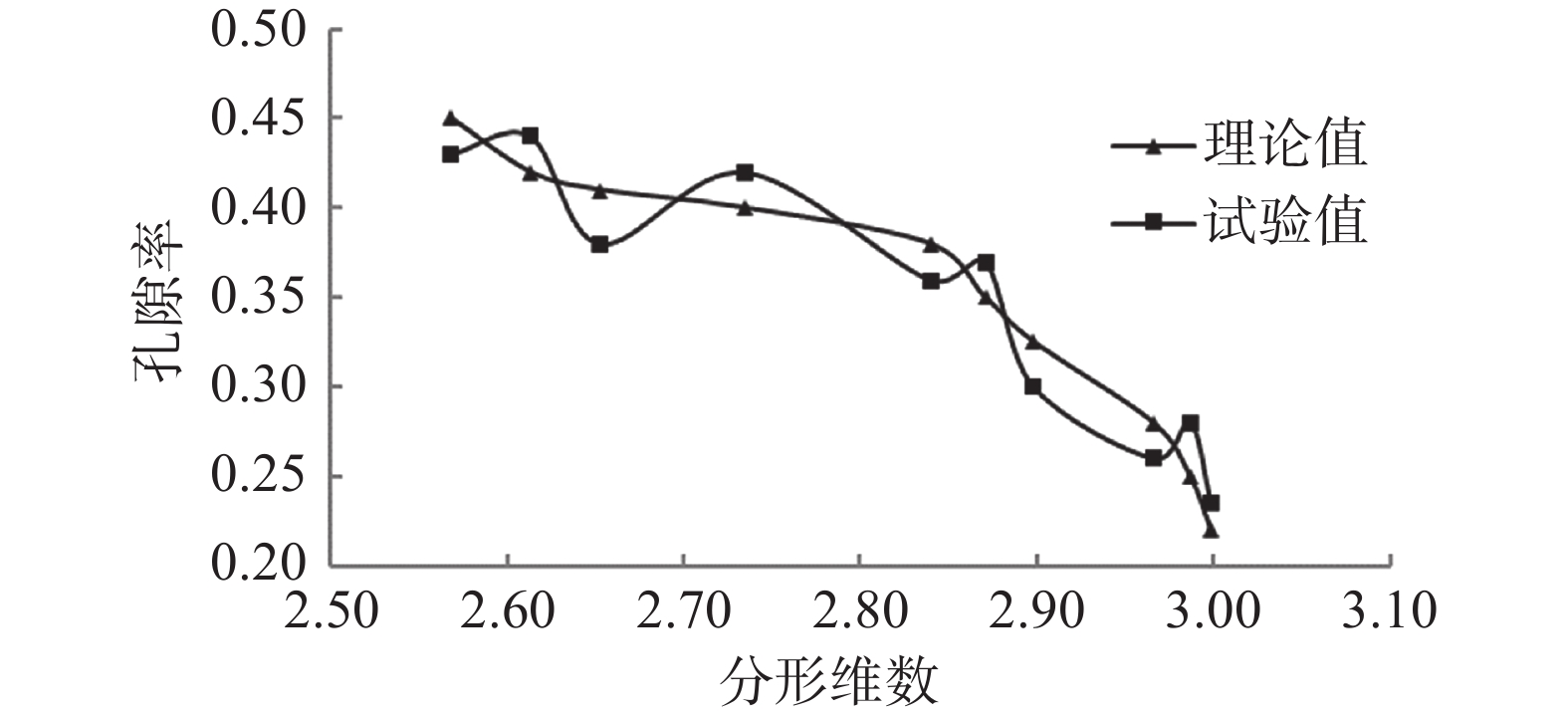
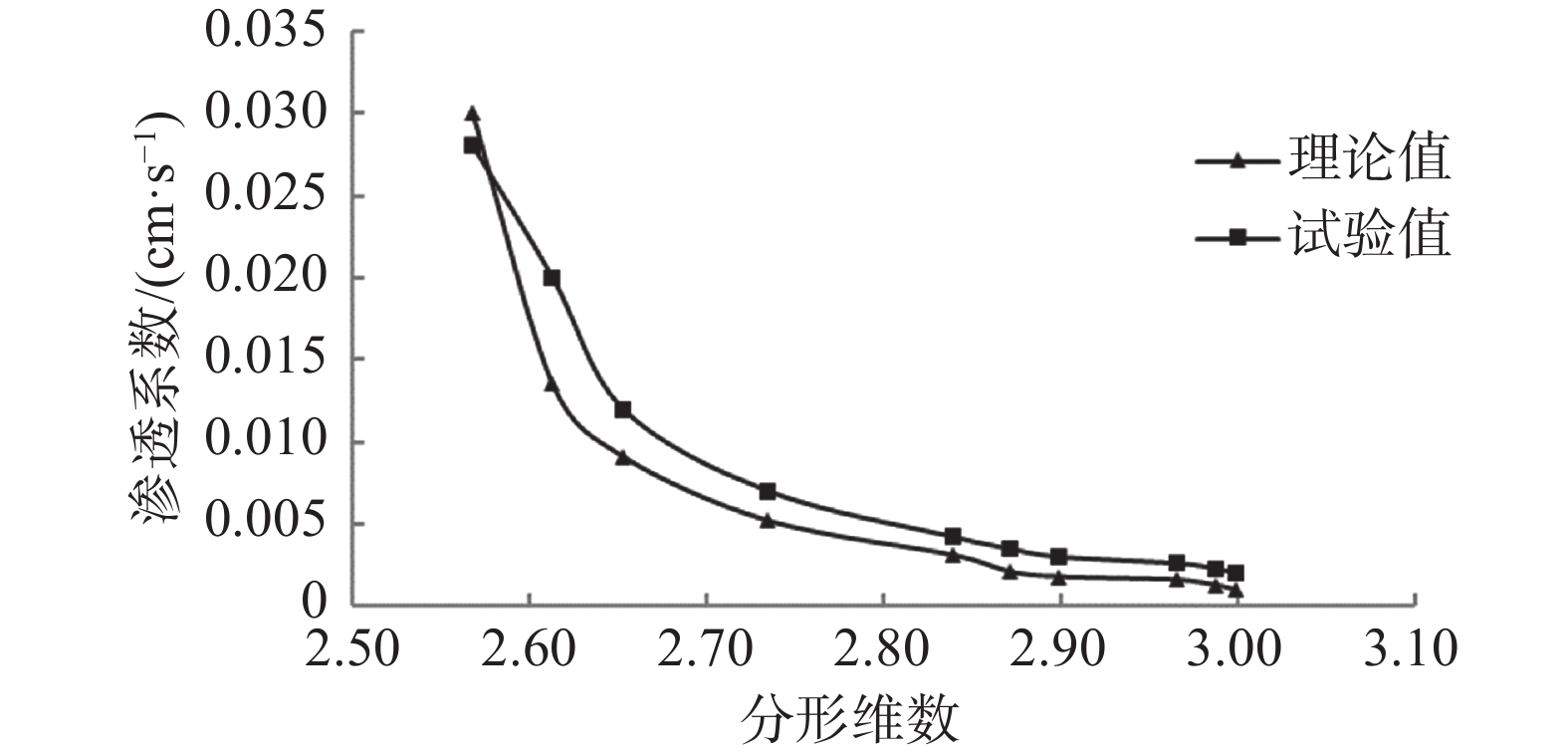
摘要: 堤坝工程渗流计算中确定土体渗透系数尤为重要。利用分形维数不同尺度域，分析渗透破坏试验土样无标度区，指出土体细颗粒含量是决定土体分形维数的主要因素。基于多孔介质毛管束模型，推导了渗透系数和孔隙率与分形维数之间分形关系解析式，阐释了多孔介质土体渗透系数影响因子包括分形系数、孔径大小、分形维数及流体黏滞系数。利用土体渗透破坏试验结果，进一步论证了渗透系数和孔隙率与分形维数之间的非线性关系。结果表明：当分形维数大于2.83时，孔隙率随着分形维数的增大而减小，但在颗粒吸着水和薄膜水形成的黏聚力影响下，渗透系数随着分形维数增大而减小的规律不明显。研究结果可为渗透破坏形成机制及发展过程分析提供理论依据，减少堤坝渗透破坏致灾隐患。Abstract: Permeability coefficient of soil is extremely important to dike and dam engineering. Scale-invariant space of seepage failure testing soils were statistically analyzed by multifractal dimensions, which shows that fine particle content is the major factor of mass fractal dimension. Based on a pipe bundle model of porous medium, the theoretical relationship between permeability coefficient and porosity was deduced, indicating that the influence factors of permeability coefficient include fractal coefficient, particle size, fractal dimension and fluid viscosity coefficient. The nonlinear relationship of permeability coefficient, porosity and fractal dimension was verified for further studies based on seepage failure experimental results. The results show that when the fractal dimension value is greater than 2.83, porosity decreases obviously with the increase of the fractal dimension, while permeability coefficient decreases insignificantly under the cohesive force of hydroscopic water and film water. The results provide a theoretical base for seepage formation mechanism and evolution process, which can decrease the seepage disaster risk of dams.
-
近年来，我国水库水体富营养化现象日益加剧，其污染源极其复杂，潜在的危害很大，已成为水环境保护中最突出的环境问题。三峡水库蓄水后，水库支流经常出现藻华，对当地水环境和生态构成了巨大挑战[1]。根据我国近几年的调查显示，一些大中型水库水体处于中度营养化到富营养化的过渡状态[2]。多个供水水库出现富营养化，其中包括上海重要饮用水水库——青草沙水库[3]。以往供水水库取水口设计主要考虑防沙、防浪、避咸、水质、温度分层、工程造价等因素[4-9]，尚未考虑从抑制蓝藻水华方面优化取水口位置。
水库富营养化控制除了减少氮磷营养盐输入、投放鳙鲢生物控藻、生态浮岛等措施外，缩短水库水体的水龄也是一项非常重要的措施。水龄可以定量反映水体的运动和交换程度及滞留情况，对评估水质变化具有重要意义。
水龄的概念来自于恒定流。假设一个与外界存在物质交换的容器，并假设物质交换过程是平衡态的，即物质的总质量和统计分布不随时间而变。Bolin等[10]在此基础上，将某种物质的水龄定义为该物质进入容器后所经历的时间。水龄的研究一般通过数学模型来实现。现有数学模型方法分为直接跟踪法和间接跟踪法两种。直接跟踪法采用拉格朗日法直接跟踪记录生命的水团运动过程[11-13]。该方法的缺点是计算量大，且跟踪多源水体时计算困难。在实际水体中，往往存在多个源和汇，有时还对不同水源进入的水体进行跟踪。为此，Deleersnijder等[14]提出了染色模拟计算水龄的通用理论，从而完善了间接跟踪的基本理论。
1. 水体水龄模拟方法及其改进
邵军荣曾基于染色模拟计算水龄的通用理论研发了无结构网格二维水龄计算模型[15]。美国环境保护署EPA研发的EFDC模型，适用面广，对湖库三维流动模拟精度高，多次应用于模拟水体水龄[16-19]。该模型代码编写模块化设计，改编非常方便，为适应三维分层计算，本文基于上述染色模拟计算水龄的原理，改进了EFDC模型。
Deleersnijder等定义c(t, x, τ)为与时间t、空间位置x和水龄τ相关的水龄谱，且在水体中符合守恒物质输运规律[14]。
$$ \frac{{\partial c}}{{\partial t}} = - \nabla \left({{{u}}c - k\nabla c} \right) $$ (1) 式中：u为流速矢量场（m/s）；k为扩散系数（m/s2）；c为c ( t , x , τ )函数。
定义水体中示踪物质含量C和水龄密度α：
$$ C\left({t,{{x}}} \right) = \int_0^\infty {c\left({t,{{x}},\tau } \right)} {\rm{d}}\tau $$ (2) $$ \alpha \left({t,\tau } \right) = \int_0^\infty {\tau c(t,{{x}},\tau ){\rm{d}}\tau } $$ (3) 基于以上定义，在t时刻、空间位置x处的平均水龄a(t,τ)可定义为：
$$ a\left({t,\tau } \right) = \frac{{\int_0^\infty {\tau c(t,{{x}},\tau ){\rm{d}}\tau } }}{{\int_0^\infty {c(t,{{x}},\tau ){\rm{d}}\tau } }}{\rm{ = }}\frac{\alpha }{C} $$ (4) 则有示踪物质浓度控制方程与水龄密度控制方程：
$$ \frac{{\partial C}}{{\partial t}} + {{u}}\nabla C - k{\nabla ^2}C = 0 $$ (5) $$ \frac{{\partial \alpha }}{{\partial t}} + {{u}}\nabla \alpha - k{\nabla ^2}\alpha = C $$ (6) 方程（5）和（6）解决了染色模拟与水龄模拟相关的理论。方程（6）为改进EFDC模型的关键方程，即在EFDC模型中添加一个水龄密度方程，该方程需要添加一个与示踪物质含量相关的源项。
为计算方便，示踪物质浓度在进入计算水域的边界上设为1.0 mg/L，故模型边界条件为：
$C = 1$ ；$\alpha {\rm{ = }}0$ 。2. 浏河水库取水泵站位置优化
2.1 各方案水流模拟
太仓市第三水厂位于二水厂东南方向16 km 处，水源地位于长江浏河口上游边滩浏河水库，现状布置如图1所示。水库总库容1 742万m3，有效库容1 427万m3，应急库容242万m3，死库容315万m3。最高蓄水位5.5 m，死水位−1.2 m，应急水位0 m，夏季运行水位0~1.5 m，水库库底标高−2.80 m，水面面积220万m2。三水厂取水时采用远期规划建设60万m3。
浏河水库运行以来，实际日供水不到20万m3，与设计供水能力差距较大。太仓三水厂为了缩短供水水库换水周期，将平均蓄水水位降至约1.0 m，对应库容约760万m3，换水周期约为38 d。由于换水周期较长，夏季高温期间水库水体富营养化程度加剧，水厂实测最高藻细胞数达到每升514万个。
太仓第二水厂水源地拟搬迁至本水库，可以提高水库的原水利用率，降低运行管理成本，缩短水库的换水周期。二水厂现状实际日供水量为20万m3，按照现行的水库运行管理方式，按实际供水量计算换水周期将缩短到约15 d。
浏河水库由于库容较大、用水量较小，导致水库原水流动性不高，加之水深较浅，水库内藻类易于繁殖。通过新建二水厂浏河取水及换水泵站，可与现有三水厂浏河取水泵站形成多点取水、统一换水的格局，有效提高水库原水的流动性，一定程度上可提高原水水质。同时，本工程取水及换水泵站还具有换水功能，当浏河水库需要换水改善水质时，可就近排出水库原水至长江，提高浏河水库原水水质。为了更科学地布置二水厂取水泵房和取水头的位置，充分利用取水产生的环流改善库区的流动特性，减轻水体富营养化，特进行取水方案优化研究。
水库水流往往受到风切应力、热浮力、取排水水量（源、汇项）等因素的控制。由于本工程所在水库水深较浅，最高蓄水位时水深仅8 m，夏季平均蓄水水深仅4 m，故热浮力作用甚微。由于水库面积较大，达到220万 m2，影响水流的主要因素为风，其次是取水形成的汇。由于浅水湖泊风生流会在湖泊平面及垂面上产生环流，表层水流方向与底层水流方向往往相反，所以对于风生流的模拟宜采用分层三维模型进行研究。
浏河水库形状基本规则，整个水库剖分成20 m×20 m的正方形网格，共布置5 504个网格单元。计算分成6层，每层厚度相等。计算时间步长10 s，水库地形采用清淤后的标高，基本为−2.80 m。计算初始水位采用夏季平均运行水位1.0 m。计算风速为太仓夏季平均风速3.6 m/s，风向为夏季主导风向SSE和SE。
本工程泵站取用浏河水库原水，应靠近浏河水库选址。由于现状第三水厂取水泵房位于浏河西侧中间区域，因此本工程新建取水泵站选址主要有3个方案。方案1~3泵站选址分别位于浏河水库东北角、西南角和西北角。
由于水库内水体流动性差，库区内水体的水龄也存在差异性。计算分析做了如下假定：（1）长期受SE向风或SSE向风影响，风速3.6 m/s；（2）水库初始运行水位为0 m，长江补充水库流量33.5 m3/s，补充长江水的同时，从水库取水供水，1.5 d后停止补充长江水；（3）水库供水流量为40万t/d，二水厂、三水厂各供水20万t/d；（4）每运行10 d补充长江水1次，每次补水持续时间1.5 d。
经数值模拟，得到了如图2所示的水库环流结构以及如图3所示的库区水龄分布情况。水库平均水龄及取水水域水龄统计如表1所示。
表 1 水库平均水龄及取水水域水龄统计Table 1. Water age of reservoir (average) and water intake area布置方案 库区平均
水龄/d二水厂取水
水域水龄/d三水厂取水
水域水龄/d方案1 20.0 13.5 11.9 方案2 16.3 23.2 10.1 方案3 20.4 11.8 11.9 ![]()
图 2 SE风3.6 m/s作用下库区环流Figure 2. Currents in the reservoir in a southeast wind with speed of 3.6 m/s![]()
图 3 SE风3.6 m/s作用下库区水龄分布（单位：d）Figure 3. Water age distribution in a southeast wind with speed of 3.6 m/s (unit: d)以上计算成果表明：
（1）二水厂泵房方案2有利于长江补充水与水库水体的充分混合，库区平均水龄由布置方案1和3的20 d缩短到16 d；方案1和3的2个布置方案对水库整体水龄和三水厂取水泵房以南库区水龄的影响很小，而对三水厂以北库区水龄的影响较大，主要表现在小于12 d的短水龄区分布差异较大。
（2）二水厂泵房采用方案1和方案3在水库的南部水域均形成较大面积的难换水区，水龄达到25 d以上的区域将达到约1/4库区面积。而采用布置方案2可以大大降低水库南部水域的水龄，与方案1和3相比，南部水域水龄基本可以缩短5 d。
2.2 取水泵站位置比较
下面综合分析3个取水泵站位置方案的优劣。
（1）夏季盛行风条件下，无论采用哪个布置方案，水库表层水体的流动方向均为从南往北方向流动，方案2布置在浏河水库西南角处于盛行风的上风口，上层水体的蓝藻不容易在取水水域聚集。
（2）二水厂泵房布置在浏河水库东北角或西北角时，取水主要来自库区东北角和东半部水库的水，这部分水体基本是新补入的长江水，而三水厂取水主要来自泵房附近的西半部水库的水体，这样水库的西南角水体很难得到新补入的长江水的混合，造成大量新水被取走而大量旧水得不到新水掺混。而采用方案2将泵房布置在浏河水库西南角时，二水厂取水主要来自三水厂泵房以南库区，三水厂取水主要来自三水厂泵房以北库区，有利于长江水在水库中整体掺混均匀后供水，库区平均水龄由方案1的20 d缩短到17 d。
（3）二水厂泵房布置在浏河水库东北角或西北角时，优点是取水水域离补充水出口较近，水龄为13 d；当二水厂取水头部发生藻华灾害时，立刻补入长江水，长江水只需2 d就能到达二水厂取水水域；换水泵通过穿堤暗管向长江排放，影响较小；缺点是取水水域处于下风口，不利于缩短库区的整体水龄，水库的西南角存在换水死角，水龄大于30 d。
（4）二水厂泵房布置在浏河水库西南角时，优点正好是布置在东北角的缺点。缺点是取水水域水龄较长，达到23 d，长江向水库补水后5～6 d才能影响取水水域，但是由于位于夏季盛行风的上风口，上层水体中的藻类不容易在取水水域聚集。总体而言，方案2有利于改善二水厂取水水质。
（5）二水厂采用方案2时增设换水泵效果明显，而采用方案1和3时，换水泵对南部水域水龄的缩短效果不明显。采用方案2时，二水厂增设换水泵流量达到1.7 m3/s（即15万m3/d）时，在夏季盛行风条件下，库区平均水龄由17 d缩短到12 d，南部水域水龄将缩短到13 d。考虑到夏季风向不可能恒定，实际南部水域水龄比计算结果要短，故换水泵流量达到15万m3/d时，基本可以达到库区水龄小于15 d的要求。采用方案1和3时，增设换水泵在夏季特殊时期持续运行以期缩短库区水龄的措施是不经济的，建议采取应急补充长江水的方式抑制水华，然后择机运行至死水位，三水厂取用长江水继续供水，二水厂停止供水，利用排空泵排空水库进行彻底换水。
综上所述，从库区环流及水龄等环境水力学角度出发，方案2（二水厂泵房位于浏河水库西南角）明显优于方案1和3。
3. 结 语
水库的氮磷营养盐输入量、水深、气温等自然条件难以控制，通过优化取水泵房位置可以改变水库环流特性，缩短水库水龄；通过长江水抑制蓝藻的生长，从而降低水库富营养化的风险，这是比较现实的措施。基于染色模拟的水龄模拟方法能较少地改动成熟模型的代码，有效模拟库区、湖泊水龄，是一种基于水龄优化水库进排水设计抑制蓝藻水华的有效方法。
著作权使用声明
本刊已许可中国知网、维普资讯、万方数据、博看网、超星数据、中教数据库、中邮阅读网等以数字化方式复制、汇编、发行、信息网络传播本刊全文。本刊支付的稿酬已包含中国知网、维普资讯、万方数据、博看网、超星数据、中教数据库、中邮阅读网等著作权使用费，所有署名作者向本刊提交文章发表之行为视为同意上述声明。如有异议，请在投稿时说明，本刊将按作者说明处理。
《水利水运工程学报》编辑部
2020-03-20
-
![]()
图 5 土体分形维数和孔隙率理论值与试验值对比
Figure 5. Comparison between theoretical values and experimental results of soil fractal dimension and porosity
![]()
图 6 土体分形维数和渗透系数理论值与试验值对比
Figure 6. Comparison between theoretical values and experimental results of soil fractal dimension and permeability coefficient
表 1 不同试验土样颗粒级配
Table 1 Particle size distribution of different experimental soils
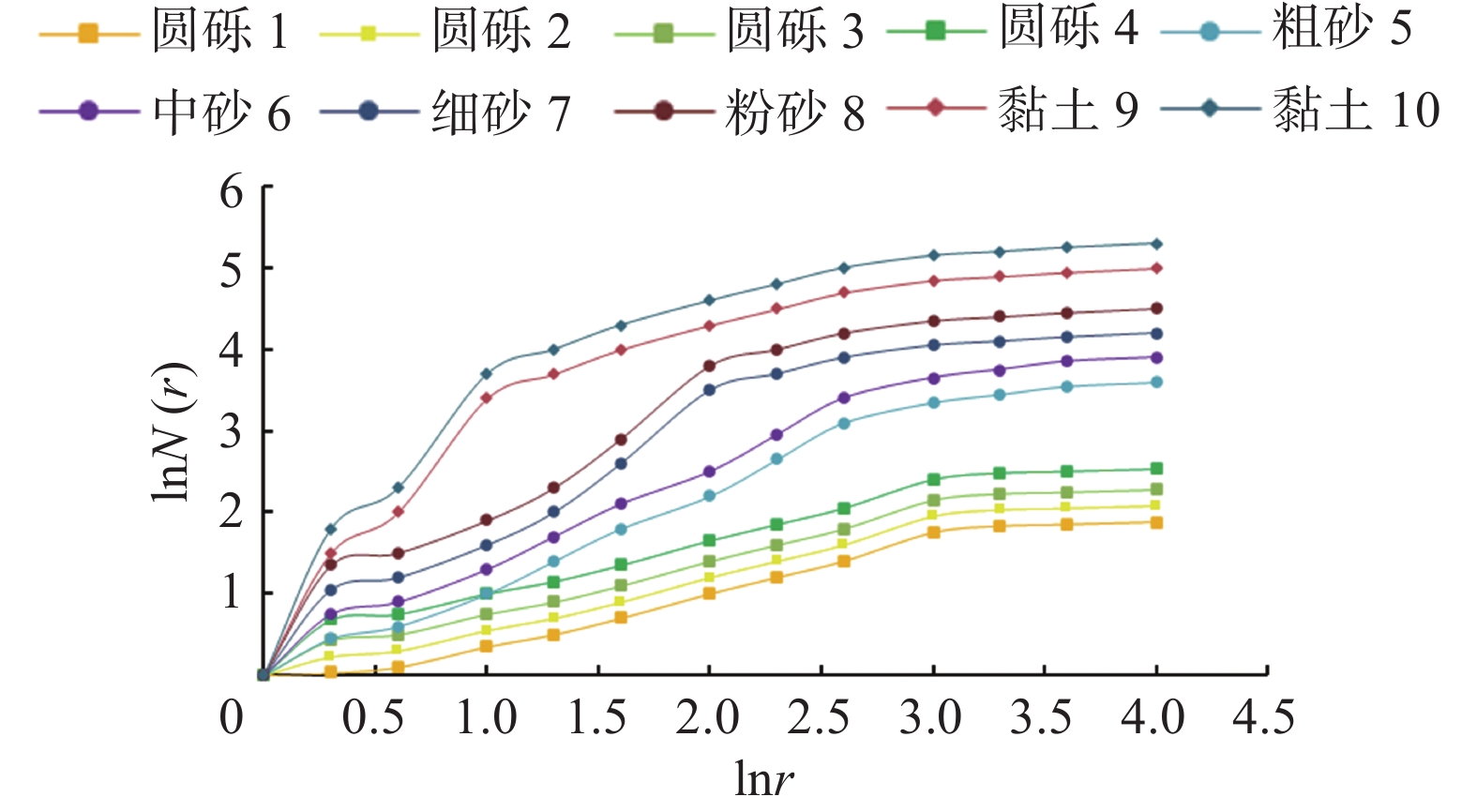
土样 不同粒径区间质量百分比/% >20 mm 20~10 mm 10~5 mm 5~2 mm 2~1 mm 1~0.5 mm 0.5~0.25 mm 0.25~0.10 mm 0.10~0.075 mm 0.075~0.025 mm <0.025 mm 1 5.37 19.98 26.38 16.68 8.96 8.61 8.22 4.80 0.70 0.21 0.09 2 8.32 17.92 29.97 15.85 9.12 8.55 8.34 1.80 0.08 0.04 0.01 3 7.32 20.32 30.73 14.97 11.45 10.23 3.23 1.47 0.20 0.06 0.02 4 6.85 19.42 26.56 18.54 13.22 9.43 4.18 1.70 0.07 0.02 0.01 5 2.58 10.80 15.42 15.94 17.32 20.30 12.64 4.70 0.20 0.08 0.02 6 1.16 5.30 9.70 9.93 11.22 19.37 18.32 14.55 8.45 1.98 0.02 7 / / / 0.30 1.80 6.80 22.12 35.30 20.38 8.21 5.09 8 / / / / 0.10 2.34 11.23 32.21 33.28 15.20 5.64 9 / / / / / / / / 0.87 2.11 97.02 10 / / / / / / / / 4.91 10.67 84.42 注：编号1~4为圆砾，5~8为砂，9~10为黏土。 
下载: 导出CSV
表 2 不同试验土样质量分形维数与无标度区统计结果
Table 2 Statistical results of mass fractal dimension and scale-invariant space of different experimental soils
土样编号 土样类别 无标度区/mm 无标度区土体
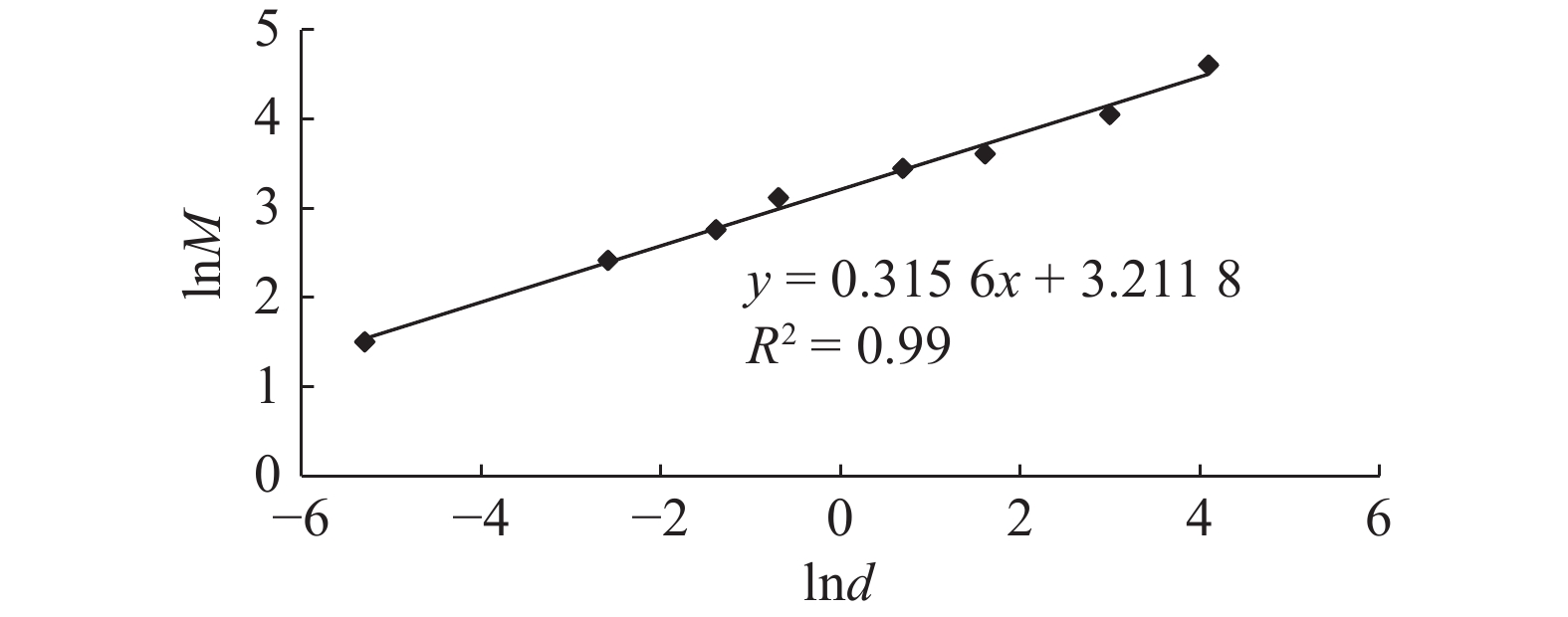
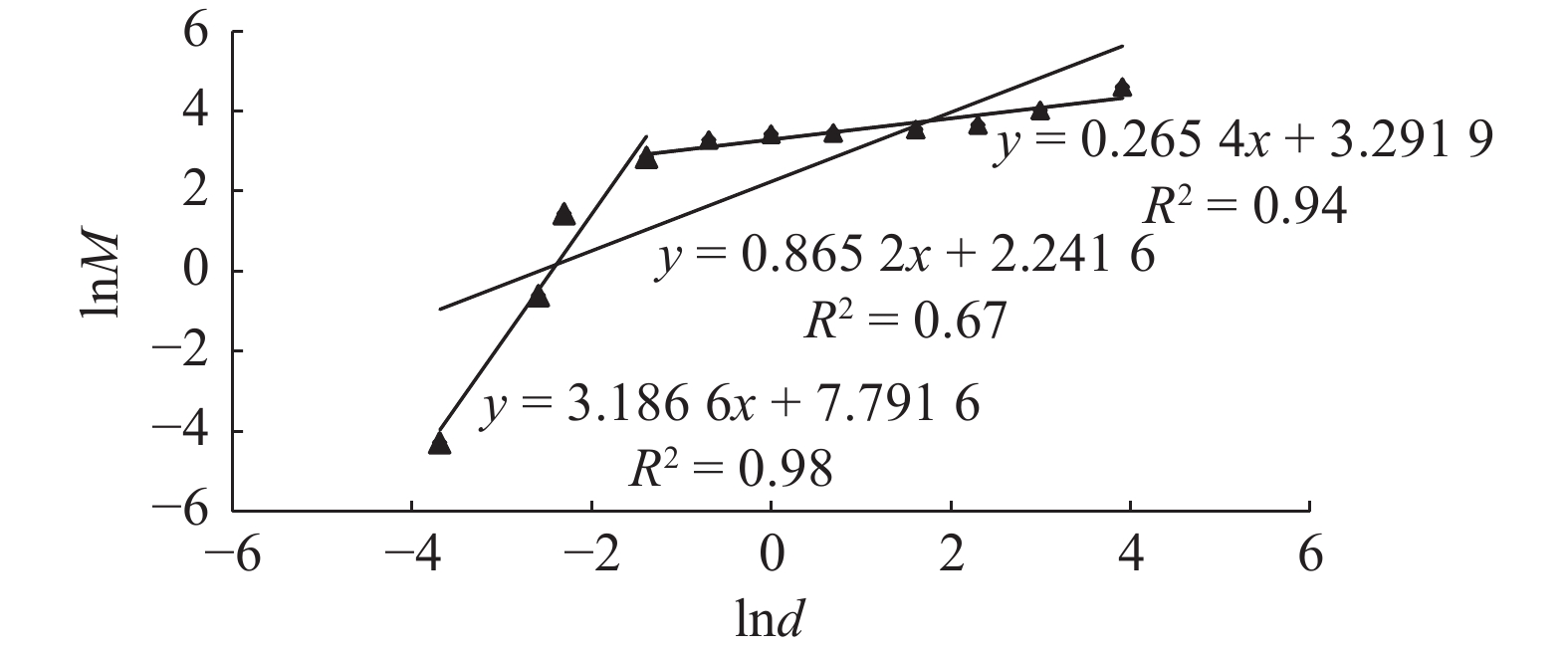
颗粒含量/%分形维数 相关系数 下限 上限 1 圆砾 0.250 20.000 88.83 2.652 6 0.954 3 2 圆砾 0.250 20.000 89.75 2.734 6 0.881 2 3 圆砾 0.500 20.000 87.70 2.613 0 0.993 7 4 圆砾 0.500 20.000 87.17 2.567 8 0.984 1 5 粗砂 0.500 10.000 68.98 2.870 9 0.996 1 6 中砂 0.250 10.000 68.54 2.839 5 0.936 9 7 细砂 0.100 0.500 57.42 2.898 2 0.789 6 8 粉砂 0.075 0.250 65.49 2.999 0 0.906 6 9 黏土 0.002 0.005 97.02 2.995 1 0.903 9 10 黏土 0.002 0.005 84.42 2.966 0 0.882 1
下载: 导出CSV
-
[1] MANDELBROT B B. Fractal: Form, chance and dimension[M]. San Francisco: Freeman, 1977.
[2] OUYANG M, TAKAHASHI A. Influence of initial fines content on fabric of soils subjected to internal erosion[J]. Canadian Geotechnical Journal, 2016, 53(2): 299-313. doi: 10.1139/cgj-2014-0344
[3] ISRAR J, INDRARATNA B. Study of critical hydraulic gradients for seepage-induced failures in granular soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2019, 145(7): 04019025. doi: 10.1061/(ASCE)GT.1943-5606.0002062
[4] WANG Y, WANG S J, DUAN X B, et al. Physical modelling of initial seepage failure process[J]. International Journal of Physical Modelling in Geotechnics, 2015, 15(4): 1-9.
[5] 陈建生, 何文政, 王霜, 等. 双层堤基管涌破坏过程中上覆层渗透破坏发生发展的试验与分析[J]. 岩土工程学报,2013,35(10):1777-1783. (CHEN Jiansheng, HE Wenzheng, WANG Shuang, et al. Laboratory tests on development of seepage failure of overlying layer during piping of two-stratum dike foundation[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(10): 1777-1783. (in Chinese) CHEN Jiansheng, HE Wenzheng, WANG Shuang, et al. Laboratory tests on development of seepage failure of overlying layer during piping of two-stratum dike foundation[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(10): 1777-1783. (in Chinese)
[6] 朱晟, 邓石德, 宁志远, 等. 基于分形理论的堆石料级配设计方法[J]. 岩土工程学报,2017,39(6):1151-1155. (ZHU Sheng, DENG Shide, NING Zhiyuan, et al. Gradation design method for rockfill materials based on fractal theory[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(6): 1151-1155. (in Chinese) doi: 10.11779/CJGE201706023 ZHU Sheng, DENG Shide, NING Zhiyuan, et al. Gradation design method for rockfill materials based on fractal theory[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(6): 1151-1155. (in Chinese) doi: 10.11779/CJGE201706023
[7] 王宇, 王士军, 谷艳昌. 基于分形理论的多孔介质渗透破坏研究[J]. 中国农村水利水电,2016(3):80-83, 87. (WANG Yu, WANG Shijun, GU Yanchang. Research on seepage failure in porous media based on fractal theory[J]. China Rural Water and Hydropower, 2016(3): 80-83, 87. (in Chinese) doi: 10.3969/j.issn.1007-2284.2016.03.019 WANG Yu, WANG Shijun, GU Yanchang. Research on seepage failure in porous media based on fractal theory[J]. China Rural Water and Hydropower, 2016(3): 80-83, 87. (in Chinese) doi: 10.3969/j.issn.1007-2284.2016.03.019
[8] KONG X X, LIU Q S, LU H F. Effects of rock specimen size on mechanical properties in laboratory testing[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2021, 147(5): 04021013. doi: 10.1061/(ASCE)GT.1943-5606.0002478
[9] YOUSEFI M, SEDGHI-ASL M, PARVIZI M. Seepage and boiling around a sheet pile under different experimental configuration[J]. Journal of Hydrologic Engineering, 2016, 21(12): 06016015. doi: 10.1061/(ASCE)HE.1943-5584.0001449
[10] 卞士海, 李国英, 米占宽. 分形理论在堆石料流变中的应用[J]. 水利水运工程学报,2017(6):60-68. (BIAN Shihai, LI Guoying, MI Zhankuan. Application of fractal theory in rockfill rheology[J]. Hydro-Science and Engineering, 2017(6): 60-68. (in Chinese) BIAN Shihai, LI Guoying, MI Zhankuan. Application of fractal theory in rockfill rheology[J]. Hydro-Science and Engineering, 2017(6): 60-68. (in Chinese)
[11] 王宇, 陈超, 陈祥勇. 土石坝渗流安全预测预警研究[J]. 水利水电技术,2018,49(11):68-74. (WANG Yu, CHEN Chao, CHEN Xiangyong. Study on prediction and early-warning of seepage safety for earth-rockfill dam[J]. Water Resources and Hydropower Engineering, 2018, 49(11): 68-74. (in Chinese) WANG Yu, CHEN Chao, CHEN Xiangyong. Study on prediction and early-warning of seepage safety for earth-rockfill dam[J]. Water Resources and Hydropower Engineering, 2018, 49(11): 68-74. (in Chinese)
[12] 谢和平. 分形几何及其在岩土力学中的应用[J]. 岩土工程学报,1992,14(1):14-24. (XIE Heping. Fractal geometry and its application to rock and soil materials[J]. Chinese Journal of Geotechnical Engineering, 1992, 14(1): 14-24. (in Chinese) doi: 10.3321/j.issn:1000-4548.1992.01.002 XIE Heping. Fractal geometry and its application to rock and soil materials[J]. Chinese Journal of Geotechnical Engineering, 1992, 14(1): 14-24. (in Chinese) doi: 10.3321/j.issn:1000-4548.1992.01.002
[13] RAMADAN S H, EL NAGGAR M H. Field monitoring and numerical analysis of large-span three-sided reinforced concrete culvert[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2021, 147(4): 04021008. doi: 10.1061/(ASCE)GT.1943-5606.0002489
[14] 徐永福, 黄寅春. 分形理论在研究非饱和土力学性质中的应用[J]. 岩土工程学报,2006,28(5):635-638. (XU Yongfu, HUANG Yinchun. Fractal-textured soils and their unsaturated mechanical properties[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(5): 635-638. (in Chinese) doi: 10.3321/j.issn:1000-4548.2006.05.017 XU Yongfu, HUANG Yinchun. Fractal-textured soils and their unsaturated mechanical properties[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(5): 635-638. (in Chinese) doi: 10.3321/j.issn:1000-4548.2006.05.017
[15] TAO G L, WU X K, XIAO H L, et al. A unified fractal model for permeability coefficient of unsaturated soil[J]. Fractals, 2019, 27(1): 1940012. doi: 10.1142/S0218348X19400127
[16] 段祥宝, 刘运化, 杨超, 等. 土体渗透变形及渗透破坏过程中分形特征初探[J]. 水电能源科学,2013,31(7):100-103, 214. (DUAN Xiangbao, LIU Yunhua, YANG Chao, et al. Preliminary study on fractal law of levees soil seepage deformation and failure[J]. Water Resources and Power, 2013, 31(7): 100-103, 214. (in Chinese) DUAN Xiangbao, LIU Yunhua, YANG Chao, et al. Preliminary study on fractal law of levees soil seepage deformation and failure[J]. Water Resources and Power, 2013, 31(7): 100-103, 214. (in Chinese)
[17] 陶高梁, 李进, 崔惜琳. 不同颗粒级配的砂土渗流破坏特性[J]. 土木工程与管理学报,2019,36(2):90-97. (TAO Gaoliang, LI Jin, CUI Xilin. Seepage failure characteristics of sand with different grain composition[J]. Journal of Civil Engineering and Management, 2019, 36(2): 90-97. (in Chinese) doi: 10.3969/j.issn.2095-0985.2019.02.014 TAO Gaoliang, LI Jin, CUI Xilin. Seepage failure characteristics of sand with different grain composition[J]. Journal of Civil Engineering and Management, 2019, 36(2): 90-97. (in Chinese) doi: 10.3969/j.issn.2095-0985.2019.02.014
[18] RICHARDS K S, REDDY K R. Experimental investigation of initiation of backward erosion piping in soils[J]. Geotechnique, 2012, 62(10): 933-942. doi: 10.1680/geot.11.P.058
[19] KIM H J, PARK J M, SHIN J H. Flow behaviour and piping potential at the soil-structure interface[J]. Geotechnique, 2019, 69(1): 79-84. doi: 10.1680/jgeot.17.T.020
[20] 王小杰, 姜仁贵, 解建仓, 等. 基于分形和R/S分析的渭河干流径流变化特征研究[J]. 水利水运工程学报,2019(1):102-108. (WANG Xiaojie, JIANG Rengui, XIE Jiancang, et al. Analysis of runoff variation characteristics in the mainstream of Weihe River based on fractal theory and R/S analysis method[J]. Hydro-Science and Engineering, 2019(1): 102-108. (in Chinese) WANG Xiaojie, JIANG Rengui, XIE Jiancang, et al. Analysis of runoff variation characteristics in the mainstream of Weihe River based on fractal theory and R/S analysis method[J]. Hydro-Science and Engineering, 2019(1): 102-108. (in Chinese)
[21] 刘星志, 吴悦, 潘诗婷, 等. 颗粒级配对非饱和红土土-水特征曲线的影响[J]. 水利水运工程学报,2018(5):103-110. (LIU Xingzhi, WU Yue, PAN Shiting, et al. Influences of different grain size contents on soil-water characteristic curve of unsaturated laterite based on fractal theory[J]. Hydro-Science and Engineering, 2018(5): 103-110. (in Chinese) LIU Xingzhi, WU Yue, PAN Shiting, et al. Influences of different grain size contents on soil-water characteristic curve of unsaturated laterite based on fractal theory[J]. Hydro-Science and Engineering, 2018(5): 103-110. (in Chinese)
[22] TURCOTTE D L. Fractals and fragmentation[J]. Journal of Geophysical Research, 1986, 91(B2): 1921-1926. doi: 10.1029/JB091iB02p01921
[23] TYLER S W, WHEATCRAFT S W. Fractal scaling of soil particle-size distributions: analysis and limitations[J]. Soil Science Society of America, 1992, 56(2): 362-369. doi: 10.2136/sssaj1992.03615995005600020005x
[24] 王宇. 土石坝渗流分形特性与预警模型研究[D]. 南京: 南京水利科学研究院, 2017. WANG Yu. Study on seepage fractal characteristics and early-warning model of earth-rockfill dam[D]. Nanjing: Nanjing Hydraulic Research Institute, 2017. （in Chinese）
[25] 刘炳瑞, 林建忠. 多颗粒在Giesekus流体Poiseuille流场中的异常迁移[J]. 水动力学研究与进展,2021,36(1):1-4. (LIU Bingrui, LIN Jianzhong. Abnormal migration of multi-particles in Poiseuille flow of Giesekus fluid[J]. Chinese Journal of Hydrodynamics, 2021, 36(1): 1-4. (in Chinese) LIU Bingrui, LIN Jianzhong. Abnormal migration of multi-particles in Poiseuille flow of Giesekus fluid[J]. Chinese Journal of Hydrodynamics, 2021, 36(1): 1-4. (in Chinese)
-
期刊类型引用(4)
1. 吴永妍，李书友，郭辉，刘少华，黄明海. 南水北调中线沉藻池布置方案优化. 南水北调与水利科技(中英文). 2024(04): 798-809 . 
百度学术
2. 陈思绪，崔婧嫄，黄熠丽，张海平. 基于水龄的陈行水库流场特征分析. 净水技术. 2023(03): 60-66+119 . 百度学术
3. 刘莉，程香菊，肖舒元，庄美琪. 引水型水库叶绿素a对水龄响应的模拟研究. 中国防汛抗旱. 2022(S1): 179-186 . 百度学术
4. 黄爱平，刘晓波，彭文启，董飞，韩祯，王伟杰. 鄱阳湖水龄时空特征和影响因素分析. 水利学报. 2021(09): 1082-1090 . 百度学术
其他类型引用(3)
计量
- 文章访问数:
- HTML全文浏览量:
- PDF下载量:
- 被引次数: 7
