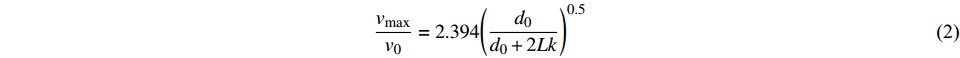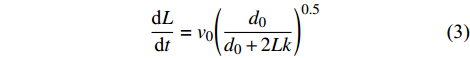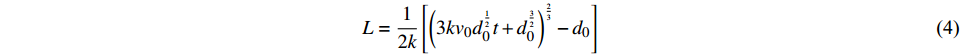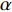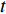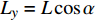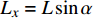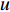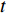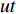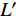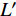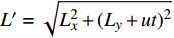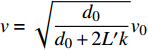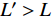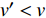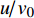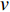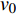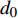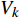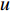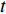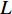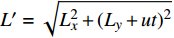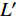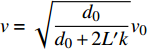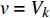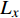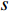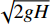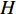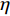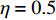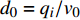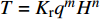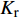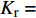Prediction of river scour in downstream of bankside parallel spillway tunnel
-
摘要: 挑流水舌对下游河道的冲刷关系到工程安全。根据动量方程推导了射流在下游水垫中的扩散规律,分析了下游水垫流速对射流扩散的影响,提出了动水垫下射流的临底流速计算方法。研究结果表明:动水流速增加了射流在水中的扩散距离,促进了射流扩散及射流流速衰减,降低了射流临底流速。将研究结果应用于白鹤滩岸边泄洪洞下游河道的冲坑深度预测。模型试验结果表明:在鼻坎水流参数相同的情况下,河道中水流为动水时的冲坑深度较静水时冲坑深度减小约10%,且位于河道下游侧的挑流水舌形成的冲坑深度小于上游侧挑流水舌形成的冲坑深度。与常规预测公式相比,该方法能准确预测不同位置挑流水舌的冲坑深度,研究结果可为泄洪设施下游河道消能防冲设计提供依据。Abstract: The river scouring caused by air jet is important to engineering safety. In this paper, the diffusion law of jet flow in downstream water cushion is deduced based on momentum equation, the influence of water cushion velocity on jet diffusion is analyzed, and the calculation method of bottom velocity under moving water cushion is proposed. It is shown that the moving water cushion increases the jet diffusion distance, promotes the jet diffusion and the jet velocity attenuation, and reduces the bottom velocity. The results of the research are applied to the prediction of the depth of the flushing pit downstream of the spillway tunnel of the Baihetan project. It is shown that the scour depth under the condition of moving water cushion is about 10% less than that under the condition of still water, and the depth of the scour pit formed by the flow on the downstream side of the channel is smaller than that formed by the flow on the upstream side of the river. The method proposed in this paper can well predict the depth of the scour pit at different locations, and the experimental results are in good agreement with the calculated results. The research results can provide a basis for the energy dissipation and anti-scour design of the downstream channel of flood discharge facilities.
-
Keywords:
- energy dissipation /
- coastal flood discharge /
- plunge pool /
- moving water cushion /
- air jet
-
挑射水流对下游河道的冲刷与射流入水扩散规律直接相关,射流入水后,主流在下游水体中不断扩散,主流流速随着射流扩散迅速降低。关于射流在水中的扩散规律已有较多的研究,Calitz[1]通过试验得出,射流入水后的外扩散角为14°~18°;Maleki等[2]在水槽中进行了射流与板块上举力的试验,认为水舌厚度与水舌扩散长度的比值是影响射流临底冲击压力的主要因素;Duarte等[3]引入掺气因素对射流冲坑模型进行了修正,认为掺气效应同时降低了冲击区的时均压力与脉动压力;Bollaert等[4-6]研究了射流引起岩石破坏的过程,指出掺气程度对冲坑发展有显著的影响;Schmocker等[7]的模型试验结果表明射流在空气中与在水中类似,外缘不断扩散,核心区域不断收缩,这种空中扩散效果与水流流速有关,对于原型水流,外缘扩散与核心区域收缩会更加明显;孙建等[8-11]也针对单股射流扩散做了较系统的试验,得出了射流入水后的流速及压力分布;辜晋德等[12]对比了不同比尺模型上的挑流水舌入水形态,认为大尺度模型的水舌扩散形态更为明显。多股射流入水时,由于水流互相干扰,流态更为复杂。刘沛清等[13]应用激光片源和荧光染色技术测量了多股射流入水的流场,分析了多股射流在水垫塘内的流动特征,提出了“动水垫”的概念;焦爱萍等[14]通过数值模型分析了多股射流在水垫塘内的流动特性,认为保持多股射流一定的入水间距可以减轻射流对水垫塘的动水压力。
大型水利枢纽的岸边泄洪洞承担着分洪消能的任务,大多布置在枢纽下游地质条件较好、地形较开阔处,并采用挑流的消能形式。与坝身泄洪消能不同,岸边泄洪洞往往布置在拦河坝下游,受到河道上游来流的影响,其消能区水体并非静水。同时岸边泄洪洞大多为并联布置,联合运行时射流水体之间互相干扰碰撞,流态较为复杂。系统分析并联射流在水体中的流动特性,对研究泄洪消能时的河道冲刷及边坡安全具有重要意义。本文以射流水舌为研究对象,从理论上分析下游动水流速对射流扩散的影响,结合动床物理模型试验,研究岸边泄洪洞并联运行时下游河道的冲刷形态,并提出动水条件下的河道冲坑深度计算方法。
1. 射流入水扩散规律
一般采用动量积分的方法研究射流,沿着射流方向上动量守恒(如图1),有
$ \;\rho v_0^2{d_0} = \rho {v^2}d $ ,其中:ρ为水的密度;$ {v_0} $ 为射流入水时的平均流速;$ {d_0} $ 为射流入水时的水舌宽度;$ v $ 为沿着射流方向与入水点距离为L的断面平均流速;$ d $ 为v流速断面对应的水舌宽度。θ为射流边界单侧扩散角度,则射流在水中的宽度与流程L存在以下关系:$ d = {d_0} + 2L\tan \theta $ ,令$ \tan \theta $ =$ k $ ,则有:$$ \frac{v}{{{v_0}}} = {\left( {\frac{{{d_0}}}{{{d_0} + 2Lk}}} \right)^{0.5}} $$ (1) 根据文献[1]的研究结果,取单侧扩散角θ为16°,则k=0.28,则式(1)代表射流在水中任意断面平均流速与入水平均流速的关系。根据相关文献[10-11],射流断面流速分布基本符合正态分布,则有断面最大流速vmax与断面平均流速关系为
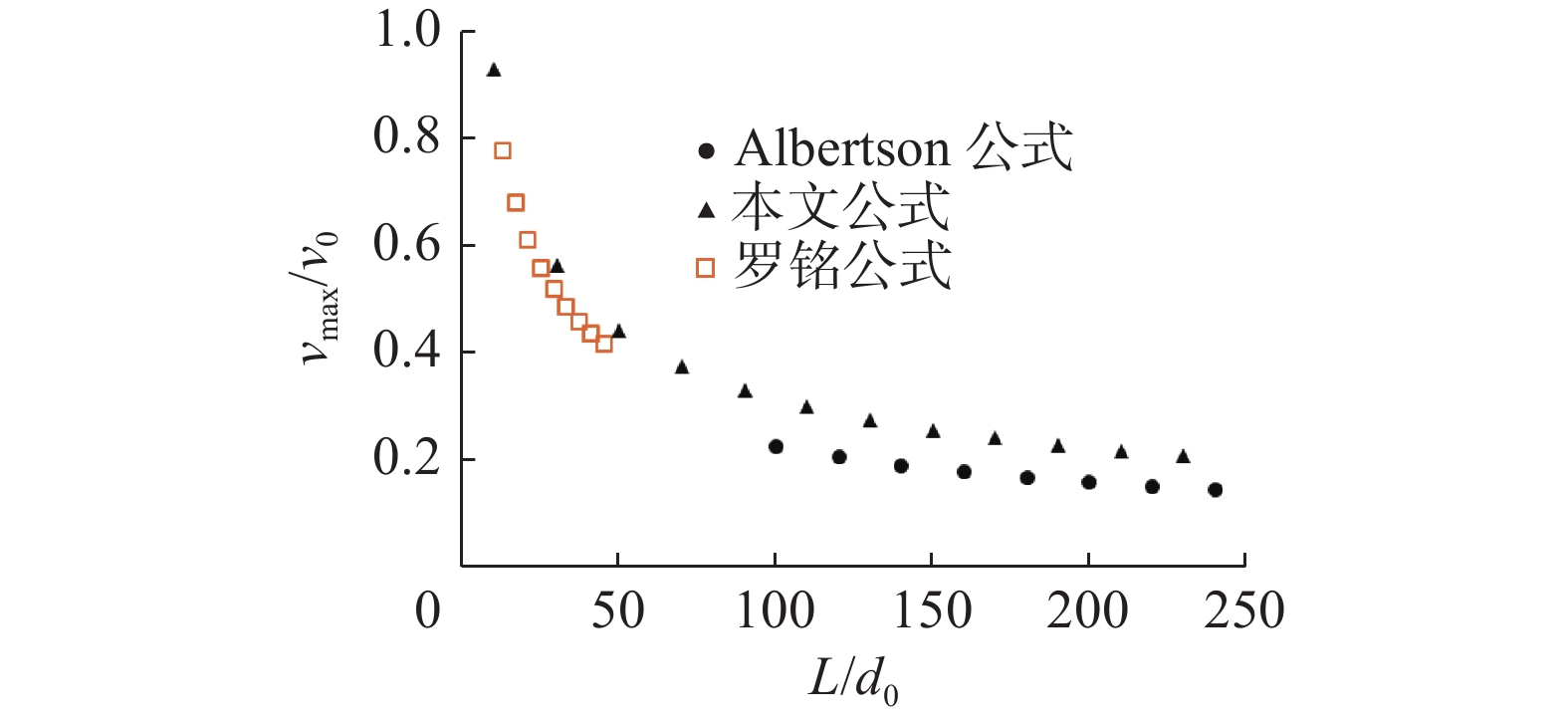
$ {v_{\max }} \approx 2.394v $ ,可得:$$ \frac{{{v_{\max }}}}{{{v_0}}} = 2.394{\left( {\frac{{{d_0}}}{{{d_0} + 2Lk}}} \right)^{0.5}} $$ (2) 式(2)计算结果与文献[11, 15]经验式计算结果对比见图2。从图2可以看出,本文计算式结果与文献的试验拟合结果较为接近,说明式(2)合理。
根据式(1)建立射流流程与入水流速的微分方程有:
$$ \frac{{{\text{d}}L}}{{{\text{d}}t}} = {v_0}{\left( {\frac{{{d_0}}}{{{d_0} + 2Lk}}} \right)^{0.5}} $$ (3) 经过变换,对等式两侧积分,引入待定常数项,并根据边界条件t=0时,L=0,可得:
$$ L = \frac{1}{{2k}}\left[ {{{\left( {3k{v_0}d_0^{\frac{1}{2}}t + d_0^{\frac{3}{2}}} \right)}^{\frac{2}{3}}} - {d_0}} \right] $$ (4) 式(4)即射流入水后扩散流程与时间关系式。
对于斜向入射的射流,其扩散流程同样符合式(4)。图3为斜向射流扩散示意图,斜向射流入射角度为
$ \alpha $ ,当下游水垫为静水时,则射流在下游水体中的扩散轨迹为直线,射流在$ t $ 时刻的位移为L,沿着水平$ y $ 方向的位移$ {L_y} = L\cos \alpha $ ,垂向位移$ {L_x} = L\sin \alpha $ 。当下游水体以流速$ u $ 水平流动,则射流在沿程扩散的同时,受到下游水体带动而整体移动,若射流从入水到触底的时间过程为$ t $ ,则射流受下游水体带动水平移动距离为$ ut $ ,射流实际运动轨迹为$ L' $ 。横向水流作用下的射流运动轨迹长度$ L' $ 可近似按$ L' = \sqrt {L_x^2 + {{({L_y} + ut)}^2}} $ 计算,临底流速按$ v = \sqrt {\dfrac{{{d_0}}}{{{d_0} + 2L'k}}} {v_0} $ 计算。射流流速衰减与射流运动轨迹相关,由于$ L' > L $ ,因此$ v' < v $ ,即横向水流进一步促进了射流扩散,降低了射流的临底流速。取入射角度
$ \alpha $ 为60°,以横向流速$ u $ 为参数,绘制了$ {{v'} \mathord{\left/ {\vphantom {{v'} v}} \right. } v} $ 随射流垂向距离$ {{{L_x}} \mathord{\left/ {\vphantom {{{L_x}} {{d_0}}}} \right. } {{d_0}}} $ 变化规律(图4)。从图4可以看出,动水的影响效果随着射流距离的增大而增大,当$ {u \mathord{\left/ {\vphantom {u {{v_0}}}} \right. } {{v_0}}} $ =0.3,在$ {{{L_x}} \mathord{\left/ {\vphantom {{{L_x}} {{d_0}}}} \right. } {{d_0}}} $ =50位置,射流断面平均流速$ v' $ 比静水条件下断面流速$ v $ 降低约30%。当预测射流形成的冲坑深度时,主要计算参数为射流入水流速
$ {v_0} $ 、入水宽度$ {d_0} $ 、河床基岩抗冲流速$ {V_k} $ 及下游河道流速$ u $ ,根据式(4)泄洪水舌入水参数计算不同时间$ t $ 时刻射流的扩散距离$ L $ ,根据$ L' = \sqrt {L_x^2 + {{({L_y} + ut)}^2}} $ 将扩散距离修正为动水作用后的实际扩散距离$ L' $ ,并以$ v = \sqrt {\dfrac{{{d_0}}}{{{d_0} + 2L'k}}} {v_0} $ 计算该时刻射流流速,当$ v = {V_k} $ 时认为冲坑达到平衡,相应时刻的$ {L_x} $ 即为冲坑深度。该方法通过水舌入水参数及河道抗冲流速计算冲坑深度,同时考虑了河道水流流速的作用,计算结果更为准确。2. 并联式岸边泄洪洞下游冲刷试验
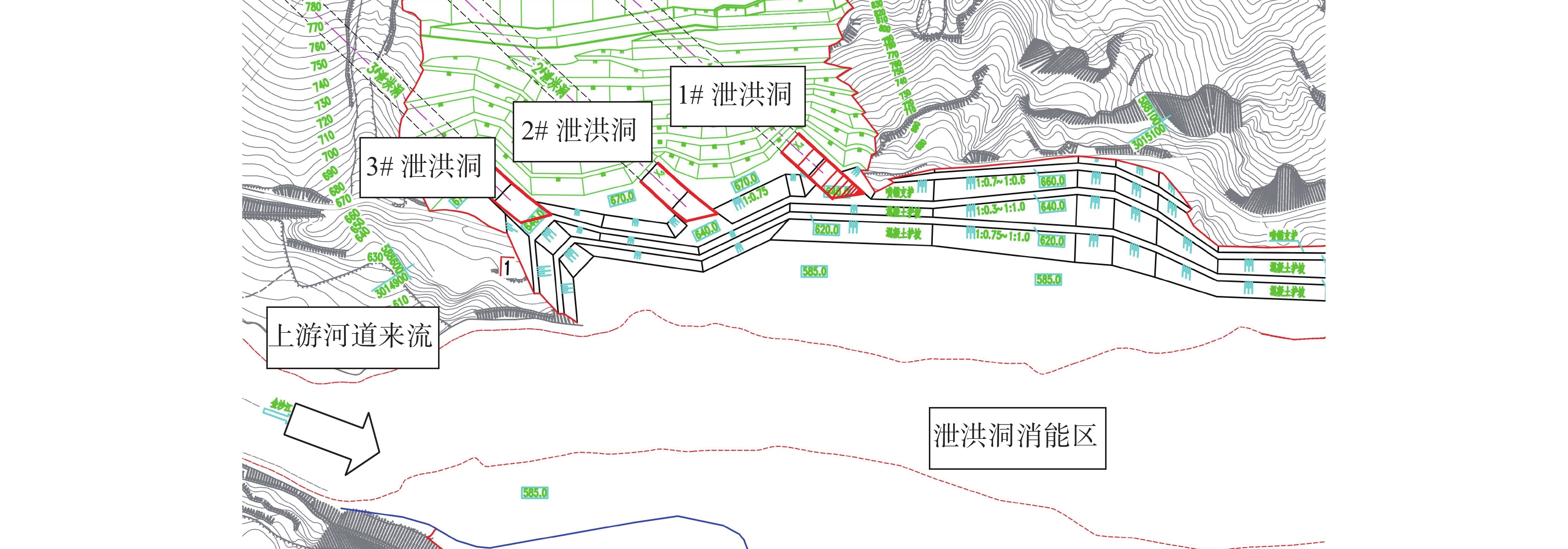
位于我国西南地区的白鹤滩水电站为在建的最大高坝工程,工程泄洪消能采用“分散泄洪,分区消能”的原则,除了在坝身布置表深孔泄洪外,在左岸布置3条无压泄洪洞(图5),泄洪洞总设计流量达12 000 m3/s,占枢纽总泄洪能力的30%。泄洪洞下游出口位于距离电站下游2.7 km的白鹤滩滩地,利用白鹤滩村宽阔的I级阶地(宽约200 m)消能。3条泄洪洞并列布置,沿河道方向依次为3#、2#及1#泄洪洞出口,出口间距约63 m,采用挑流消能,消能区护坡不护底。泄洪洞消能区河道上游布置有坝身、电站等泄水建筑物,最小流量可小于600 m3/s,最大可能超过20 000 m3/s,上游流量直接影响泄洪洞消能区河道水位及流速,同时泄洪洞泄洪水流相互影响,河道冲刷问题复杂。
对河道冲刷的研究基于白鹤滩1∶50整体水工模型。整体模型根据重力相似准则设计,模型包括枢纽主要泄洪建筑物、电站及下游河道,主要过水建筑物均由有机玻璃制作;下游过水河道采用水泥抹面制作,并根据现场河道实测资料适当加糙以满足河道糙率相似;泄洪洞出口消能区采用动床模拟,在充分考虑河道水力条件和试验需求的基础上,选取动床模拟范围为泄洪洞出口上游300 m,下游700 m。根据地形资料制作河道开挖断面,白鹤滩台地覆盖层主要为碎石混合土及卵、砾石组合而成,根据白鹤滩台地的颗分试验结果,白鹤滩台地覆盖层主要为20~200 mm的碎石,质量占比为50%~60%,其次为2~20 mm的砾石,质量占比为30%~40%。根据夏毓常[16]的计算方法,估算原型覆盖层的主要成分抗冲流速为5~7 m/s,经综合考虑,试验采用多种粒径块石按照原型比例混合作为模型覆盖层,模型散粒体采用中值粒径为0.8 cm砂砾配以中值粒径2.3 cm碎石混合模拟,模型散粒体的主要成分抗冲流速相当于原型值5~7 m/s,基本可以满足冲刷模拟的要求。本文取散粒体平均抗冲流速为6 m/s。
白鹤滩水电站岸边泄洪洞运行时,若考虑上游电站满发,则泄洪洞上游来流量约为8 765 m3/s,根据下游水位不同,泄洪洞出口处河道平均流速为1.8~3.3 m/s。当多个泄洪洞联合运行时,在河道中泄洪水舌落水点形成冲坑。试验过程中可以观察到,当多个泄洪洞联合运行时,下游泄洪洞形成的冲坑比上游冲坑略浅。为深入研究河道流速对泄洪冲刷的影响,设计了两组试验工况(表1),唯一的差别在于消能区河道上游是否有额外流量。
表 1 试验工况Table 1. Model test conditions工况编号 工况描述 上游水位/m 下游水位/m 上游来流量/(m3·s−1) 泄洪洞流量/(m3·s−1) 鼻坎单宽流量/(m2·s−1) 1 1#+3# 785 597.3 0 1 370 66.8 2 1#+3# 785 597.3 8 765 1 370 66.8 试验过程中测量水舌的入水参数,根据测量结果使用本文提出的方法计算冲坑深度。由于采用了扭曲型鼻坎体型,射流在空中扩散较为明显,水舌入水时单宽流量已有大幅降低。试验过程中测量射流水舌的入水宽度
$ s $ ,根据入水宽度计算水舌入水单宽流量;根据水舌轨迹计算与试验观测,水舌入水角度范围为50°~60°,计算时取$ \alpha $ =55°;水舌入水流速按照v0=η$\sqrt {2gH} $ 计算,其中$ H $ 为包括鼻坎至下游水面的总水头,$ \eta $ 为考虑水流入水分散的流速折减系数,结合试验中对水舌入水范围内平均流速的测量结果,取$ \eta = 0.5 $ ;相应的水舌入水厚度按照$ {d_0} = {q_i}/{v_0} $ 取值。作为对比,按照目前使用最广泛的陈椿庭公式计算冲刷深度,即
$ T = {K_{\text{r}}}{q^m}{H^n} $ ,其中T为冲坑处最大水深,m、n为指数,一般取m=0.5,n=0.25,$ {K_{\text{r}}} $ 为综合冲刷系数,根据文献[16]推荐的计算方法取值,即${K_{\text{r}}} = 2.71V^{ - 0.3}_{ {\rm{k}}} $ (式中Vk为散粒体抗冲流速)。陈氏公式计算结果、本文方法计算结果及试验结果见表2。由于陈氏公式并未考虑河道流速,故两个工况下各泄洪洞的预测冲坑深度相同,但工况2形成的冲坑深度明显小于工况1,且位于上游的3#泄洪洞对应的冲坑深度均大于远离上游的1#泄洪洞的冲坑深度(见图6)。分析认为由于上游河道的来流导致泄洪消能区河道水流由静水变为动水,从而削弱了下游泄洪洞的冲刷;受到上游3#泄洪洞泄洪流量的影响,1#泄洪洞水舌落点附近河道流速进一步增加,故河道冲刷进一步减轻。本文方法计算结果与试验数据较为接近。表 2 计算结果与试验结果对比Table 2. Calculated results compared with experimental results工况编号 上游来流量/
(m3·s−1)泄洪洞流量/
(m3·s−1)陈氏公式计算冲坑深度/m 3#泄洪洞冲坑深度/m 1#泄洪洞冲坑深度/m 计算值 试验值 计算值 试验值 1 0 1 370 34.4 35.8 36.8 33.6 31.2 2 8765 1 370 34.4 29.6 29.9 27.9 26.8 为进一步验证计算方法的合理性,选取多个不同上下游水位及泄洪洞运行组合,并将河道上游来流量为电站满发流量8 765 m3/s作为试验工况,计算了3#泄洪洞及其相邻的2#泄洪洞联合运行形成的河道冲坑深度。根据泄洪消能区水位不同,3#泄洪洞水舌落水点附近河道流速为1.9~2.7 m/s。受到3#泄洪洞流量的影响,位于其下游的2#泄洪洞落水点附近河道流速略有增加。结合水舌入水相关参数计算了河道冲坑深度,并与试验值进行对比(表3)。从试验结果可以看出,在不同运行工况下,位于下游侧的2#泄洪洞冲坑深度均小于位于其上游的3#泄洪洞冲坑深度,根据工况不同,两者差值范围为1.7~5.0 m;各工况下的计算值与试验值较为接近,2#泄洪洞冲坑深度计算值均略小于3#泄洪洞冲坑深度计算值。各工况下相邻泄洪洞冲坑深度的计算值与试验值误差大多小于10%。考虑到试验冲坑深度与颗粒级配、铺砂均匀程度等多个因素有关,可以认为本文分析方法合理。
表 3 泄洪洞下游冲刷试验结果Table 3. Model test results of scouring downstream of the spillway tunnels上游
水位/m下游
水位/m3#泄洪洞落水点
河道流速/(m·s−1)3#泄洪洞冲坑深度 2#泄洪洞落水点
河道流速/(m·s−1)2#泄洪洞冲坑深度 冲坑深度差值 计算值/
m试验值/
m相对
误差%计算值/
m试验值/
m相对
误差%计算值/
m试验值/
m795 599.9 2.7 31.9 33.3 −4% 3.2 29.6 31.6 −6% 2.3 1.7 795 604.0 2.2 45.4 45.1 1% 2.6 43.6 42.2 3% 1.8 2.9 800 600.6 2.7 33.7 38.5 −12% 3.3 32.0 34.2 −6% 1.7 4.3 800 605.4 2.1 48.9 49.2 −1% 2.7 46.0 44.2 4% 2.9 5.0 810 601.8 2.5 43.9 44.5 −1% 3.1 40.8 39.8 3% 3.1 4.7 810 607.2 1.9 52.0 51.0 2% 2.6 50.0 48.1 4% 2.0 2.9 825 602.9 2.3 44.9 46.7 −4% 3.1 40.6 44.3 −8% 4.3 2.4 3. 结 语
根据冲击射流的相关理论,推导了射流入水后扩散流程与时间的关系式,分析了动水中的射流扩散形态,研究了河道水流流速对射流流速衰减的影响。将研究结果应用于白鹤滩水电站岸边泄洪洞下游河道的冲刷预测,计算了不同河道流速与泄洪洞运行组合下的冲坑深度。考虑河道动水流速的因素能较好地解释并联泄洪洞不同位置的冲坑深度差异,不同位置冲坑深度的计算结果与试验结果吻合较好,相对误差大多在10%以下。相对于以往的冲坑预测公式,本文方法更加适用于岸边式泄洪洞的冲坑预测。
-
表 1 试验工况
Table 1 Model test conditions
工况编号 工况描述 上游水位/m 下游水位/m 上游来流量/(m3·s−1) 泄洪洞流量/(m3·s−1) 鼻坎单宽流量/(m2·s−1) 1 1#+3# 785 597.3 0 1 370 66.8 2 1#+3# 785 597.3 8 765 1 370 66.8 表 2 计算结果与试验结果对比
Table 2 Calculated results compared with experimental results
工况编号 上游来流量/
(m3·s−1)泄洪洞流量/
(m3·s−1)陈氏公式计算冲坑深度/m 3#泄洪洞冲坑深度/m 1#泄洪洞冲坑深度/m 计算值 试验值 计算值 试验值 1 0 1 370 34.4 35.8 36.8 33.6 31.2 2 8765 1 370 34.4 29.6 29.9 27.9 26.8 表 3 泄洪洞下游冲刷试验结果
Table 3 Model test results of scouring downstream of the spillway tunnels
上游
水位/m下游
水位/m3#泄洪洞落水点
河道流速/(m·s−1)3#泄洪洞冲坑深度 2#泄洪洞落水点
河道流速/(m·s−1)2#泄洪洞冲坑深度 冲坑深度差值 计算值/
m试验值/
m相对
误差%计算值/
m试验值/
m相对
误差%计算值/
m试验值/
m795 599.9 2.7 31.9 33.3 −4% 3.2 29.6 31.6 −6% 2.3 1.7 795 604.0 2.2 45.4 45.1 1% 2.6 43.6 42.2 3% 1.8 2.9 800 600.6 2.7 33.7 38.5 −12% 3.3 32.0 34.2 −6% 1.7 4.3 800 605.4 2.1 48.9 49.2 −1% 2.7 46.0 44.2 4% 2.9 5.0 810 601.8 2.5 43.9 44.5 −1% 3.1 40.8 39.8 3% 3.1 4.7 810 607.2 1.9 52.0 51.0 2% 2.6 50.0 48.1 4% 2.0 2.9 825 602.9 2.3 44.9 46.7 −4% 3.1 40.6 44.3 −8% 4.3 2.4 -
[1] CALITZ J. Analysis of the hydrodynamics of rectangular plunging jets and the subsequent scouring in broken-up rock beds[D]. Stellenbosch: Stellenbosch University, 2016.
[2] MALEKI S, FIOROTTO V. Blocks stability in plunge pools under turbulent rectangular jets[J]. Journal of Hydraulic Engineering, 2019, 145(4): 04019007. doi: 10.1061/(ASCE)HY.1943-7900.0001573
[3] DUARTE R, PINHEIRO A, SCHLEISS A J. An enhanced physically based scour model for considering jet air entrainment[J]. Engineering, 2016, 2(3): 294-301. doi: 10.1016/J.ENG.2016.03.003
[4] BOLLAERT E F R, SCHLEISS A J. Physically based model for evaluation of rock scour due to high-velocity jet impact[J]. Journal of Hydraulic Engineering, 2005, 131(3): 153-165. doi: 10.1061/(ASCE)0733-9429(2005)131:3(153)
[5] BOLLAERT E F R. Physics of rock scour: the power of the bubble[C]∥Scour and Erosion. Reston: American Society of Civil Engineers, 2010.
[6] BOLLAERT E. A comprehensive model to evaluate scour formation in plunge pools[J]. International Journal on Hydropower & Dams, 2004, 23(1): 94-101.
[7] SCHMOCKER L, PFISTER M, HAGER W H, et al. Aeration characteristics of ski jump jets[J]. Journal of Hydraulic Engineering, 2008, 134(1): 90-97. doi: 10.1061/(ASCE)0733-9429(2008)134:1(90)
[8] 孙建, 李玉柱, 余常昭. 小湾工程护坡不护底水垫塘的试验研究[J]. 水利水电技术,2001,32(5):52-56 doi: 10.3969/j.issn.1000-0860.2001.05.015 SUN Jian, LI Yuzhu, YU Changzhao. Experimental research on the cushion pool with lining slope but no bottom protection in Xiaowan project[J]. Water Resources and Hydropower Engineering, 2001, 32(5): 52-56. (in Chinese) doi: 10.3969/j.issn.1000-0860.2001.05.015
[9] 冬俊瑞, 黄继汤, 徐一春, 等. 三峡水利枢纽溢流坝挑流基岩冲刷研究[J]. 长江科学院院报,1991,8(2):10-21 DONG Junrui, HUANG Jitang, XU Yichun, et al. Study on the scour of the rockbed by plunging jet downstream of the Three Gorges spillway[J]. Journal of Yangtze River Scientific Research Institute, 1991, 8(2): 10-21. (in Chinese)
[10] 郭振仁, 蒋伟强, 彭海君. 流速和水深对射流扩散的影响[J]. 环境科学研究,1990(6):57-62 doi: 10.3321/j.issn:1001-6929.1990.06.012 GUO Zhenren, JIANG Weiqiang, PENG Haijun. Effections of current and depth on dilution of immerged jets[J]. Research of Environmental Sciences, 1990(6): 57-62. (in Chinese) doi: 10.3321/j.issn:1001-6929.1990.06.012
[11] 罗铭, 郭亚昆. 有界二元掺气射流水下扩散规律研究[J]. 水利学报,1992(7):29-34 doi: 10.3321/j.issn:0559-9350.1992.07.005 LUO Ming, GUO Yakun. Study on underwater spread of binary aerated jet[J]. Journal of Hydraulic Engineering, 1992(7): 29-34. (in Chinese) doi: 10.3321/j.issn:0559-9350.1992.07.005
[12] 辜晋德, 赵建钧, 安建峰. 挑流水垫塘掺气比尺效应试验[J]. 水利水电科技进展,2019,39(2):61-65 GU Jinde, ZHAO Jianjun, AN Jianfeng. Experimental study on scale effect of a aerated jet in a plunge pool[J]. Advances in Science and Technology of Water Resources, 2019, 39(2): 61-65. (in Chinese)
[13] 刘沛清, 高季章, 李永梅. 多层水股射流在水垫塘内的流动特征与动水垫效应分析[J]. 水利学报,1999,30(3):1-7 doi: 10.3321/j.issn:0559-9350.1999.03.001 LIU Peiqing, GAO Jizhang, LI Yongmei. Flow characteristics of multi jet impinged into a plunge pool and the effect of flowing water cushion[J]. Journal of Hydraulic Engineering, 1999, 30(3): 1-7. (in Chinese) doi: 10.3321/j.issn:0559-9350.1999.03.001
[14] 焦爱萍, 刘沛清, 刘宪亮, 等. 多层水股射流入射水垫塘流场特性的优化分析[J]. 水力发电学报,2008,27(1):48-52 doi: 10.3969/j.issn.1003-1243.2008.01.010 JIAO Aiping, LIU Peiqing, LIU Xianliang, et al. Optimum analysis on flow field characteristics of multi-jet impinging into a plunge pool[J]. Journal of Hydroelectric Engineering, 2008, 27(1): 48-52. (in Chinese) doi: 10.3969/j.issn.1003-1243.2008.01.010
[15] ALBERTSON M L, DAI Y B, JENSEN R A, et al. Diffusion of submerged jets[J]. Transactions of the American Society of Civil Engineers, 1950, 115(1): 639-664. doi: 10.1061/TACEAT.0006302
[16] 夏毓常. 岩基挑流冲刷原型观测与模型试验比较分析[J]. 长江科学院院报,1996,13(4):6-10 XIA Yuchang. Comparative analysis on prototype observation and model test results of jet scour in rock foundation[J]. Journal of Yangtze River Scientific Research Institute, 1996, 13(4): 6-10. (in Chinese)



 Email Alerts
Email Alerts RSS
RSS
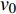
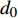
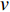
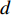
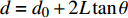
 下载:
下载: