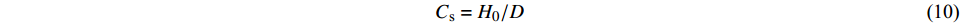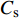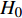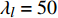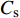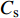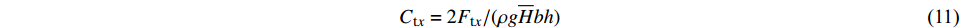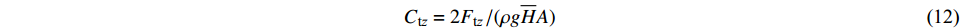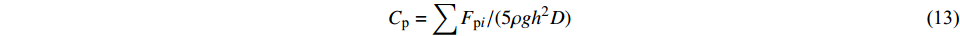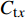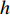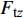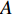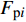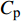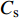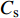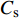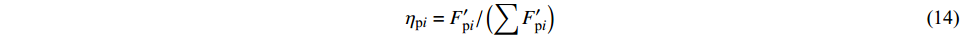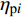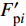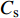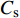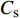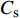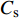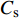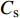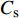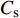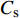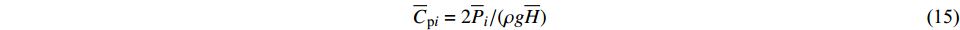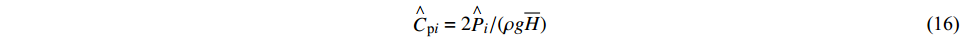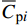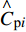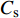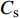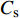Numerical simulation of wave-current load on high pile cap foundation
-
摘要: 为研究高桩承台基础在波流作用下的荷载时程特点和压力分布规律,开展某跨海大桥桩-承台复合基础的数值模拟研究。根据Stokes二阶波理论进行数值水池造波,采用雷诺平均应力方程(RANS)求解流体运动方程,计算得出3种淹没系数(0~1)下高桩承台基础的各部分水动力时程及其表面压力分布;应用流体体积函数(VOF)追踪液面形态模拟波浪形态时程。研究结果表明:(1)淹没系数较大时,承台水平力较大且主要来自波流联合作用,尾流区绕射波浪会产生负向水平力和负向浮托力,承台迎波面及顶面后方存在压力波动极值区;(2)随着淹没系数的降低,承台水平力减小,水平力主要以波浪拍击力为主,竖向浮托力、单桩水平力随之增加,尾流区绕射效应降低,承台压力极值波动区缩小直至消失;(3)桩基正向水平力最大值出现在边列最后排桩;负向水平力最大值出现在中列最后排桩。研究所得总力时程和压力分布规律可为优化结构设计提供参考。Abstract: In order to study the load time history characteristics and pressure distribution law of high pile cap foundation under wave current, the pile cap composite foundation of a sea crossing bridge is numerically simulated. According to Stokes second-order wave theory, wave generation in numerical pool is carried out, and Reynolds averaged Navier stokes equation (RANS) is used to solve the fluid motion equation. The hydrodynamic time history and surface pressure distribution of each part of high pile cap foundation under three submergence coefficients in the range of 0~1 are calculated. The volume of fluid function (VOF) is used to track the liquid surface shape and simulate the wave shape time history. The results show that: (1) When the submergence coefficient is large, the horizontal force of the cushion cap is large and mainly comes from the combined action of wave and current; the diffracted waves in the wake area will produce negative horizontal force and negative buoyancy force; there is an extreme pressure fluctuation region on the upstream and downstream of the cushion cap. (2) With the decrease of submergence coefficient, the horizontal force of cushion cap decreases, and the horizontal force is mainly wave beating force; the vertical buoyancy force and the horizontal force of single pile increase accordingly; the diffraction effect in the wake region is reduced; the fluctuation area of extreme pressure of bearing platform is reduced until it disappears. (3) The maximum positive horizontal force of the pile foundation appears in the last row of piles on the side column; the maximum negative horizontal force appears in the last row of piles in the middle column. The research on the total force history and pressure distribution law can provide a reference for optimizing structural design.
-
Keywords:
- wave current force /
- high pile cap /
- time history analysis /
- pressure distribution
-
跨海桥梁处于海洋环境中,浪、流荷载是其重要的控制荷载。海洋环境多变复杂,近海地区台风、巨浪等极端气候多有发生。历史上曾多次发生飓风引发极端浪潮对桥梁结构造成严重破坏的事故[1]。跨海大桥的桥墩、承台及桩基础长期受到波浪及水流荷载冲击,受力复杂[2-3]。因此,深入研究波流对桥梁基础的荷载作用具有重要的理论意义和工程价值。工程实践中,目前中、美、英等国的规范均采用基于Morison小尺度水工结构水平力计算公式[4]。Morison方程是一个半经验、半解析的简化计算式,当特征尺寸与入射波长之比小于0.2时,计算精度基本满足工程需要[5]。对于大尺度结构,由于构筑物与波浪场的相互耦合干扰,会产生复杂的绕射、反射效应,采用Morison方程计算波浪力往往会高估结构所受的荷载[6]。跨海大桥桥墩、基础等属于典型的大尺度构筑物。针对大尺度构筑物波浪力的研究,Maccamy等[7]基于势流理论首先提出了线性绕射理论计算大尺度圆柱波浪力,后人不断对势流理论和绕射理论进行补充和完善[8-11]。物理水槽试验是研究水动力学的重要手段,兰雅梅[12]采用水槽试验方法对规则波作用于承台及单桩的水动力特性开展研究,得到了冲击压强随承台相对净空及相对长度的变化规律,讨论了承台对桩柱的水动力影响;魏凯等[13]进行了极端波浪冲击高桩承台的水槽试验,基于试验数据建立了波浪冲击荷载时程模型,并基于Copula理论,建立了荷载上升段和峰值段的联合概率模型。随着计算机技术和计算流体力学(CFD)理论的发展,数值模拟试验被广泛应用于波流荷载的研究。仇正中等[14]基于三维势流理论,采用流体动力学软件SESAM,对某大桥主桥墩承台基础波浪荷载展开研究,计算不同波浪周期、承台吃水、浪向角情况下的承台荷载,分析承台波浪荷载的变化规律,研究认为实际施工中承台吃水和波浪荷载近似呈线性关系,需考虑约15%的安全系数;刘正浩等[15]应用自主研发的CFD求解器,对不同水深工况下的固定式高桩承台风机基础的水动力参数进行数值模拟,研究发现水深对风机基础水平向的受力影响不大,但对砰击压力的影响很大,水深越深,风机基础受到的砰击压力越大,波高对风机基础的受力影响很大,波高越大,观察到的波浪破碎现象越严重。
多数学者的研究对象聚焦于桥梁基础在波浪作用下的整体受力趋势[16-19],而对其表面的压力分布关注较少。掌握承台-桩基表面压力分布规律,可以优化结构设计。另外,桥梁基础波浪荷载来自于波浪的冲击惯性力及流体压差,波浪和结构相互作用时,一般将结构视为刚体模型,而波浪冲击结构时,波浪会产生越浪、绕射等效应,扭曲变形的波浪反作用于结构。因此,结合波浪荷载时程,研究波浪与结构相互作用时形态变化有助于更全面深入地了解波浪荷载的形成机理。然而,解析计算方法仅适用于规则的桩柱结构,物理水槽试验方法能够较为客观地反映结构整体受力情况,但限于测点布置数量及布置测点本身对结构表面的影响,使得物理试验很难完整真实地描述复杂结构的表面压力分布。同时,试验方法也不便于追踪和记录水质点的即时波高。数值模拟方法可以很好地描述复杂桥梁基础的表面压力分布,能够记录波浪场中任意时刻任意质点的即时波高,进而描述波浪冲击基础时的形态变化。
基于上述分析,拟开展某跨海大桥高桩承台复合基础的波流荷载数值模拟。首先,通过网格比选进行模拟试算,将计算所得水动力参数与已有物理水槽试验数据进行对比,验证数值模拟的准确性;然后改变初始静水面标高,计算不同淹没系数下的高桩承台复合基础的水平力、浮托力;进一步研究典型周期内波流冲击复合基础各阶段的波浪形态,分析讨论承台及桩基的压力分布规律。
1. 控制方程及数值水池造波方法
1.1 RANS法控制方程
采用不可压缩流体运动的三维雷诺时均方程,RANS法的连续方程为:
$$ {{\partial u}}/{{\partial x}} + {{\partial v}}/{{\partial y}} + {{\partial w}}/{{\partial {\textit{z}}}} = 0 $$ (1) 式中:
$ u $ 、$ v $ 、$ w $ 分别为流体在x、y、z方向的速度(m/s)。考虑到出口处波浪反射会对计算域内流场产生干扰,故在出口1~2倍波长范围内设置消波区。采用源项消波方法,在消波区范围内设置阻尼消波项。添加消波源项后的动量方程如下:
$$ {\partial {u}_{i}}/{\partial t}+{u}_{j}{\partial {u}_{i}}/{\partial {x}_{j}}=(-{1}/{\rho }){\partial p}/{\partial {x}_{i}}+{g}_{\text{z}}+{\partial }\left(\upsilon {\partial {u}_{i}}/{\partial {x}_{j}}-\overline{{{u}}'_{i}{{u}}'_{j}}\right)/{\partial {x}_{j}}-\mu (x){u}_{i} $$ (2) $$ - \overline {{{u}'_i}{{u}'_j}} = {\nu _t}\left({{\partial {u_i}}}/{{\partial {x_j}}} + {{\partial {u_j}}}/{{\partial {x_i}}} \right)- {2}k{\delta _{ij}}/3 $$ (3) $$ \mu (x) = \alpha (x - {x_1})(x - {x_2}) $$ (4) 式中:
$ {u_i} $ 、$ {u_j} $ 为$ i $ 、$ j $ 坐标方向的流体运动时均化速度;t为时间;$\; \rho $ 为流体密度,取998 kg/m3;p为流体压强;$ {g_{\text{z}}} $ 为竖向重力加速度,取9.8 m/s2;$ \upsilon $ 为运动黏度,取1.006×10−6 m2/s;$ \overline {{{u}'_i}{{u}'_j}} $ 为雷诺时均应力;${\nu _t} = \rho {C_\mu }{{k^2}}/ {\varepsilon }$ 定义为湍流速度;δij为“Kronecker delta”符号,即当i=j时,δij=1;当i≠j时,δij=0;$ k $ 、$ \varepsilon $ 分别为湍动能和湍动能耗散率;$ \alpha $ 为消波经验系数;$ {x_1} $ 、$ {x_2} $ 分别为波流传播方向的消波区起始点和结束点的坐标值。1.2 数值水池造波方法
将速度及体积分数变化函数编写UDF语言并设置为入口的边界条件。根据Stokes波浪理论进行数值模拟造波。选用Stokes二阶波模型造波,其任意时刻的波面函数及势函数分别为:
$$ \eta = \frac{H}{2}\cos (kx - \omega t) + \frac{{{\text{π}}H}}{8}\left(\frac{H}{L}\right)\frac{{\cosh (kh)[\cos (2kh) + 2]}}{{{{\sinh }^3}(kh)}}\cos 2(kx - \omega t) $$ (5) $$ \phi = \frac{{{\text{π}}H}}{{kT}}\frac{{\cosh (k({\textit{z}} + h))}}{{\sinh (kh)}}\sin (kx - \omega t) + \frac{3}{8}\frac{{{{\text{π}}^2}H}}{{kT}}\left(\frac{H}{L}\right)\frac{{\cosh [2k({\textit{z}} + h)]}}{{{{\sinh }^4}(kh)}}\sin 2(kx - \omega t) $$ (6) 式中:
$ H $ 为波高;$ T $ 为周期;$ L $ 为波长;$ h $ 为水深;$ {\textit{z}} $ 为即时波高;$ k = 2{\text{π}}/L $ ,$ \omega = 2{\text{π}}/{{T}} $ 。对势函数求导即可得到水平向和竖向的波浪传播速度:
$$ u = \frac{{\partial \phi }}{{\partial x}} = \frac{{{\text{π}}H}}{T}\frac{{\cosh [k(h + {\textit{z}})]}}{{\sinh (kh)}}\cos (kx - \omega t) + \frac{3}{4}\frac{{{{\text{π}}^2}H}}{T}\left(\frac{H}{L}\right)\frac{{\cosh [2k({\textit{z}} + h)]}}{{{{\sinh }^4}(kh)}}\cos 2(kx - \omega t) $$ (7) $$ w = \frac{{\partial \phi }}{{\partial {\textit{z}}}} = \frac{{{\text{π}}H}}{T}\frac{{\sinh [k(h + {\textit{z}})]}}{{\sinh (kh)}}\sin (kx - \omega t) + \frac{3}{4}\frac{{{{\text{π}}^2}H}}{T}\left(\frac{H}{L}\right)\frac{{\sinh [2k({\textit{z}} + h)]}}{{{{\sinh }^4}(kh)}}\sin 2(kx - \omega t) $$ (8) 采用VOF方法对液面变化进行模拟跟踪。其主要思路是:假设每个控制体积多相体积分数总和为1,每个控制容积第一相体积含量为
$ {a_q} $ ,若$ {a_q} = 1 $ ,表示控制体积内只含有第一相,若$ {a_q} = 0 $ ,表示控制体积内不含第一相,若$ 0 < {a_q} < 1 $ ,则表示该控制容积包含多相流交界面。其显式时间离散格式的差分方程为:$$ \frac{{a_{q,{n + 1}}\rho _{q,{n + 1}} - a_{q,n}\rho _{q,n}}}{{\Delta t}}V + \sum\limits_f {({\rho _q}U_{f,n}a_{{qf},n})} = \left[\sum\limits_{p = 1}^n {({{\mathop m\limits^. }_{pq}} - {{\mathop m\limits^. }_{qp}}) + {S_{aq}}} \right]V $$ (9) 式中:n为当前计算时间步;
$\;\rho _{q}^{}$ 为第q相的物理密度;${\mathop m\limits^. }_{pq}$ 表示从第p相到q相的传质;$ {S_{aq}} $ 为源项;V为单元体积;$ U_f^{} $ 为通过单元截面的体积通量;$ a_{qf}^{} $ 为第q相体积分数的单元界面值。$\displaystyle\sum_{f}\left(\rho_{q} U_{f}^{n} a_{q f}^{n}\right)$ 表示控制体的净通量,即通过各个单元面法向方向的质量通量之和。2. 模型建立及验证
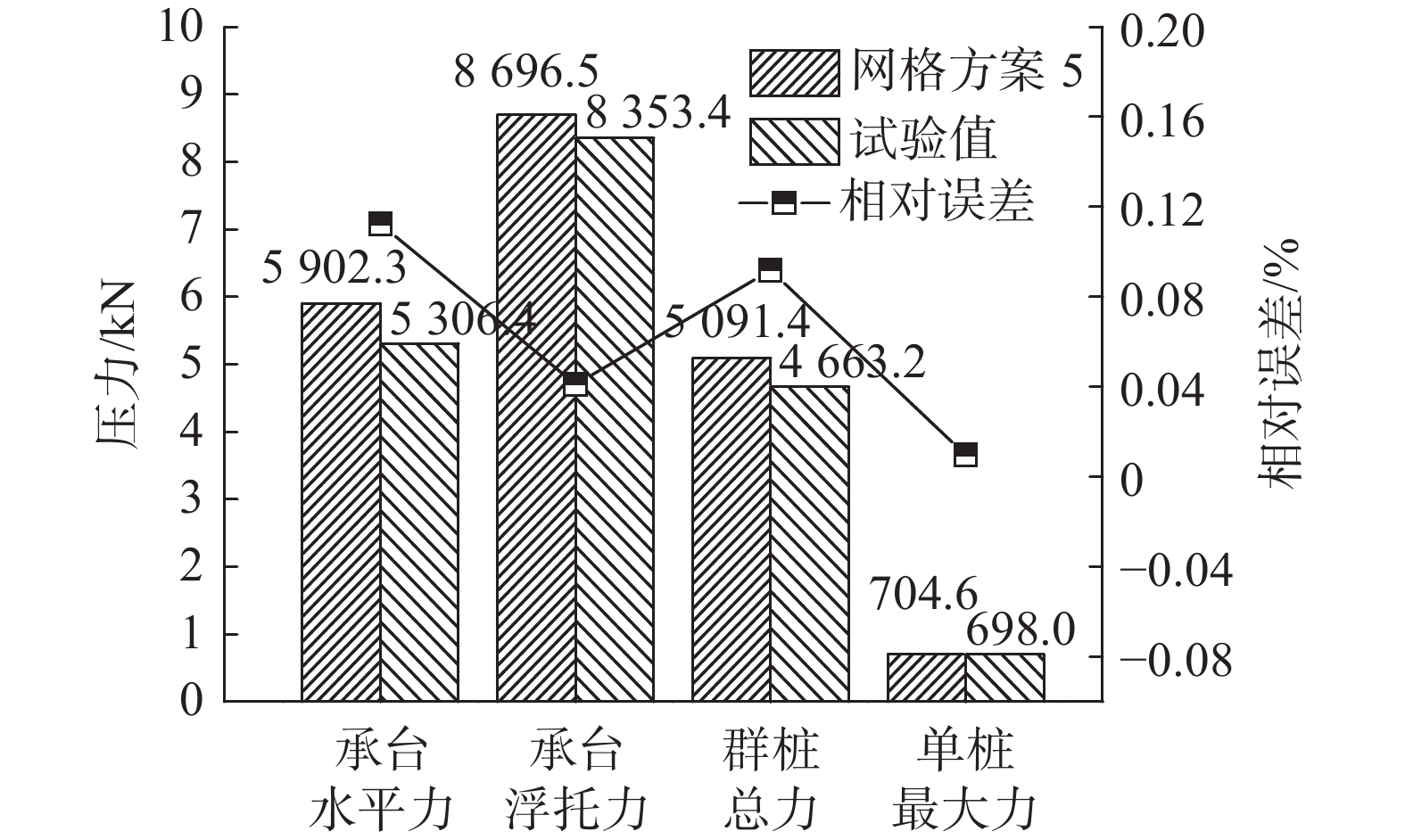
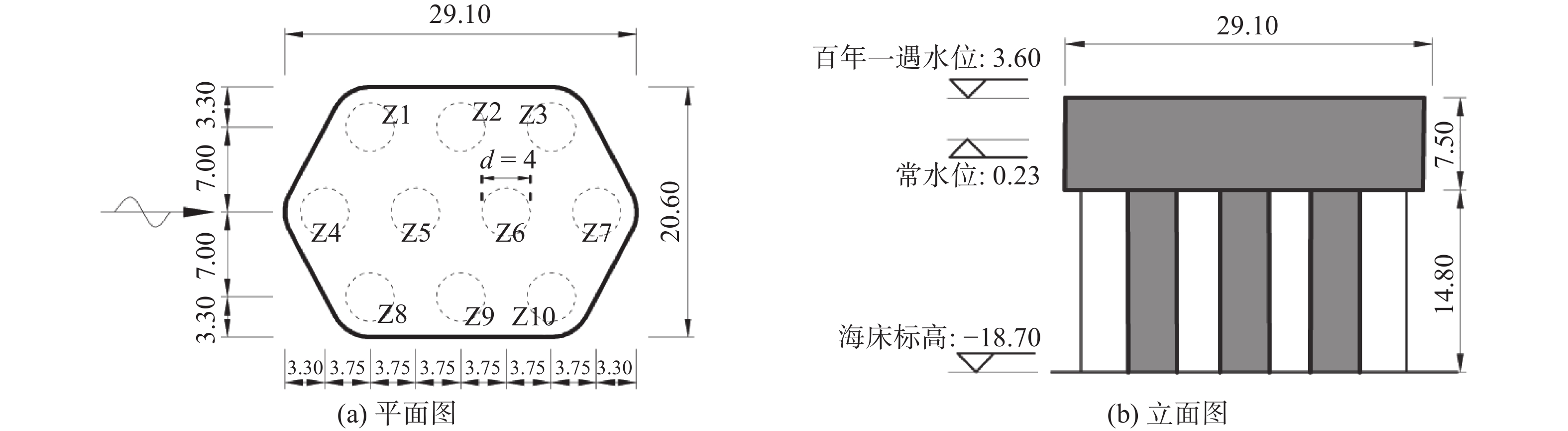
以某跨海大桥主桥墩承台-桩基础为研究对象,该桥墩基础为10桩配6棱承台结构形式,其具体尺寸见图1。为方便表示不同水位高度条件,定义无量纲承台淹没系数:
$$ {C_{\text{s}}} = {{{H_0}}}/{D} $$ (10) 式中:
$ {C_{\text{s}}} $ 为承台淹没系数;$ {H_0} $ 为静水面至承台下表面垂直高度(m);$ D $ 为承台厚度(m)。根据淹没系数,分别定义百年一遇水位、常年平均水位及静水面与承台底齐平时对应水位的3种工况,如图1(b)所示。波浪要素及工况条件如表1所示。
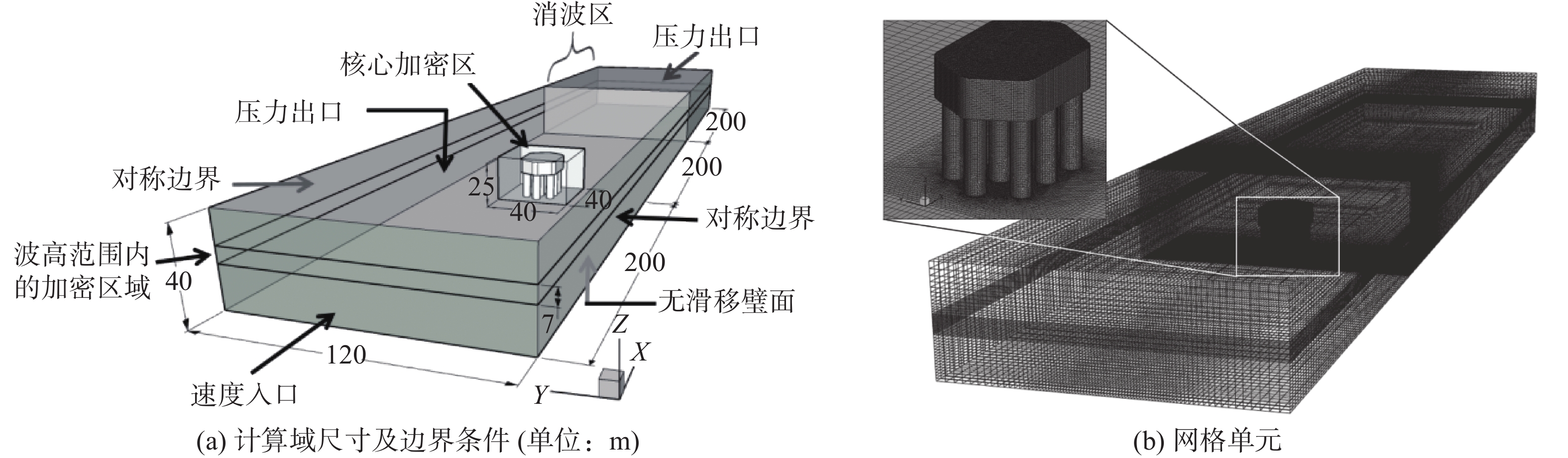
表 1 波浪要素及计算工况Table 1. Wave elements and working conditions淹没系数 静水深度/m 波高/m 周期/s 波长/m 静水流速/(m·s−1) Cs=1.00 22.30 6.9 8.3 96 3.64 Cs=0.55 18.93 Cs=0 14.80 为保证模拟计算准确性,需进行网格无关性检验。计算域范围:长度取近似6倍波长600 m,高度取40 m;宽度取120 m。在出口前2倍波长处设置消波区。桥墩底面中心设置在距入口处约2倍波长(200 m)处。整体计算域采用混合网格单元,约1个波高范围内(7 m)网格加密,布置20个单元,高0.35 m。在桥墩附近采用局部加密的非结构化网格,尺寸为40 m×40 m×25 m,桥墩表面网格加密。加密区以外计算域采用结构化网格,控制入口处最大网格尺寸,入口至加密区网格均匀分布。由于消波区至出口处不是重点考察对象,故出口处网格尺寸适当加大,加密区至出口范围网格按指数率分布。采用
$ k{{ - }}\varepsilon $ realizable湍流计算模型,离散方程求解采用PISO格式。VOF方程采用显式差分格式求解,时间步长0.005 s,迭代计算过程库朗数控制在0.5以下。计算域、边界条件及网格划分见图2。为验证网格无关性,设计6组网格方案进行试算,网格尺寸如表2所示。表 2 不同网格方案参数Table 2. Parameters of different grid schemes方案 最大网格尺寸/m 单元数/个 Z/Y向网格 X向网格 承台-桩表面网格 网格方案1 4.0 6.0 4.00 172 785 网格方案2 2.0 6.0 2.00 297 177 网格方案3 2.0 6.0 1.00 346 513 网格方案4 1.0 3.0 0.50 1 015 335 网格方案5 1.0 3.0 0.25 2 005 582 网格方案6 0.5 1.0 0.10 5 402 545 以某物模缩尺水槽试验为参考[20],验证数值模拟合理性。试验水槽长50 m,宽7 m,高1.2 m。根据《波浪模型试验规程》,试验模型几何比尺为
$ {\lambda _l} = 50 $ ,根据弗劳德相似准则,流速、时间、压强比尺及总力比尺分别为7.07、7.07、50及125 000。试验中在承台顶安装4个总力仪,以同步测定竖向浮托力;在承台的侧端与末端各安装 1个总力仪,以测定承台及桩基在水平方向上纵向与横向的总力;在承台前端布置3个压强点,以测定承台迎水面水平压强;在承台底部布置4个压强点,以测定承台底部的压强;除桥墩完成整体测力外,还将桥墩的承台与桩基进行分割,保持桩基位置不变,承台略往上抬保证其不与桩基接触,以便单独测量桩基测点压强及水平总力。试验测点布置及试验过程如图3和4所示。
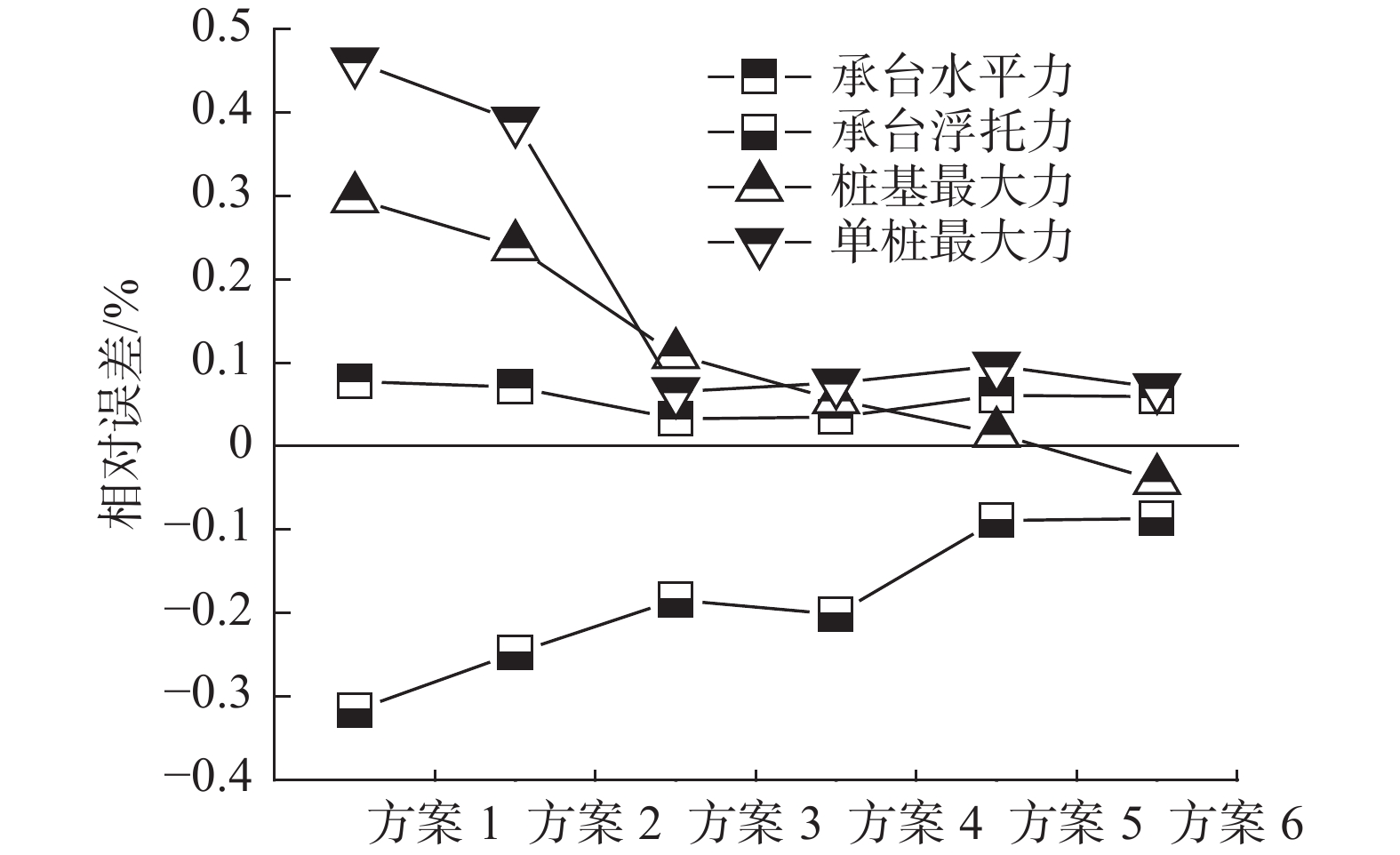
水槽试验测量及数值模拟计算结果见表3。由表3、图5可知,网格方案3~6的水平荷载计算值趋于一致,即水平向荷载对网格敏感性较低;而竖向浮托力对网格敏感性较高,当网格尺寸加密至方案5后,数值模拟结果基本收敛于试验值。分析说明采用网格方案5基本能达到数值模拟精度。
表 3$ {C_{\text{s}}} $ =1.00计算结果对比Table 3. Comparison of calculation results ($ {C_{\text{s}}} $ =1.00)单位:kN 方案 承台水平力 承台浮托力 桩基最大力 单桩最大力 网格方案1 7 296.22 3 154.68 5 698.01 741.48(Z8) 网格方案2 7 250.34 3 472.13 5 445.38 705.38(Z4) 网格方案3 6 993.28 3 766.94 4 876.31 540.78(Z10) 网格方案4 7 006.78 3 685.23 4 638.88 546.02(Z10) 网格方案5 7 182.15 4 206.10 4 461.20 556.40(Z3) 网格方案6 7 173.45 4 216.13 4 213.40 543.23(Z3) 试验数值 6 768.5 4 616.1 4 393.7 507.4(Z3) 为进一步验证网格方案选取的合理性和数值模拟的计算精度,利用网格方案5,仅改变波高加密区范围,计算
$ {C_{\text{s}}} $ =0.55工况对应的桩-承台表面压力。由图6可见,典型参数计算值的相对误差均控制在10%以内。综上可知,采用网格方案5能够兼顾计算效率和计算精度。3. 波流作用下桩-承台压力时程分析
为研究波流作用下的桩-承台压力时程特性,定义各压力荷载无量纲参数。承台水平力系数、承台浮托力系数及群桩总力系数分别定义如下:
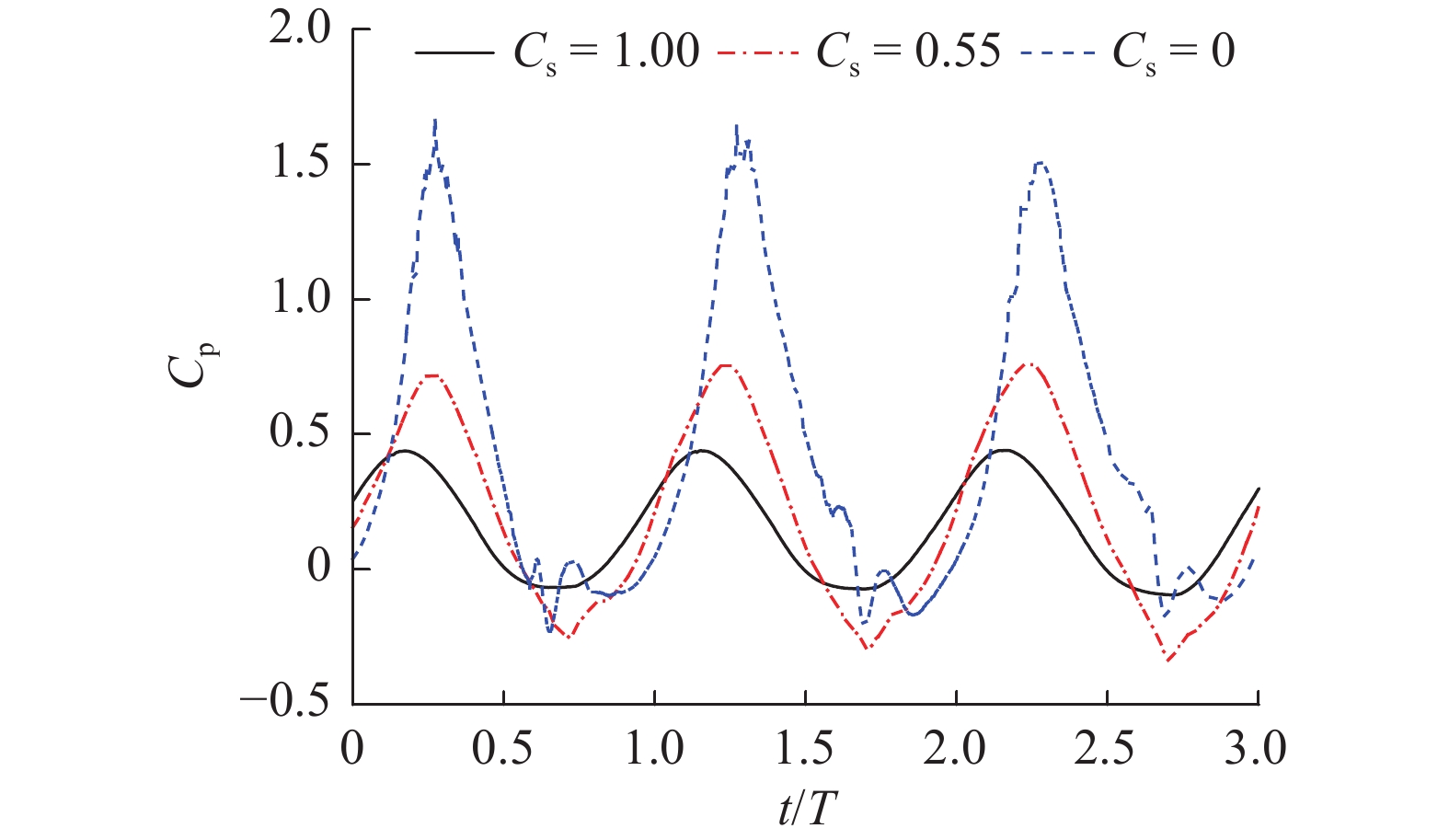
$$ {C_{{\text{t}}x}} = {{2{F_{{\text{t}}x}}}}/({{\rho g\overline H bh}}) $$ (11) $$ {C_{{\text{t}}{\textit{z}}}} = {{2{F_{{\text{t}}{\textit{z}}}}_{}}}/({{\rho g\overline H A}}) $$ (12) $$ {C_{\text{p}}} = {{\displaystyle\sum {{F_{{\text{p}}i}}} }}/({{5\rho g{h^2}D}}) $$ (13) 式中:
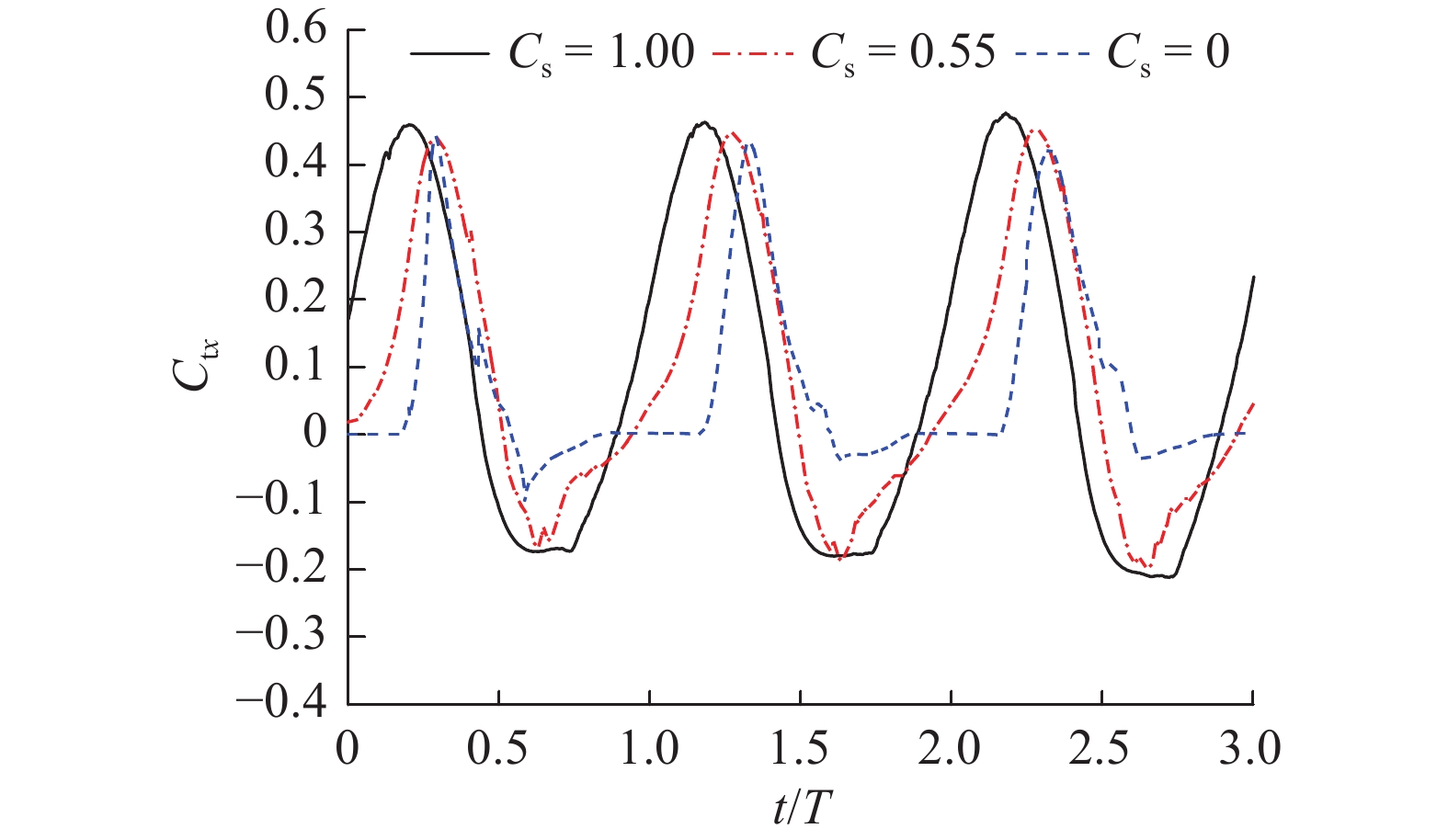
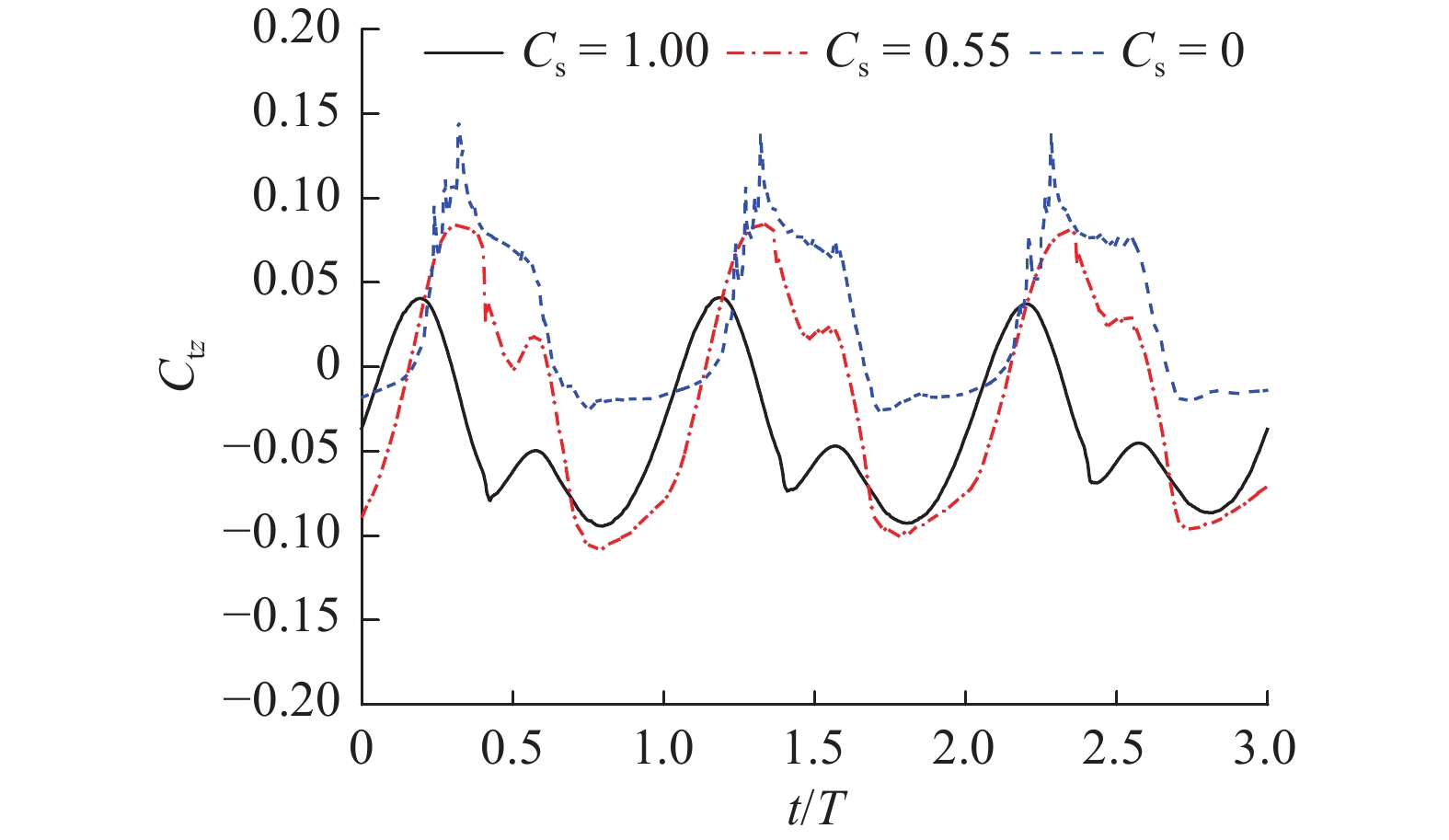
$ {C_{{\text{t}}x}} $ 为无量纲承台水平力系数;Ftx为承台所受波流水平力;$ \overline H $ 为波高;$ b $ 为承台宽;$ h $ 为水深;$ {C_{{\text{t}}{\textit{z}}}} $ 为无量纲承台浮托力系数;$ {F_{{\text{t}}{\textit{z}}}} $ 为承台所受波流浮托力;$ A $ 为承台底面积;$ {F_{{\text{p}}i}} $ 为单桩所受波流水平力;$ {C_{\text{p}}} $ 为群桩总力系数;$ D $ 为桩基直径。以上参数中下标含义:t为承台;p为桩基;x、z为荷载方向,分别表示沿波传播水平方向和竖直方向。图7、图8给出了3个完整周期内(t/T=1~3)承台水平压力系数和竖向浮托力系数的时程曲线。从图7可知,随着淹没系数的降低,正负向水平荷载也逐渐降低;峰值到达时间逐渐延后。当静水面处于承台底面以上时,正向荷载峰值过后产生明显的负向水平冲击力;而当淹没系数为零时,负向冲击效应逐渐减弱。图8显示了竖向浮托力的时程变化特征。与水平压力相反,随着淹没系数的降低,承台竖向浮托力随之增大,峰值到达时间同样延后。淹没系数大于0时,竖向浮托力在主峰值过后又产生1个次峰值,随着淹没系数减小至0,次峰值趋于平缓。当淹没系数为0时,可以观察到浮托力主峰值具有1~2次明显的脉冲效应,冲击时间短,冲击力强。浮托力峰值过后,反向浮托力冲击效应亦趋于平缓。
群桩总水平时程曲线如图9所示。与承台浮托力时程相似,随着淹没系数降低,群桩总力系数增大,且当
$ {C_{\text{s}}} $ =0时,群桩总力系数远大于承台淹没水中工况。由图9可知,群桩水平力总力系数的峰值过后,与$ {C_{\text{s}}} $ >0时曲线平稳下降有所不同,$ {C_{\text{s}}} $ =0时,在波谷附近产生明显的荷载波动。为考察在群桩总力最大状态下各单桩水平力分配情况,定义单桩贡献系数:
$$ {\eta _{{\text{p}}i}} = {{{{F}'_{{\text{p}}i}}}}/\left({{\displaystyle\sum {{{F}'_{{\text{p}}i}}} }}\right) $$ (14) 式中:
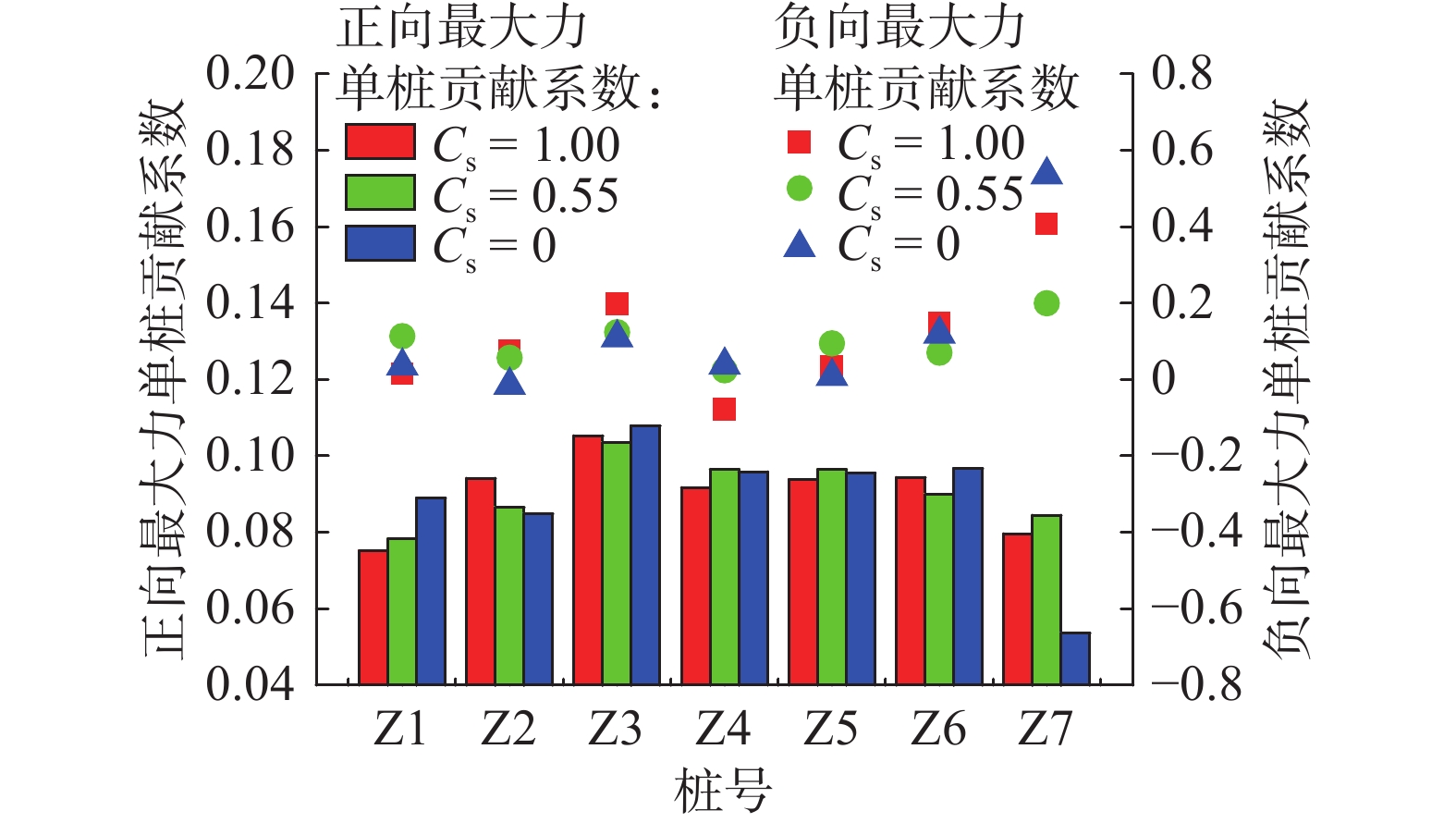
$ {\eta _{{\text{p}}i}} $ 为无量纲单桩贡献系数;$ {F'_{{\text{p}}i}} $ 为群桩总力达到最大值时各单桩水平力值;$ \displaystyle\sum {{{F}'_{{\text{p}}i}}} $ 为某周期内群桩正向、负向群桩总力最大值。下标i表示桩号。取典型周期(t/T=1~3)内的群桩总力时程进行分析,其正向、负向最大力下的各单桩贡献系数如图10所示。可见,在群桩正向总力达到最大值时,3种工况下的Z3(Z10)单桩贡献系数均最大,当
$ {C_{\text{s}}} $ =0时,Z1贡献系数增大,而Z7贡献系数则明显减小;当群桩负向总力达到最大值时,中间一排桩(Z4~Z7)存在明显的越靠后排贡献系数越大的规律,且Z7贡献系数明显大于其他位置桩,随着水位下降,其值明显增大。由此可见负向最大值主要来自于Z7承受的反向波流冲击。4. 波浪形态时程及波浪荷载形成机理
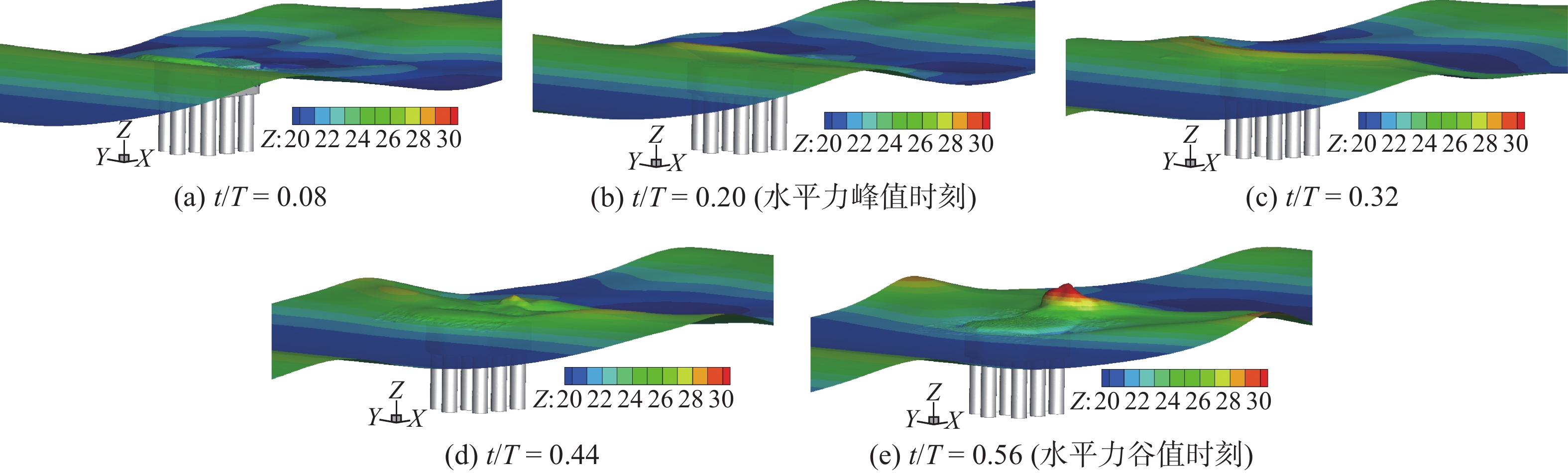
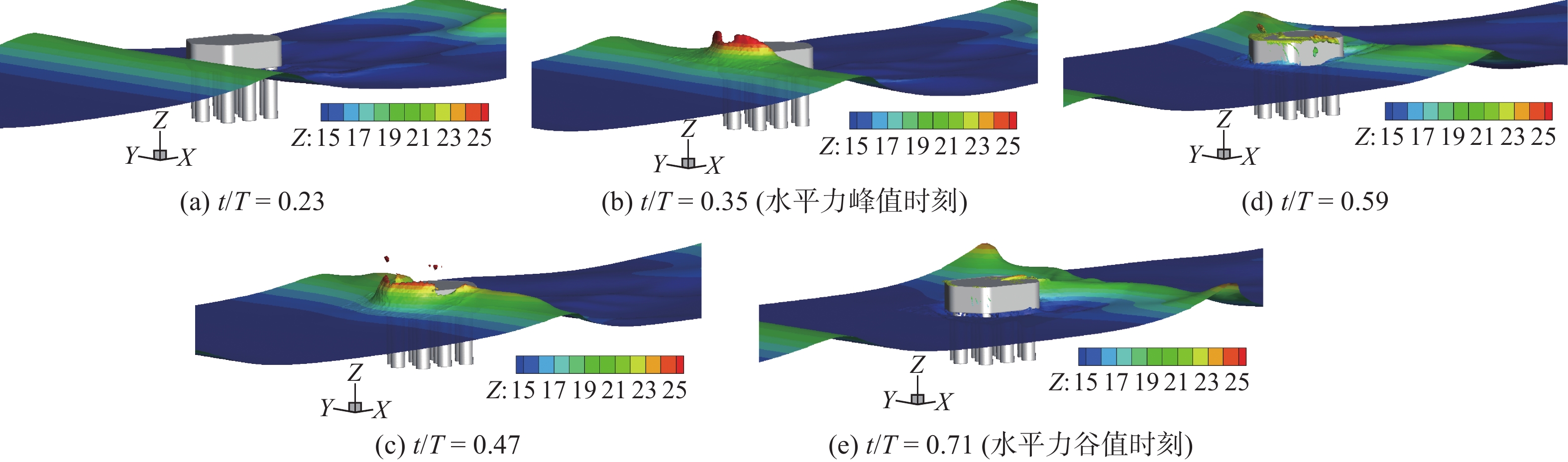
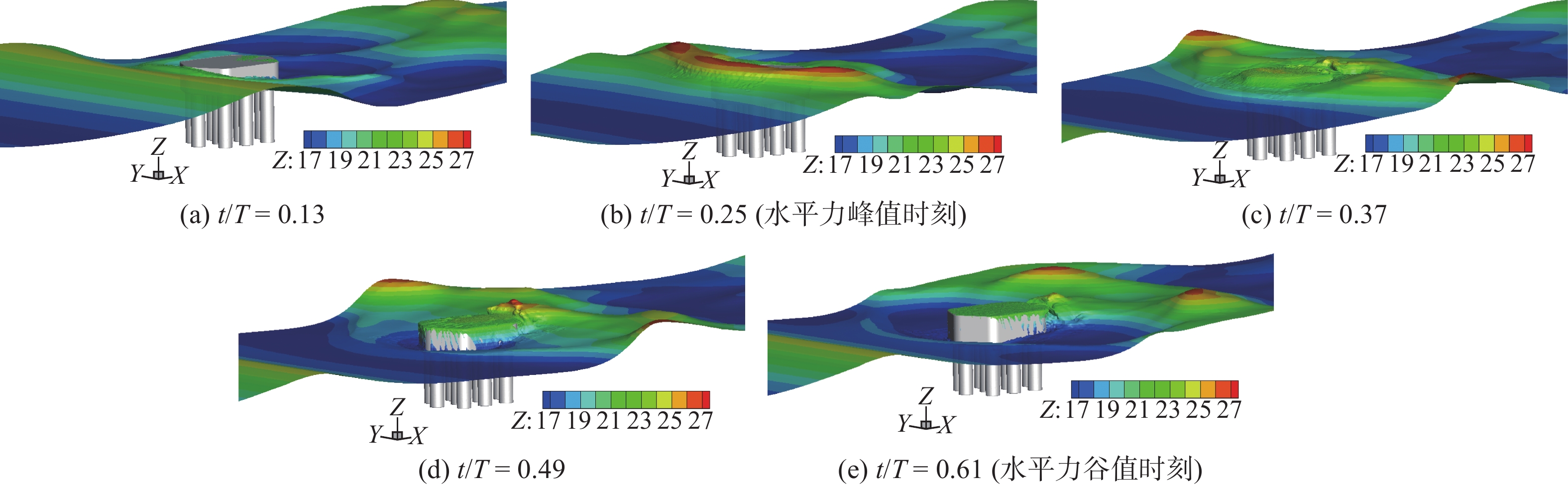
图11~13给出了3种工况下,水平荷载由峰值至谷值各时刻波浪形态历程。由图11可见,当
$ {C_{\text{s}}} $ =1.00时,越浪现象明显,波浪传播过程中较完整,未被击碎,承台对波浪的阻挡效应较弱。正向水平力达到峰值前,浪潮头已越过结构,波浪拍击效应较弱,承台整体处于波浪液面以下。由此可见,此时水平力峰值来自浪流联合作用。波浪完全越过承台后,在尾流区产生明显的绕射波浪,与正向波浪汇聚形成水流向上脉冲现象,反向波浪与正向波浪合力作用在承台底面,产生了竖向浮托力二次峰值。由图12可见,Cs=0.55时,波浪没有完全越过承台结构,当波峰冲击承台正面时,形成正向水平力峰值;波浪完全越过承台后,发展出紊乱无序的绕射波浪,导致负向水平力的波动变化。由图13可见,$ {C_{\text{s}}} $ =0时,波浪与承台正向有明显的冲击拍打现象,说明水平力峰值持续时间极短。此外,观察图13(e)可知,${C_{\text{s}}}$ =0时,波浪越过承台后,尾流区没有明显的绕射波浪,以至于承台的反向冲击效应不明显。对比3种工况波浪形态时程图,可以总结出高桩承台基础的波浪荷载形成机理:(1)当淹没系数较大时,波浪的拍击效应较弱,承台压力峰值主要来自浪流联合作用;(2)随着水位降低,水平力峰值的脉冲效应逐渐明显,由于承台淹没系数的降低,水流对承台作用降低,荷载以波浪拍击力为主;(3)结构尾流区会形成绕射波浪,且绕射效应随淹没系数增大而增强,绕射波浪会产生负向水平力和负向浮托力;(4)随着淹没水位降低,直至波面直接与群桩接触,波浪传播中被群桩干扰阻碍形成破碎波,致使群桩总力、单桩水平力的时程变化波动剧烈。
5. 波流作用下桩-承台压力分布特性
为研究承台在不同工况波浪作用下的压力分布,定义平均压力系数及承台脉动压力系数:
$$ {\overline C _{{\text{p}}i}} = {{2{{\overline P }_i}}}/({{\rho g\overline H }}) $$ (15) $$ {\mathop C\limits^ \wedge } _{{\text{p}}i}= {{2{{\mathop P\limits^ \wedge }_i}}}/({{\rho g\overline H }}) $$ (16) 式中:
$ {\overline C _{{\text{p}}i}} $ 、${\mathop C\limits^ \wedge }_{{\text{p}}i}$ 为承台及桩基平均压力系数和脉动压力系数;$ {\overline P _i} $ 、${\mathop P\limits^ \wedge } _i$ 为承台及桩基i测点上,若干周期内的压强平均值和压强均方根误差。图14给出了不同工况下的承台、桩基平均压力分布三维视图(下)和承台俯视图(上)。可见,承台及桩基平均压力分布明显与初始水位有关,即结构位置所处水位以下越深,所受平均水压越大。同深度迎波面桩基压力明显大于背波面。进一步观察发现,在同高度范围内,承台侧面转角处平均压力明显低于相邻竖侧面。结合图11~13分析可知,波浪传播时会被承台阻碍形成“劈波效应”,波浪沿承台转角处分散传播,导致转角处受波浪冲击效应低于周围侧面。图14(c)显示转角附近平均压力趋于0,结合图13(b)可知:随着淹没系数的降低,承台“劈波效应”更加明显。
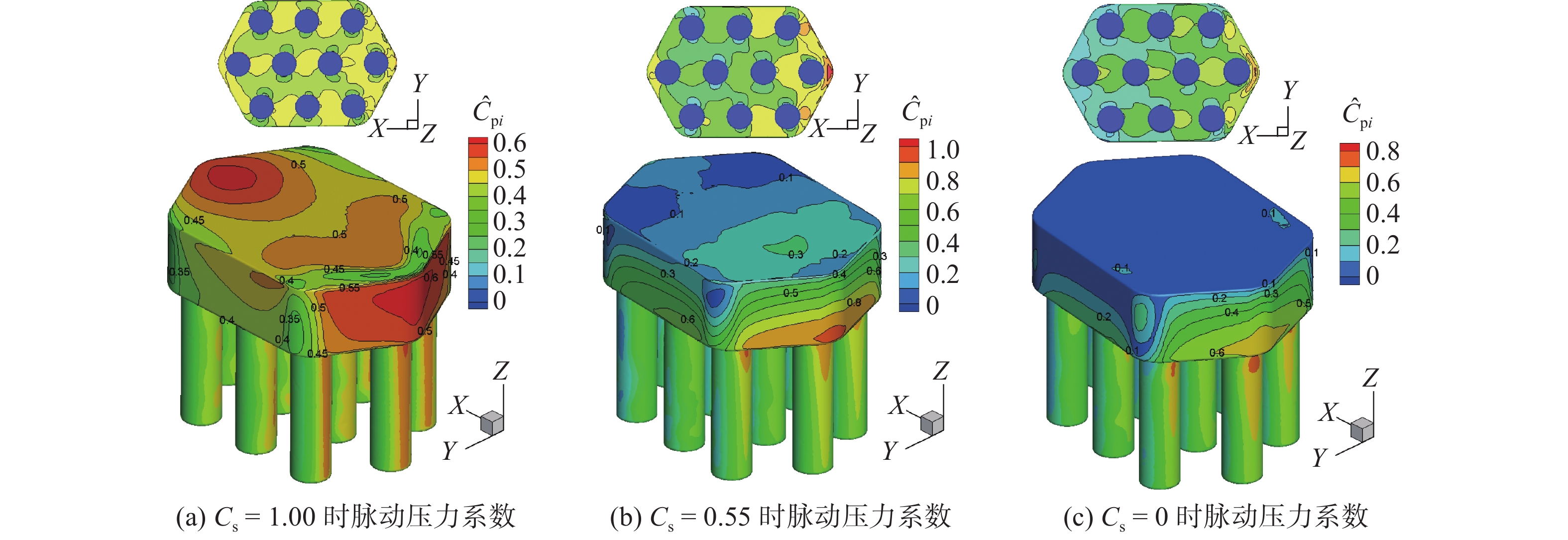
图15显示了承台及桩基表面压力波动情况。当
$ {C_{\text{s}}} $ =1.00时,承台前迎波面和顶面尾部两处有明显的脉动压力系数极值区,随着淹没系数的降低,脉动压力系数极值区域不断缩小直至消失,因为迎波面压力波动是由波浪周期性正面冲击承台形成的。结合图11可知,$ {C_{\text{s}}} $ =1.00时顶面压力波动是由绕射波浪与正向波浪汇聚冲击而形成。随着淹没系数的降低,越浪效应减弱,致使顶面压力波动减弱。$ {C_{\text{s}}} $ =0时,波浪未越过承台结构,拍击承台正面后被分离成破碎波向两侧传播,承台顶面未受水压作用,因此顶面压力脉动系数几乎无变化。继续观察承台底面脉动压力系数分布,可以看出几种工况下,承台底面沿X方向桩列和桩间脉动效应差异明显,即随着淹没系数的增加,前后方向脉动压力系数存在明显梯度,桩列的“阻挡效应”和“劈波效应”也显著增强。6. 结 语
为研究高桩承台基础在波流作用下的荷载时程特性及压力分布规律,采用RANS方法对某跨海大桥高桩承台基础进行数值模拟研究,得到以下结论:
(1)承台水平力随淹没系数增加而增加,承台浮托力、群桩水平力随淹没系数增加而降低。
(2)群桩正向总力最大时,迎波方向的边列最后排桩基受力最大;群桩负向总力最大时,迎波方向中间列桩存在明显的越靠后排贡献系数越大的规律,且中间列最后排桩在群桩中受力最大。
(3)淹没系数较大时,承台压力峰值主要来自于浪流共同作用,结构尾流区会形成绕射波浪,绕射波浪会产生负向水平力和负向浮托力。随着淹没系数的降低,承台对波浪的“劈波效应”增强,水平力峰值的脉冲效应明显,水流作用影响减弱。波浪传播中被群桩干扰阻碍形成破碎波,致使群桩总力、单桩水平力的时程变化波动剧烈。
(4)由于“劈波效应”,使得承台棱角部分平均压力低于附近侧面。初始静水面与承台顶平齐时,承台正前方和顶部后方会产生波动极值区域,并随着静水位降低而逐渐减小并消失。
-
表 1 波浪要素及计算工况
Table 1 Wave elements and working conditions
淹没系数 静水深度/m 波高/m 周期/s 波长/m 静水流速/(m·s−1) Cs=1.00 22.30 6.9 8.3 96 3.64 Cs=0.55 18.93 Cs=0 14.80 表 2 不同网格方案参数
Table 2 Parameters of different grid schemes
方案 最大网格尺寸/m 单元数/个 Z/Y向网格 X向网格 承台-桩表面网格 网格方案1 4.0 6.0 4.00 172 785 网格方案2 2.0 6.0 2.00 297 177 网格方案3 2.0 6.0 1.00 346 513 网格方案4 1.0 3.0 0.50 1 015 335 网格方案5 1.0 3.0 0.25 2 005 582 网格方案6 0.5 1.0 0.10 5 402 545 表 3
$ {C_{\text{s}}} $ =1.00计算结果对比Table 3 Comparison of calculation results (
$ {C_{\text{s}}} $ =1.00)单位:kN 方案 承台水平力 承台浮托力 桩基最大力 单桩最大力 网格方案1 7 296.22 3 154.68 5 698.01 741.48(Z8) 网格方案2 7 250.34 3 472.13 5 445.38 705.38(Z4) 网格方案3 6 993.28 3 766.94 4 876.31 540.78(Z10) 网格方案4 7 006.78 3 685.23 4 638.88 546.02(Z10) 网格方案5 7 182.15 4 206.10 4 461.20 556.40(Z3) 网格方案6 7 173.45 4 216.13 4 213.40 543.23(Z3) 试验数值 6 768.5 4 616.1 4 393.7 507.4(Z3) -
[1] 方庆贺. 跨海近岸桥梁极端波浪作用研究[D]. 哈尔滨: 哈尔滨工业大学, 2012. FANG Qinghe. Study on extreme wave loads of coastal highway bridges[D]. Harbin: Harbin Institute of Technology, 2012. (in Chinese)
[2] 项海帆. 21世纪世界桥梁工程的展望[J]. 土木工程学报,2000,33(3):1-6 XIANG Haifan. Prospect of world’s bridge projects in 21st century[J]. China Civil Engineering Journal, 2000, 33(3): 1-6. (in Chinese)
[3] 黄雯, 冯谊武, 张海龙. 波浪作用下的群桩受力及优化布置[J]. 桥梁建设,2016,46(3):51-56 HUANG Wen, FENG Yiwu, ZHANG Hailong. Mechanical properties and optimal arrangement of group piles acted by wave forces[J]. Bridge Construction, 2016, 46(3): 51-56. (in Chinese)
[4] 房忱, 李永乐, 秦顺全, 等. 中、美、英规范关于跨海桥梁桩基波浪力的对比[J]. 桥梁建设,2016,46(6):94-99 FANG Chen, LI Yongle, QIN Shunquan, et al. Comparison of wave forces of pile foundations for sea-crossing bridges provided in Chinese, American and British codes[J]. Bridge Construction, 2016, 46(6): 94-99. (in Chinese)
[5] MORISON J R, JOHNSON J W, SCHAAF S A. The force exerted by surface waves on piles[J]. Journal of Petroleum Technology, 1950, 2(5): 149-154. doi: 10.2118/950149-G
[6] WEI K, YUAN W C, BOUAANANI N. Experimental and numerical assessment of the three-dimensional modal dynamic response of bridge pile foundations submerged in water[J]. Journal of Bridge Engineering, 2013, 18(10): 1032-1041. doi: 10.1061/(ASCE)BE.1943-5592.0000442
[7] MACCAMY R C, FUCHS R A. Wave forces on pliles: a diffraction theory[R]. Corps of Engineers Washington DC Beach Erosin Board, Ojio: Us Army Coastal Engineering Research Center, 1954.
[8] BHATTA D D, RAHMAN M. On scattering and radiation problem for a cylinder in water of finite depth[J]. International Journal of Engineering Science, 2003, 41(9): 931-967. doi: 10.1016/S0020-7225(02)00381-6
[9] 杜修力, 赵娟, 赵密. 大直径深水圆柱结构动水压力的时域算法[J]. 土木工程学报,2012,45(增刊1):316-320 DU Xiuli, ZHAO Juan, ZHAO Mi. A time-domain method for the hydrodynamic pressure on deep-water cylindrical structure with large diameter[J]. China Civil Engineering Journal, 2012, 45(Suppl1): 316-320. (in Chinese)
[10] 张胡, 刘清君, 王登婷. 大尺度结构波浪力计算研究[J]. 水道港口,2018,39(2):151-156, 187 ZHANG Hu, LIU Qingjun, WANG Dengting. Research on calculation of wave forces acting on the large scale structure[J]. Journal of Waterway and Harbor, 2018, 39(2): 151-156, 187. (in Chinese)
[11] 邓莎莎, 沈火明, 刘浪, 等. 基于绕射理论的大尺度桥墩波浪力计算方法[J]. 西南交通大学学报,2018,53(2):266-271 DENG Shasha, SHEN Huoming, LIU Lang, et al. Research of calculation method for wave forces acting on large-scale bridge piers based on diffraction theory[J]. Journal of Southwest Jiaotong University, 2018, 53(2): 266-271. (in Chinese)
[12] 兰雅梅. 桩基结构物的波-流作用力研究[D]. 上海: 上海交通大学, 2006. LAN Yamei. Study on hydrodynamic loads on piled structures in wave-current combination[D]. Shanghai: Shanghai Jiao Tong University, 2006. (in Chinese)
[13] 魏凯, 周聪, 徐博. 跨海桥梁高桩承台波浪冲击荷载概率模型[J]. 工程力学,2020,37(6):216-224 WEI Kai, ZHOU Cong, XU Bo. Probability model of wave impact load on the elevated pile cap for sea-crossing bridges[J]. Engineering Mechanics, 2020, 37(6): 216-224. (in Chinese)
[14] 仇正中, 赵东梁. 中马友谊大桥主桥承台波浪荷载数值模拟研究[J]. 施工技术,2019,48(5):5-8 QIU Zhengzhong, ZHAO Dongliang. Study on numerical simulation of wave load on main bridge foundation cap for China and Maldives friendship bridge[J]. Construction Technology, 2019, 48(5): 5-8. (in Chinese)
[15] 刘正浩, 万德成. 波流作用下海上固定式风机基础的水动力性能数值模拟[J]. 江苏科技大学学报(自然科学版),2017,31(5):555-560, 566 LIU Zhenghao, WAN Decheng. Numerical study of hydrodynamic performance of wind turbine foundation under wave-current combinations[J]. Journal of Jiangsu University of Science and Technology (Natural Science Edition), 2017, 31(5): 555-560, 566. (in Chinese)
[16] 董伟良, 诸裕良, 胡金春, 等. 跨海桥梁大尺寸承台波浪力数值模拟研究[J]. 水道港口,2020,41(1):50-57 DONG Weiliang, ZHU Yuliang, HU Jinchun, et al. Numerical simulation study of wave load on large-size cap of cross-sea bridge[J]. Journal of Waterway and Harbor, 2020, 41(1): 50-57. (in Chinese)
[17] 金小凯, 陈锦剑, 廖晨聪. 波浪荷载对单桩承载力影响的水槽模拟试验研究[J]. 上海交通大学学报,2021,55(4):365-371 JIN Xiaokai, CHEN Jinjian, LIAO Chencong. Wave flume simulation experiment on influence of wave load on bearing capacity of monopile[J]. Journal of Shanghai Jiao Tong University, 2021, 55(4): 365-371. (in Chinese)
[18] 徐博, 魏凯. 基于RANS的跨海桥梁高桩承台波浪作用数值模拟[J]. 铁道标准设计,2019,63(12):79-84 XU Bo, WEI Kai. Numerical simulation of wave forces on elevated pile cap of sea-crossing bridges based on RANS[J]. Railway Standard Design, 2019, 63(12): 79-84. (in Chinese)
[19] 刘桦, 王本龙, 薛雷平, 等. 桩基承台结构的波流力研究进展[J]. 应用数学和力学,2013,34(10):1098-1109 LIU Hua, WANG Benlong, XUE Leiping, et al. Recent progress in wave-current loads on foundation structure with piles and cap[J]. Applied Mathematics and Mechanics, 2013, 34(10): 1098-1109. (in Chinese)
[20] 张洪翔. 波浪-流联合作用下结构-海床耦合系统的动力响应分析[D]. 南京: 南京航空航天大学, 2019. ZHANG Hongxiang. Dynamic response analysis of structure-seabed coupled system under wave-current[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2019. (in Chinese)
-
期刊类型引用(2)
1. 刘宏图. 大型跨海桥梁桩基强波浪动力响应特征研究. 铁道建筑技术. 2024(05): 112-116 .  百度学术
百度学术
2. 郑仲园,梁钰儿. 佛山市甘竹水文站迁站重建工程探讨. 吉林水利. 2024(09): 69-73 .  百度学术
百度学术
其他类型引用(0)



 Email Alerts
Email Alerts RSS
RSS
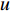
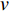
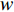
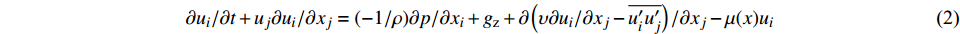
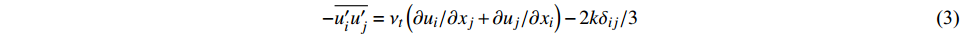
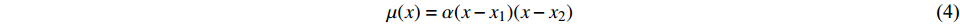
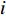
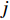
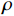
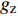
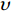
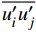
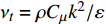
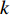
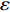
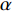

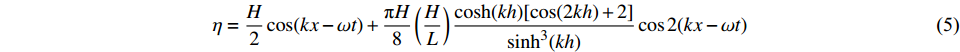
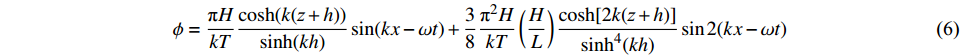
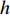

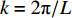
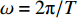
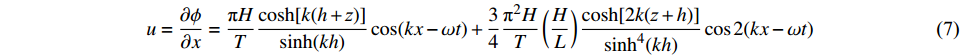
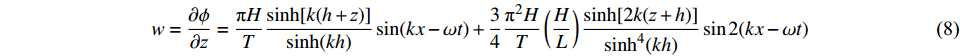

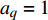
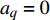
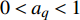
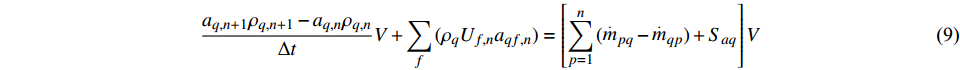
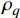
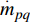
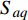
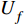
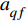
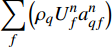
 下载:
下载: